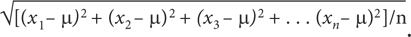Приложение к главе 2
Данные для графического отображения дефектов принтера
Формула для дисперсии и среднеквадратического отклонения
Дисперсия и среднеквадратическое отклонение — самые распространенные статистические механизмы для измерения и описания разброса того или иного распределения. Дисперсия, которая часто обозначается символом σ2, вычисляется путем определения, насколько далеко от среднего значения расположены наблюдения в рамках того или иного распределения. Однако фишка в данном случае состоит в том, что расстояние (разница) между каждым наблюдением и средним значением возводится в квадрат; сумма таких составляющих, возведенных в квадрат, затем делится на количество наблюдений.
А именно:
Для любой совокупности из n наблюдений x1, x2, x3 … xn со средним значением μ
Дисперсия = σ2 = [(x1 –μ)2 + (x2 – μ)2 + (x3 – μ)2 + … (xn – μ)2] / n
Поскольку разница между каждым членом и средним значением возводится в квадрат, формула для вычисления дисперсии присваивает определенный вес наблюдениям, которые расположены вдали от среднего значения (то есть «отщепенцам»), как показано в приведенной ниже таблице роста учащихся.


* Абсолютное значение — это расстояние между двумя числами, независимо от знака разности между ними, то есть это значение всегда положительное. В данном случае оно представляет собой разницу в дюймах между ростом конкретного человека и средним значением.
Средний рост обеих групп учащихся составляет 70 дюймов. Суммы абсолютных отклонений от среднего значения в обеих группах также одинаковы — 14 дюймов. По этому показателю разброса указанные два распределения идентичны. Однако дисперсия для группы 2 оказалась выше из-за веса, присвоенного в формуле дисперсии значениям, которые расположены особенно далеко от среднего значения (в нашем случае эти значения относятся к Сахар и Нарцисо).
Дисперсия сама по себе редко используется в качестве описательной статистики. В наибольшей степени она полезна как один из шагов в направлении вычисления среднеквадратического (стандартного) отклонения интересующего нас распределения, которое, как описательная статистика, является более интуитивно понятным инструментом.
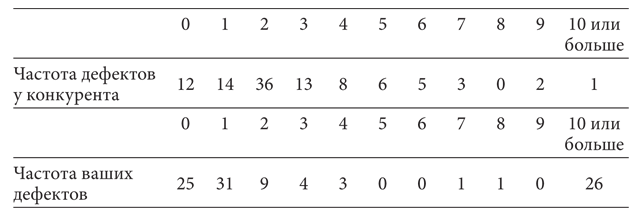
Среднеквадратическое отклонение для совокупности наблюдений представляет собой корень квадратный из дисперсии:
Для любой совокупности из n наблюдений x1, x2, x3 … xn со средним значением µ среднеквадратическое отклонение = σ = корню квадратному из этой величины =