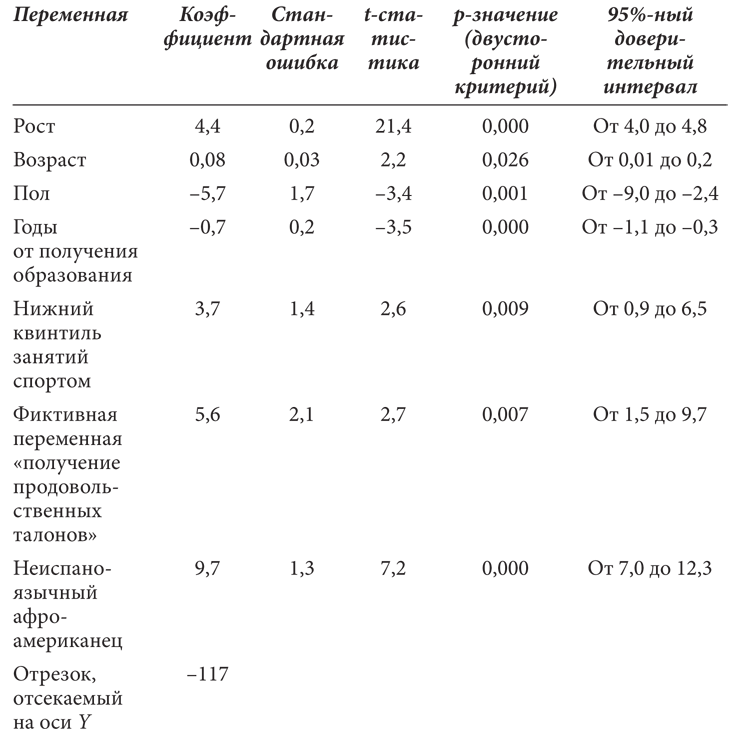
Приложение к главе 11
t-распределение
Жизнь несколько усложняется при выполнении регрессионного анализа (или других видов статистического вывода) с малой выборкой данных. Допустим, нам нужно проанализировать зависимость между весом и ростом на основе выборки, состоящей всего из 25 взрослых, вместо того чтобы использовать огромный набор данных, как в исследовании Americans’ Changing Lives. Логика подсказывает, что надо с меньшей уверенностью обобщать полученные результаты на все взрослое население, если выборка состоит не из 3000 взрослых, а лишь из 25. Одно из положений, которые неоднократно подчеркивались в этой книге, заключается в том, что меньшие выборки, как правило, порождают больший разброс исходов. Выборка из 25 взрослых по-прежнему обеспечивает значимые результаты, как обеспечивала бы выборка из 10 и даже 5 человек, но насколько значимыми они являются?
На этот вопрос ответит t-распределение. При анализе зависимости между ростом и весом для нескольких выборок из 25 взрослых уже нельзя исходить из того, что разные коэффициенты регрессии, которые мы получаем, будут распределены по нормальному закону вблизи «истинного» коэффициента регрессии для взрослого населения в целом. Они по-прежнему будут распределяться вблизи «истинного» коэффициента для взрослого населения в целом, но формой этого распределения уже не будет хорошо нам знакомая колоколообразная кривая нормального распределения. Вместо этого мы должны предположить, что многие выборки, состоящие лишь из 25 взрослых, будут порождать больший разброс вблизи истинного коэффициента совокупности и, следовательно, это распределение будет с «более толстыми хвостами». А многие выборки из 10 взрослых будут порождать еще больший разброс и, соответственно, распределение с еще более толстыми хвостами. По сути, t-распределение представляет собой некую совокупность, или «семейство», функций плотности вероятности, которые варьируются в зависимости от величины выборки. В частности, чем больше данных содержится в выборке, тем больше «степеней свободы» у нас имеется при определении подходящего распределения, которое служит нам эталоном для оценки результатов. Если вы решите изучать более продвинутый курс статистики, то узнаете, как именно вычисляются степени свободы; пока же можем считать, что они примерно равны количеству наблюдений в выборке. Например, регрессионный анализ с выборкой, размер которой составляет 10, и с единственной объясняющей переменной, имеет 9 степеней свободы. Чем больше степеней свободы, тем больше уверенность, что выборка представляет истинную совокупность, и тем «плотнее» будет распределение, как следует из приведенной ниже диаграммы.
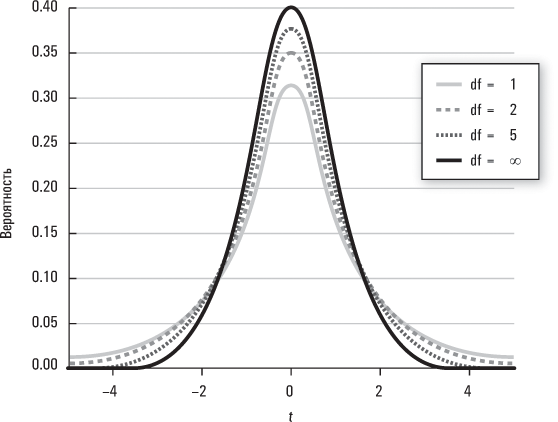
Когда число степеней свободы увеличивается, t-распределение сходится к нормальному распределению. Именно поэтому при работе с большими совокупностями данных вы можете использовать для соответствующих вычислений нормальное распределение.
t-распределение лишь добавляет определенные нюансы в тот же процесс статистического вывода, который мы неоднократно использовали в этой книге. Мы по-прежнему формулируем нулевую гипотезу, а затем проверяем ее на наблюдаемых нами данных. Если эти данные крайне маловероятны в случае правильности нулевой гипотезы, то она отвергается. Единственное, что изменяется при использовании t-распределения, — это основные вероятности для оценивания наблюдаемых исходов. Чем «толще» хвост у конкретного распределения вероятностей (например, t-распределение для восьми степеней свободы), тем больший разброс следует ожидать в наблюдаемых данных и, следовательно, тем меньше уверенность в правильности отказа от нулевой гипотезы.
Допустим, мы решаем уравнение регрессии и, согласно нулевой гипотезе, коэффициент при какой-то конкретной переменной равняется нулю. После того как мы получим результаты вычислений, мы могли бы рассчитать t-статистику, которая представляет собой отношение наблюдаемого коэффициента к стандартной ошибке для этого коэффициента. Эта t-статистика затем оценивается с точки зрения величины выборки данных, для которой подходит t-распределение (поскольку именно это в значительной мере определяет число степеней свободы). Когда t-статистика достаточно велика, то есть наблюдаемый коэффициент далек от того, что предсказывает нулевая гипотеза, мы можем отвергнуть нулевую гипотезу на некотором уровне статистической значимости. Опять-таки это тот же самый базовый процесс статистического вывода, с которым мы неоднократно сталкивались в этой книге.
Чем меньше степеней свободы (и, следовательно, чем «толще» хвосты у соответствующего t-распределения), тем больше должна быть t-статистика, чтобы мы могли отвергнуть нулевую гипотезу на некотором заданном уровне статистической значимости. Если бы в описанном выше гипотетическом примере регрессии было четыре степени свободы, то нам понадобилось бы, чтобы t-статистика была не менее 2,13: только в этом случае мы могли бы отвергнуть нулевую гипотезу на доверительном уровне 0,05 (при использовании одностороннего критерия).
Если бы у нас было 20 000 степеней свободы (что вполне позволяет использовать нормальное распределение), то для того чтобы отвергнуть нулевую гипотезу на доверительном уровне 0,05 (при использовании того же одностороннего критерия), необходимо, чтобы t-статистика равнялась всего 1,65.
Уравнение регрессии для веса