9

Статистические выводы

Почему моему преподавателю статистики казалось, что я пытаюсь его обмануть

Весной, будучи уже в старших классах колледжа, я решил прослушать курс лекций по статистике. Вообще говоря, в то время я не испытывал особой любви ни к ней, ни к любым другим наукам, базирующимся на математике, но пообещал отцу, что прослушаю этот курс лекций с условием, что мне разрешат на десять дней поехать в СССР. Короче говоря, это был взаимовыгодный обмен, причем, как оказалось, статистика увлекла меня гораздо больше, чем я предполагал, к тому же мне удалось побывать в СССР весной 1988 года. Кто же тогда знал, что эта страна буквально через несколько лет расстанется со своим коммунистическим прошлым!

В действительности эта история имеет непосредственное отношение к материалу данной главы: дело в том, что в то время я не уделял изучению статистики должного внимания. Помимо всего прочего, я писал тогда дипломную работу, и до ее сдачи у меня оставалось не так уж много времени. По мере прохождения курса статистики мы периодически сдавали промежуточные экзамены, многие из которых я либо проваливал, либо попросту игнорировал. К середине семестра багаж знаний, полученных мною по данной дисциплине, был настолько скудным, что я мог рассчитывать исключительно на чудо. Но буквально за несколько недель до окончания семестра произошли два важных события. Во-первых, я дописал дипломную работу, в результате чего у меня появилось довольно много свободного времени. И во-вторых, осознал, что статистика не такая уж сложная наука, как мне казалось до этого. Я начал усиленно штудировать учебники по статистике, наверстывая упущенный материал. Итоговый экзамен по статистике я сдал на отлично.

Именно тогда преподаватель статистики (к сожалению, я забыл его имя) вызвал меня к себе в кабинет. Не помню точно, что он мне сказал, но это было нечто вроде: «Вы добились потрясающих успехов по сравнению с серединой семестра». Однако его слова звучали отнюдь не как похвала моим достижениям. Напротив, в них мне послышалось скрытое обвинение в том, что во время сдачи экзамена я пользовался шпаргалками. Учитель не мог поверить в то, что студент, так «мелко плававший» на промежуточных экзаменах, способен на столь мощный рывок к концу семестра. Тогда мне было очень обидно, что меня подозревают в обмане, но со временем я понял этого человека и нисколько не осуждаю. Практически по всем предметам, изучаемым в колледже, наблюдается высокая степень корреляции между результатами, которые студенты демонстрируют на промежуточных и итоговых экзаменах. Очень маловероятно, что студент, получивший на промежуточных экзаменах оценку ниже средней, покажет блестящий результат во время сдачи итоговых экзаменов.

Я объяснил преподавателю, что, завершив написание дипломной работы, решил со всей серьезностью отнестись к изучению курса статистики (для этого мне понадобилось всего лишь читать рекомендованные им главы учебника и своевременно выполнять домашние задания). Мне показалось, что я его убедил, хотя его подозрение в том, что во время экзамена я пользовался шпаргалками (пусть даже не высказанное вслух), по-прежнему не давало мне покоя.

Хотите верьте, хотите нет, но этот случай воплощает в себе многое из того, что вам нужно знать о статистическом выводе, в том числе о его достоинствах и потенциальных недостатках. Статистика не может ничего утверждать с определенностью. Напротив, сила статистического вывода проистекает из наблюдения некой картины или исхода и последующего использования теории вероятностей для получения его (ее) самого вероятного объяснения. Допустим, в ваш город прибыл большой любитель азартных игр и предлагает вам пари: он выигрывает 1000 долларов, если в результате подбрасывания игральной кости выпадет шестерка; вы выигрываете 500 долларов, если выпадет любое другое число, — очень выгодный, на ваш взгляд, вариант. Затем в результате десяти подбрасываний игральной кости у него десять раз подряд выпадает шестерка. Вам не остается ничего другого, как уплатить 10 000 долларов.

Одно возможное объяснение этого феномена — необычайное везение вашего визави. Альтернативное объяснение — обман с его стороны. Вероятность того, что в ходе десяти подбрасываний «правильной» игральной кости десять раз подряд выпадет шестерка, равняется примерно 1 шансу из 60 миллионов. Вы не можете доказать, что ваш партнер смошенничал, но вы должны по крайней мере проверить, все ли в порядке с игральной костью.

Разумеется, самое вероятное (правдоподобное) объяснение не всегда окажется правильным. Порой действительно случается то, что не должно было бы случиться. В Линду Купер из штата Южная Каролина четыре раза попадала молния. (По оценкам Федеральной службы чрезвычайных ситуаций, вероятность однократного попадания молнии в человека составляет 1 шанс из 600 000.) Страховая компания Линды Купер не может отказать ей в выплате компенсации лишь на основании того, что полученные ею травмы в результате попаданий молнии статистически невероятны. Что касается моего выпускного экзамена по статистике, то у преподавателя были причины подозревать меня в мошенничестве, поскольку он увидел крайне маловероятную картину (именно так следователи выявляют манипуляции с результатами стандартизованных тестов, а Комиссия по ценным бумагам и биржам — инсайдерские торговые операции с ценными бумагами). Но маловероятная картина остается просто маловероятной картиной, если наши подозрения не подтверждаются какими-либо дополнительными свидетельствами. Ниже мы обсудим ошибки, которые могут возникнуть в случаях, когда вероятность направляет нас по ложному пути.

На этом этапе нам следует уяснить, что статистический вывод использует данные для получения ответов на важные вопросы. Эффективно ли новое лекарство, предназначенное для лечения заболеваний сердца? Являются ли мобильные телефоны причиной развития раковых опухолей мозга? Обратите внимание: я вовсе не утверждаю, что статистика может ответить на такие вопросы однозначно. Статистический вывод говорит лишь о том, что вполне вероятно, а что — маловероятно или даже крайне невероятно. Исследователи не могут утверждать, что новое лекарство, предназначенное для лечения заболеваний сердца, действительно эффективно, даже располагая результатами его надлежащим образом проведенных клинических испытаний. В конце концов, вполне возможно, что при лечении пациентов в подопытной и контрольной группах появится случайное отклонение, никак не связанное с новым препаратом. То, что у 53 из 100 пациентов, принимающих это лекарство, наметилось существенное улучшение состояния здоровья, тогда как в группе пациентов, принимающих плацебо, такая картина наблюдается у 49 пациентов из 100, не дает нам права безапелляционно заявлять об эффективности нового препарата. Такой исход можно объяснить случайным отклонением между двумя группами пациентов, а вовсе не действием нового лекарства.

Допустим, однако, что у 91 из 100 пациентов, принимающих новое лекарство, произошло существенное улучшение состояния здоровья, тогда как в контрольной группе здоровье значительно улучшилось только у 49 из 100 пациентов. Конечно, и на сей раз не исключено, что столь впечатляющий результат никак не связан с приемом нового препарата; возможно, пациентам в подопытной группе просто улыбнулась удача (а может, все дело в их жизнелюбии и оптимизме). Однако в данном случае такое объяснение из разряда маловероятных. На формальном языке статистического вывода, исследователи, скорее всего, заключили бы следующее. 1) Если бы экспериментальное лекарство никак не сказывалось на состоянии пациентов, то столь сильное отклонение в исходах между теми, кто его принимает, и теми, кто принимает плацебо, явилось бы большой редкостью. 2) Поэтому крайне маловероятно, что препарат не оказывает положительного воздействия на состояние пациентов. 3) Альтернативное — и более вероятное — объяснение полученной нами картины заключается в том, что экспериментальное лекарство оказывает положительный эффект.

Статистический вывод — это процесс, посредством которого данные позволяют нам делать обоснованные заключения. Именно в этом его достоинство! Задача статистики не в выполнении огромного множества строгих математических расчетов, а в том, чтобы помочь нам лучше разобраться в важных социальных (и не только) явлениях. Статистический вывод — это, по сути, союз двух уже обсуждавшихся нами концепций: данных и вероятности (с определенной помощью со стороны центральной предельной теоремы). В настоящей главе я воспользовался одним значимым методологическим упрощением: все приведенные мною примеры предполагают, что мы используем большую, надлежащим образом сформированную выборку. Это предположение означает возможность применения центральной предельной теоремы и то, что среднее значение и среднеквадратическое отклонение для любой выборки будет примерно таким же, как среднее значение и среднеквадратическое отклонение для совокупности, из которой она сформирована. Оба допущения делают наши расчеты проще.

Статистический вывод не зависит от этого упрощающего предположения, но систе­матизи­рованные методологические уточнения, позволяющие работать с малыми выборками или неполными данными, зачастую лишь препятствуют пониманию общей картины. Цель в данном случае — сделать так, чтобы читатель смог оценить важность и богатые возможности статистического вывода, а также механизм его действия. После того как вы уясните это, можно переходить на более высокий уровень сложности.

Одним из самых распространенных инструментов в статистическом выводе является проверка гипотез. Фактически я уже знакомил вас с этой концепцией — правда, не прибегая к использованию заумной терминологии. Как указывалось выше, сама по себе статистика не может ничего доказать; вместо этого мы применяем статистический вывод, чтобы принимать или отвергать объяснения на основе их вероятности. Точнее говоря, любой статистический вывод начинается с подразумеваемой или явно сформулированной основной (так называемой нулевой) гипотезы. Это наша начальная гипотеза, которая будет отвергнута или принята исходя из последующего статистического анализа. Если мы отвергаем нулевую гипотезу, то, как правило, принимаем какую-то альтернативную гипотезу, которая в большей степени соответствует наблюдаемым нами данным. Например, исходным предположением (или основной гипотезой) в суде является невиновность подсудимого (так называемая презумпция невиновности). Задача обвинения — убедить судью или присяжных в необходимости отклонить это предположение и принять альтернативную гипотезу, что подсудимый виновен. С точки зрения логики альтернативная гипотеза представляет собой заключение, которое должно быть истинным, если мы можем опровергнуть основную гипотезу. Рассмотрим несколько примеров.

Нулевая гипотеза: новый экспериментальный препарат не более эффективен для профилактики малярии, чем плацебо.

Альтернативная гипотеза: новый экспериментальный препарат способствует профилактике малярии.

Данные: члены случайным образом сформированной группы будут принимать новое экспериментальное лекарство, а контрольная группа будет принимать плацебо. По окончании определенного периода в группе, принимавшей новый препарат, было зафиксировано значительно меньше случаев заболевания малярией, чем в контрольной группе. Это было бы крайне маловероятно, если бы новое экспериментальное лекарство не оказывало медицинского воздействия. Таким образом, мы отвергаем нулевую гипотезу, что новый препарат не имеет медицинских последствий (конечно же, помимо известного эффекта плацебо), и принимаем логическую альтернативу, то есть альтернативную гипотезу: новое экспериментальное лекарство способствует профилактике малярии.

Такой методологический подход достаточно необычен, поэтому приведу еще один пример. Опять же обратите внимание, что нулевая и альтернативная гипотезы логически дополняют друг друга. Если одна оказывается истинной, то другая таковой не является. Или если мы отвергаем одну гипотезу, то должны принять другую. Теперь еще один пример.

Нулевая гипотеза: лечение заключенных от наркозависимости не снижает вероятности их повторного ареста после выхода из тюрьмы.

Альтернативная гипотеза: лечение заключенных от наркозависимости снижает вероятность их повторного ареста после выхода из тюрьмы.

Данные (гипотетические): заключенных случайным образом разделили на две группы, «подопытная» группа проходила курс лечения от наркоза­висимости, а контрольная группа — нет. Через пять лет оказалось, что вероятность повторного ареста членов обеих групп примерно одинакова. То есть в этом случае мы не можем отвергнуть нулевую гипотезу. Эти данные не дают нам повода отклонить исходное предположение о том, что лечение заключенных от наркозависимости не спасает их от повторного попадания за решетку.

Это может показаться нелогичным, но исследователи часто формулируют нулевую гипотезу в надежде, что им удастся отвергнуть ее. В обоих приведенных выше примерах «успех» исследования (создание нового лекарства для профилактики малярии или снижение вероятности повторного ареста) подразумевал отказ от нулевой гипотезы. Сделать это на основе имеющихся данных удалось лишь в одном из случаев (лекарство для профилактики малярии).

В зале суда порогом для отмены презумпции невиновности является качественная оценка, что подсудимый «виновен ввиду разумных оснований для сомнения». Что именно означает в каждом конкретном случае такая формулировка, решает судья или присяжные заседатели. Статистика использует аналогичную основополагающую идею, но формула «виновен ввиду разумных оснований для сомнения» определяется не качественно, а количественно. Исследователи обычно спрашивают: если нулевая гипотеза истинна, то какова вероятность того, что мы наблюдаем такую картину данных по чистой случайности? Если мы воспользуемся приведенным в начале главы примером, то ученые-медики могут спросить: если это экспериментальное лекарство не способствует излечению сердечно-сосудистых заболеваний (нулевая гипотеза), то какова вероятность того, что состояние здоровья 91 из 100 пациентов, принимавших его, улучшилось, если учесть, что улучшение состояния здоровья было отмечено лишь у 49 из 100 пациентов, принимавших плацебо? Если имеющиеся в нашем распоряжении данные свидетельствуют о крайней маловероятности нулевой гипотезы (как в примере с экспериментальным лекарством), то мы должны отвергнуть ее и принять альтернативную гипотезу (о том, что экспериментальное лекарство способствует излечению от сердечно-сосудистых заболеваний).

С учетом этого давайте еще раз вернемся к скандалу, вызванному махинациями с результатами стандартизированных тестов в Атланте, о которых мы неоднократно упоминали в этой книге. Эти результаты привлекли к себе внимание контролирующих органов из-за высокого количества исправлений неправильных ответов на правильные. Понятно, что учащиеся, которым приходится сдавать стандартизованные тесты, время от времени исправляют свои ответы. Не исключено и то, что каким-то группам учащихся, прибегающих к таким исправлениям, особенно везет — и это вовсе не связано с какими-либо махинациями. Именно поэтому основная гипотеза сводится к тому, что результаты сдачи стандартизированных тестов в любом конкретном учебном округе правильны (с точки зрения закона) и что любые исправления — не более чем продукт случайного стечения обстоятельств. Мы ни в коем случае не хотим наказывать учеников, преподавателей или администраторов из-за того, что необычайно высокий процент учащихся внесли в свои листы с ответами разумные исправления, сделав это буквально за несколько минут до окончания важного государственного экзамена.

Но словосочетание «необычайно высокий» отнюдь не описывает того, что происходило в Атланте. Количество исправлений неправильных ответов на правильные в листах с ответами некоторых классов превышало норму данного штата на 20–50 среднеквадратических (стандартных) отклонений. (Чтобы было понятнее, что это означает, вспомним, что большинство наблюдений в любом распределении, как правило, отклоняется от среднего значения не более чем на два среднеквадратических отклонения.) Так какова же вероятность того, что учащимся в Атланте удалось по чистой случайности исправить столь большое количество неправильных ответов на правильные? Официальный представитель Министерства образования, который проанализировал эти данные, описал вероятность того, что картина, зафиксированная в Атланте, сложилась исключительно в силу случайного стечения обстоятельств и вовсе не является результатом махинаций, как примерно равную вероятности появления на трибунах стадиона Georgia Dome 70 000 зрителей ростом свыше семи футов. Может такое случиться? Теоретически да, может. Насколько велика вероятность? Чрезвычайно мала!

Тем не менее власти штата Джорджия, столицей которого является Атланта, не смогли предъявить кому-либо обвинение в манипулировании результатами стандартизированных тестов, точно так же как мой преподаватель статистики не мог (и не должен был) вышвырнуть меня из школы только потому, что я сдал выпускной экзамен по статистике успешнее, чем промежуточный. Властям штата Джорджия не удалось доказать факт мошенничества с оценками стандартизированных тестов. Они, конечно, могли отвергнуть нулевую гипотезу, что эти результаты законны, причем «с высокой степенью уверенности» (это означало, что наблюдаемая ими картина была почти невозможной в обычных условиях), и принять альтернативную гипотезу, согласно которой результаты сдачи стандартизованных тестов в Атланте стали следствием махинаций. (В официальных документах они, наверное, использовали более дипломатичную формулировку.) В ходе дальнейшего расследования удалось выявить факты мошенничества с оценками стандартизированных тестов. В объяснительных записках преподавателями приводились факты исправления ими неправильных ответов на правильные, заблаговременного ознакомления учащихся с правильными ответами, предоставления возможности отстающим ученикам списывать правильные ответы у отличников и даже указания учителем правильных ответов в тот момент, когда он останавливался возле парты ученика. Самым вопиющим примером махинаций было исправление ответов преподавателями непосредственно во время пикника, на который они собрались после экзаменов, прихватив с собой экзаменационные работы.

В примере с экзаменами в Атланте мы могли отвергнуть основную гипотезу («махинаций не было»), поскольку картина, зафиксированная в результате сдачи тестов, представлялась крайне маловероятной, если исходить из того, что обмана не было. Но насколько неправдоподобной должна быть нулевая гипотеза, чтобы мы могли ее отклонить и прибегнуть к какому-то альтернативному объяснению?

Одно из самых распространенных пороговых значений, используемых исследователями для отклонения нулевой гипотезы, — 5% (его нередко представляют в форме десятичной дроби: 0,05). Данная вероятность известна как уровень значимости и представляет собой верхнюю границу вероятности возникновения некой картины данных в случае, если бы основная гипотеза оказалась верна. Не спешите выражать свое возмущение: в действительности это не так сложно, как могло показаться на первый взгляд.

Что такое уровень значимости 0,05? Мы можем отвергнуть при нем основную гипотезу, если вероятность исхода, по крайней мере такого же экстремального, как тот, который мы наблюдали бы, если бы она была истинной, оказывалась меньше 5%. Попытаюсь объяснить это положение на простом примере. Хоть я себя и ругаю, но вынужден опять вернуться к нашему пресловутому пропавшему автобусу. Предположим, вам поручено пролить свет на очередную ситуацию, в которую он угодил (честь выполнить эту важную миссию вам оказана, в частности, с учетом героических усилий, приложенных в предыдущей главе). На сей раз вы прикомандированы к группе исследователей Americans’ Changing Lives, которые предоставили вам чрезвычайно ценные данные, призванные помочь в выполнении важной миссии. В каждом из автобусов, арендованных организаторами исследования, находится примерно 60 пассажиров, поэтому мы можем рассматривать их как случайную выборку, сформированную из всей совокупности Americans’ Changing Lives. Итак, вас разбудили рано утром, сообщив о захвате одного из автобусов группой террористов (ярых поборников прав людей, страдающих ожирением) в районе Бостона. Ваша задача — спрыгнуть с вертолета на крышу движущегося автобуса, проникнуть внутрь через аварийный выход и тайком определить, основываясь исключительно на собственных оценках веса пассажиров, являются ли они участниками исследования Americans’ Changing Lives. (Между прочим, этот сюжет ничуть не менее правдоподобен, чем сюжеты большинства приключенческих фильмов, зато гораздо более поучителен с образовательной точки зрения.)

После того как вертолет взлетает с базы войск спецназа, вам вручают автомат, несколько гранат, наручные часы (которые также могут выполнять функции видеокамеры с высоким разрешением) и вычисленные нами в предыдущей главе данные о среднем весе и стандартной ошибке для выборок, сформированных из участников исследования Americans’ Changing Lives. Любая случайная выборка из 60 его участников будет иметь ожидаемый средний вес 162 фунта и среднеквадратическое отклонение 36 фунтов, поскольку именно таковы среднее значение и среднеквадратическое отклонение для всех участников исследования (генеральной совокупности). С помощью этих даных вы можете вычислить стандартную ошибку для среднего значения выборок: s / √n = 36 / √60 = 36 / 7,75 = 4,6. В центре управления миссией представленное ниже распределение выводится на внутреннюю поверхность сетчатки вашего правого глаза, чтобы вы могли использовать его в качестве справочной информации, после того как проникнете в автобус и будете тайно прикидывать вес всех его пассажиров.

Как следует из представленного распределения, можно ожидать, что средний вес приблизительно 95% всех выборок из 60 человек, сформированных из участников исследования Americans’ Changing Lives, будет отстоять от среднего значения совокупности не более чем на две стандартные ошибки, то есть находиться в пределах от 153 фунтов до 171 фунта. И наоборот, лишь в 5 случаях из 100 средний вес выборки из 60 человек, сформированной случайным образом из участников исследования Americans’ Changing Lives, окажется больше 171 фунта или меньше 153 фунтов. (Вы выполняете так называемую двустороннюю проверку гипотезы; разницу между «двусторонней» и «односторонней» проверками я разъясню в , помещенном в конце главы.) Ваш руководитель из центра контртеррористических операций решил, что уровень значимости для вашей миссии равняется 0,05. Если средний вес 60 пассажиров в автобусе, захваченном террористами, окажется больше 171 фунта или меньше 153 фунтов, то вам придется отвергнуть нулевую гипотезу о том, что в автобусе едут участники исследования Americans’ Changing Lives, и принять альтернативную гипотезу, что в автобусе находятся 60 человек, направляюшихся в какой-то другой пункт назначения, и ждать дальнейших указаний.

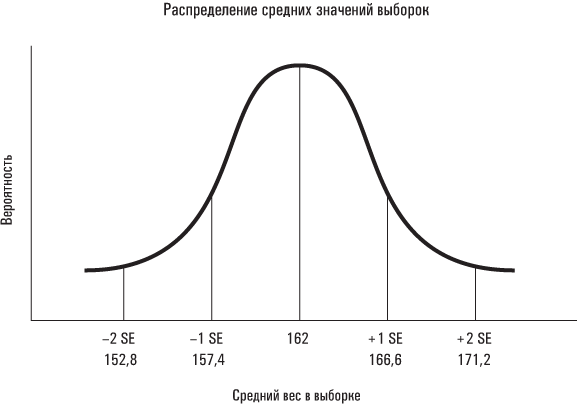
Вы успешно проникаете в движущийся автобус и тайно определяете вес его пассажиров. Оказывается, что он составляет 136 фунтов, то есть меньше среднего значения совокупности более чем на две стандартные ошибки. (Еще одной важной подсказкой для вас становится то, что все пассажиры — дети, одетые в футболки с надписью «Глендейлский хоккейный лагерь».)

Руководствуясь инструкциями по выполнению вашей миссии, вы можете отклонить нулевую гипотезу, что этот автобус перевозит случайную выборку из 60 участников исследования Americans’ Changing Lives. Это означает, что 1) средний вес пассажиров автобуса попадает в диапазон, который, согласно нашим ожиданиям, может наблюдаться лишь в 5 случаях из 100, если бы основная гипотеза была верна и автобус действительно перевозил участников исследования Americans’ Changing Lives; 2) вы можете отвергнуть основную гипотезу с уровнем значимости 0,05 и 3) в среднем в 95 случаях из 100 ваше решение отклонить нулевую гипотезу окажется правильным, а в 5 случаях из 100 вы ошибетесь, то есть придете к заключению, что автобус не перевозил участников исследования Americans’ Changing Lives, хотя на самом деле он их перевозил. Просто случилось так, что средний вес этой выборки участников исследования Americans’ Changing Lives оказался существенно выше или ниже среднего значения для всех участников данного исследования.

Однако на этом ваша миссия не заканчивается. Ваш куратор из центра контртеррористических операций (в киноверсии данного примера эту роль играет Анджелина Джоли) просит вас вычислить p-значение для вашего результата. p-значение — это вероятность получения результата, по меньшей мере такого же экстремального, как тот, который мы наблюдали бы, если бы нулевая гипотеза была верна. Средний вес пассажиров автобуса равняется 136 фунтов, что меньше среднего значения для данной совокупности (участников исследования Americans’ Changing Lives) на 5,7 стандартной ошибки. Вероятность получения результата, по меньшей мере такого же экстремального, если бы это действительно была выборка из участников исследования Americans’ Changing Lives, не превышает 0,0001. (На языке, принятом у исследователей, это было бы обозначено как p < 0,0001.) Завершив свою миссию, вы выпрыгиваете из движущегося автобуса и оказываетесь на пассажирском сиденье автомобиля с откидным верхом, движущегося параллельным автобусу курсом.

[Эта история со счастливым концом. После того как террористы, выступающие за права тучных людей, узнали о том, что в вашем городе проводится Международный фестиваль любителей сосисок, они сразу же согласились отпустить заложников и пообещали продолжать борьбу за права людей, страдающих ожирением, исключительно мирными средствами, пропагандируя и организуя фестивали любителей сосисок по всему миру.]

* * *

Если уровень значимости 0,05 кажется вам в какой-то мере произвольным, то вы абсолютно правы: так оно и есть! Не существует единого стандартизированного статистического порога для отказа от нулевой гипотезы. Значения 0,01 и 0,1 тоже широко используются для выполнения описанного выше анализа.

Очевидно, что отказ от нулевой гипотезы с уровнем значимости 0,01 (то есть когда наши шансы наблюдать какой-либо результат в этом диапазоне, если бы нулевая гипотеза была верна, составляют менее 1 из 100) обладает большим статистическим весом, чем отказ от нулевой гипотезы с уровнем значимости 0,1 (то есть когда наши шансы наблюдать данный результат, если бы нулевая гипотеза была верна, составляют менее 1 из 10). Плюсы и минусы тех или иных уровней значимости будут обсуждаться ниже в этой главе. Пока же запомним следующее: когда мы можем отвергнуть основную гипотезу с некоторым разумным уровнем значимости, соответствующие результаты считаются «статистически значимыми».

В реальной жизни это означает вот что. Когда вы читаете в газете, что те, кто съедает двадцать булочек из отрубей в день, реже страдают раком толстой кишки, чем те, кто не употребляет пищу из отрубей в больших количествах, научные исследования, на основании которых сделан этот вывод, вероятнее всего, выглядели примерно так. 1) Исходя из некоторой объемной совокупности данных ученые определили, что те, кто ежедневно съедает по меньшей мере двадцать булочек из отрубей, болеют раком толстой кишки реже, чем те, кто не увлекается пищей из отрубей. 2) Основная гипотеза исследователей звучала так: поедание булочек из отрубей не влияет на заболеваемость раком толстой кишки. 3) Разницу в заболеваемости раком толстой кишки между теми, кто ест булочки из отрубей, и теми, кто игнорирует их, невозможно объяснить чистой случайностью. Точнее говоря, если поедание булочек из отрубей не связано с заболеваемостью раком толстой кишки, то вероятность чисто случайного наблюдения столь большой разницы должна быть ниже некоторого порога, например 0,05. (Этот порог исследователи должны устанавливать до выполнения статистического анализа, чтобы избежать его выбора постфактум, что бывает очень удобно, когда полученным результатам требуется придать значимость.) 4) Соответствующая научная публикация, наверное, содержит примерно такой вывод: «Мы обнаружили статистически значимую зависимость между ежедневным употреблением двадцати и более булочек из отрубей и снижением заболеваемости раком толстой кишки. Эти результаты значимы на уровне 0,05».

Когда я впоследствии читал об этом исследовании в газете Chicago Sun-Times, по привычке завтракая ветчиной и яйцами, заголовок статьи «20 булочек из отрубей в день уберегут вас от рака толстой кишки!» чрезвычайно меня заинтересовал. Хотя он показался мне гораздо интереснее самой статьи, на мой взгляд, он грешил существенной неточностью. В действительности исследователи вовсе не заявляли, будто поедание булочек из отрубей снижает риск заболевания раком толстой кишки; они лишь продемонстрировали наличие отрицательной корреляции между употреблением булочек из отрубей и заболеваемостью раком толстой кишки в одной объемной совокупности данных. Но такой статистической связи недостаточно, чтобы доказать, что булочки из отрубей послужили причиной «улучшения состояния здоровья». В конце концов, те, кто ест булочки из отрубей (особенно если это целых двадцать штук за день!), наверняка делают много чего другого, чтобы снизить риск заболевания раком толстой кишки, например практически не употребляют красного мяса, регулярно занимаются физическими упражнениями, периодически обследуются и т. п. (Это так называемая систематическая ошибка здорового человека, о которой рассказывалось в главе 7.) В чем же состоит подлинная причина снижения риска заболевания раком толстой кишки: в употреблении булочек из отрубей, каких-то других особенностях поведения или личных качествах, характерных для любителей таких булочек? Это различие между корреляцией и причинно-следственной связью очень важно для правильной интерпретации статистических результатов. Чуть позже мы еще вернемся к утверждению о том, что «корреляция и причинно-следственная зависимость — не одно и то же».

Кроме того, должен отметить, что статистическая значимость ничего не говорит о степени связи. У тех, кто употребляет много булочек из отрубей, заболеваемость раком толстой кишки действительно может оказаться ниже — но насколько ниже? Разница в заболеваемости раком толстой кишки между теми, кто ест много булочек, и теми, кто их не ест, может быть очень несущественной; выяснение статистической значимости лишь означает, что наблюдаемый нами эффект, каким бы ничтожным он ни был, по-видимому, не является чистой случайностью. Допустим, вы узнали, что результаты надлежащим образом организованного и проведенного исследования продемонстрировали наличие статистически значимой положительной связи между поеданием банана перед сдачей школьного экзамена по математике и получением по нему более высокой оценки. Прежде всего вас интересует, насколько силен этот эффект. Если, например, средняя оценка за экзамен по математике составляет 500 баллов, то ее повышение на 0,9 балла вряд ли радикально изменит вашу жизнь. В главе 11 мы еще вернемся к разнице между степенью и значимостью, когда будем говорить об интерпретации статистических результатов.

Однако вывод об «отсутствии статистически значимой связи» между двумя переменными означает, что любую связь между этими переменными можно объяснить исключительно чистой случайностью. Газета The New York Times недавно провела собственное расследование относительно правдивости заявлений некоторых компаний, занимающихся разработкой программного обеспечения, о том, что их продукты повышают успеваемость учащихся. Желание изобличить обман у сотрудников The New York Times возникло после того, как в их руки попали данные, свидетельствующие об обратном. В материале, опубликованном The New York Times, утверждалось, что Университет Карнеги‒Меллон продает компьютерную программу под названием Cognitive Tutor, сопровождаемую лозунгом «Революционный курс математики! Революционные результаты!» Между тем, оценка Cognitive Tutor, проведенная Министерством образования США, показала, что данный продукт «не оказывает никакого заметного влияния на результаты экзаменов по математике в старших классах. (The New York Times считает, что в соответствующей маркетинговой кампании следовало бы использовать более скромные заявления, например: «Заурядный курс математики. Сомнительные результаты».) В действительности анализ десяти программных продуктов, предназначенных для обучения математике или чтению, показал, что девять из них «не оказывают статистически значимого влияния на итоги сдачи экзаменов». Иными словами, любые различия в успеваемости между учащимися, которые пользуются и не пользуются этими программными продуктами, вполне могут быть обусловлены чистой случайностью.

Сейчас я сделаю небольшую паузу, чтобы напомнить вам, почему все это для нас так важно. В мае 2011 года в газете The Wall Street Journal вышла статья под заголовком «Причина аутизма в размере мозга». Это был настоящий прорыв, поскольку причины аутизма до сих пор не установлены. В первом же предложении этой статьи, в которой кратко излагался материал, опубликованный ранее в журнале Archives of General Psychiatry, сообщалось: «У детей, страдающих аутизмом, объем мозга больше, чем у здоровых детей, причем, согласно результатам нового исследования, обнародованным в понедельник, увеличение объема мозга, по-видимому, происходит в возрасте до двух лет». На основе томографического обследования 59 детей, страдающих аутизмом, и 38 здоровых детей ученые из Университета Северной Каролины пришли к выводу, что объем мозга у детей-аутистов на 10% больше, чем у их здоровых сверстников.

Возникает естественный медицинский вопрос: существует ли какая-либо физиологическая особенность у мозга ребенка, страдающего аутизмом? Если да, то это может помочь нам понять причины развития аутизма, а также найти способы его лечения или профилактики.

Появляется и соответствующий статистический вопрос: могут ли исследователи делать далекоидущие выводы относительно общих причин аутизма, основываясь на обследовании сравнительно небольшой группы детей, страдающих аутизмом (59), и еще меньшей контрольной группы (38) — то есть всего 97 участников обследования? Ответ: да, могут. Ученые пришли к заключению, что вероятность наблюдения различий в общем объеме мозга, которые они обнаружили в двух своих выборках, составляла бы 2 из 1000 (p = 0,002), если на самом деле в совокупности в целом не существует никакой разницы в объеме мозга между детьми-аутистами и здоровыми детьми.

Я обратился к оригинальному исследованию, результаты которого были опубликованы в журнале Archives of General Psychiatry. Методы, использованные в нем, ничуть не сложнее уже освоенных нами концепций. Приведу краткий обзор подоплеки этого социально и статистически значимого результата. Во-первых, вы должны признать, что каждая группа детей, 59 из которых страдают аутизмом, а 38 здоровы, представляет собой довольно крупную выборку, сформированную из соответствующих им совокупностей, то есть всех детей-аутистов и всех здоровых детей. Эти выборки достаточно большие для того, чтобы можно было применить центральную предельную теорему. Если вы уже подзабыли, в чем ее суть, я вам напомню: 1) средние значения выборок из какой-либо совокупности будут распределены примерно по нормальному закону вблизи среднего значения соответствующей совокупности; 2) можно ожидать, что среднее значение и среднеквадратическое (стандартное) отклонение выборки будут примерно равняться среднему значению и среднеквадратическому отклонению совокупности, из которой выборка извлечена; и 3) примерно 68% средних значений выборок будут отстоять от среднего значения соответствующей совокупности на расстояние, не превышающее одной стандартной ошибки, примерно 95% — на расстояние, не превышающее двух стандартных ошибок, и т. д.

Проще говоря, любая выборка должна быть очень похожа на совокупность, из которой она сформирована. Несмотря на то что все выборки несколько отличаются друг от друга, среднее значение надлежащим образом сформированной выборки довольно редко будет значительно отклоняться от среднего значения генеральной совокупности. Аналогично, можно ожидать, что две выборки, извлеченные из одной и той же совокупности, будут очень похожи друг на друга. Или, если представить ситуацию несколько иначе: две выборки со средними значениями, сильно разнящимися между собой, с наибольшей вероятностью сформированы из разных совокупностей.

Вот краткий пример, который должен быть понятен на интуитивном уровне. Допустим, ваша нулевая (основная) гипотеза гласит, что средний рост профессиональных баскетболистов равен среднему росту остальной части взрослого мужского населения. Вы формируете произвольным образом выборку из 50 профессиональных баскетболистов и выборку из 50 взрослых мужчин-неспортсменов. Допустим, что средний рост членов первой группы (баскетболисты) составляет 6 футов и 7 дюймов, а второй (небаскетболисты) — 5 футов и 10 дюймов (разница — 9 дюймов). Какова вероятность зафиксировать столь большую разницу между значениями среднего роста у этих двух выборок, если бы действительно (как мы предположили) средний рост профессиональных баскетболистов и всего остального взрослого мужского населения страны не отличался? «Нетехнический» ответ: чрезвычайно низкая.

Базовая методология, использовавшаяся при выполнении исследования аутизма, точно такая же. В упомянутой нами статье сравниваются несколько показателей объема мозга у разных выборок детей. (Измерения выполнялись по методу визуализации с помощью магнитного резонанса у детей в возрасте двух, четырех и пяти лет.) Я сосредоточусь лишь на одном показателе: общем объеме мозга. Нулевая гипотеза исследователей, скорее всего, заключалась в том, что анатомические различия в головном мозге детей-аутистов и здоровых детей отсутствуют. Альтернативная гипотеза — что головной мозг детей-аутистов существенно отличается от головного мозга здоровых детей. Вывод, к которому пришли ученые, по-прежнему оставляет много вопросов, однако указывает, в каком направлении должны проводиться дальнейшие эксперименты.

В рассматриваемом нами исследовании средний объем головного мозга детей, страдающих аутизмом, составляет 1310,4 кубических сантиметра; средний объем головного мозга детей в контрольной группе равен 1238,8 кубических сантиметра. Таким образом, разница в среднем объеме головного мозга у этих двух групп составит 71,6 кубических сантиметра. Какова вероятность наблюдения такого результата, если бы на самом деле разницы в среднем объеме головного мозга у детей-аутистов и здоровых детей во всей совокупности не было?

Из материала предыдущей главы вы, возможно, помните, как вычислить стандартную ошибку для каждой выборки: s / √n, где s — среднеквадратическое отклонение данной выборки, а n — количество наблюдений. Соответствующие величины приведены в рассматриваемой нами статье. Стандартная ошибка для общего объема головного мозга 59 детей в выборке детей-аутистов составляет 13 кубических сантиметров, а 38 детей в контрольной группе — 18 кубических сантиметров. Согласно центральной предельной теореме, для 95 выборок из 100 среднее значение выборок будет отстоять от истинного среднего значения совокупности на расстояние, не превышающее двух стандартных ошибок (в ту или другую сторону).

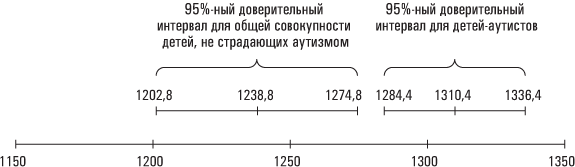
Таким образом, на основании нашей выборки можно заключить, что в 95 случаях из 100 интервал 1310,4 кубических сантиметра ±26 (что равняется двум стандартным ошибкам) будет содержать средний объем головного мозга для всех детей, страдающих аутизмом. Это выражение называется доверительным интервалом. Мы можем с 95%-ной уверенностью утверждать, что диапазон от 1284,4 до 1336,4 кубических сантиметра содержит средний общий объем головного мозга для детей-аутистов в их общей совокупности.

Используя ту же методологию, мы можем с 95%-ной уверенностью утверждать, что интервал 1238,8 ± 36, или диапазон от 1202,8 до 1274,8 кубических сантиметра, будет включать средний объем головного мозга для здоровых детей в генеральной совокупности.

Да, вас, наверное, утомило обилие числовых показателей. Возможно, вы уже зашвырнули книгу в дальний угол. Если же еще нет (или раскаялись и возобновили чтение), то должны были обратить внимание на то, что наши доверительные интервалы не перекрываются. Нижняя граница 95%-ного доверительного интервала для среднего объема головного мозга детей-аутистов в общей совокупности (1284,4 кубических сантиметра) все же выше, чем верхняя граница 95%-ного доверительного интервала для среднего объема головного мозга здоровых детей в общей совокупности (1274,8 кубических сантиметра), что иллюстрируется приведенной ниже диаграммой.

Это первый намек на вероятность существования какой-то анатомической особенности в головном мозге детей, страдающих аутизмом. Однако это всего лишь подсказка. Ведь сделанные заключения основываются на данных, описывающих небольшое число детей (менее 100 человек). Нельзя исключать вариант, что мы имеем дело с какими-то аномальными выборками.

Одна финальная статистическая процедура способна внести ясность в ситуацию. Если бы статистика была одним из олимпийских видов спорта, например фигурным катанием, то это было бы последним видом программы выступлений, после которой преданные болельщики бросают на лед букеты цветов. Мы можем точно вычислить вероятность наблюдения по меньшей мере столь же значительной разницы средних значений (1310,4 кубических сантиметра в сравнении с 1238,8 кубическими сантиметрами), если действительно между объемом головного мозга детей-аутистов и всех остальных детей в общей совокупности никакого отличия нет. Мы можем найти p-значение для наблюдаемой разницы в средних значениях.

Чтобы вы прямо сейчас не зашвырнули эту книгу в самый дальний угол комнаты, соответствующая формула будет приведена в приложении. Впрочем, на интуитивном уровне все должно быть достаточно понятно. Если мы извлекаем две большие выборки из одной и той же совокупности, то можно ожидать, что их средние значения будут очень близки между собой. Более того, в идеале они должны быть одинаковы. Если бы, например, средний рост выбранных мною 100 баскетболистов из НБА составлял 6 футов и 7 дюймов, то я был бы вправе ожидать, что в какой-нибудь другой случайной выборке 100 баскетболистов из НБА средний рост игроков будет близок к 6 футам и 7 дюймам. Ладно, возможно, средний рост игроков в этих двух выборках будет отличаться на один-два дюйма. Однако вероятность того, что он будет разниться на 4 дюйма, окажется низкой, а того, что на 6 или 8 дюймов, будет еще ниже. Мы можем вычислить стандартную ошибку для разности между средними значениями двух выборок, которая может служить мерой ожидаемого разброса (но в среднем) при вычитании среднего значения одной выборки из среднего значения другой. (Как указывалось ранее, соответствующая формула приводится в  к этой главе.) Важно то, что мы можем использовать эту стандартную ошибку для определения вероятности того, что две выборки сформированы из одной и той же совокупности. Принцип действия этого механизма таков.

1. Если две выборки сформированы из одной и той же совокупности, мы имеем все основания предполагать, что разница между их средними значениями равна нулю.
2. Согласно центральной предельной теореме, в повторных выборках разница между этими двумя средними значениями будет распределена примерно по нормальному закону. (Итак, вы уже влюбились в центральную предельную теорему или еще нет?)
3. Если обе выборки действительно сформированы из одной и той же совокупности, то приблизительно в 68 случаях из 100 разница между их средними значениями будет отличаться от нуля не более чем на одну стандартную ошибку, в 95 случаях из 100 — не более чем на две стандартные ошибки, а примерно в 99,7 случая из 100 — не более чем на три стандартные ошибки. Так вот что побудило исследователей сделать вывод, о котором мы узнали из статьи об аутизме, опубликованной в The Wall Street Journal.

Как указывалось ранее, разница в среднем объеме головного мозга между выборкой детей-аутистов и контрольной группой составляет 71,6 кубичес­ких сантиметра. Стандартная ошибка для этой разницы — 22,7. Это означает, что разница между средними значениями двух выборок больше нуля на три стандартные ошибки. Можно ожидать, что столь (или еще более) экстремальный исход окажется возможным лишь в 2 случаях из 1000, если эти выборки сформированы из одной и той же совокупности.

Как отмечалось выше, авторы статьи, опубликованной в Archives of General Psychiatry, сообщают о p-значении, равном 0,002. Теперь вы понимаете, откуда взялась эта величина.

Несмотря на все достоинства статистического вывода, он не лишен недостатков. И они становятся очевидны из примера, приведенного в начале главы. Если вы помните, в нем речь шла о моем преподавателе статистики, заподозрившем меня в обмане. Процесс статистического вывода основывается на понятии вероятности, а вовсе не на абсолютной и не вызывающей ни малейшего сомнения достоверности. Таким образом, когда речь идет о проверке той или иной гипотезы, мы имеем дело с фундаментальной дилеммой.

Эта статистическая реальность заявила о себе во весь голос в 2011 году, когда Journal of Personality and Social Psychology готовился опубликовать одну научную статью, которая на первый взгляд ничем особенным не выделялась. Некий профессор Корнелльского университета предложил нулевую гипотезу, а затем, на основе полученных им экспериментальных результатов, отверг ее с уровнем значимости 0,05. Этот результат произвел настоящий фурор в научных кругах, а также широко освещался в ведущих средствах массовой информации, таких как The New York Times.

Достаточно сказать, что статьи в Journal of Personality and Social Psychology обычно не привлекают к себе внимания СМИ. Что же вызвало на сей раз столь повышенный интерес прессы? Упомянутый мной исследователь проверял способность человека к экстрасенсорному восприятию (Extra Sensory Perception — ESP). Основная гипотеза ученого отрицала существование ESP; альтернативная подтверждала. Чтобы изучить вопрос, исследователь предложил большой выборке людей, которых он пригласил поучаствовать в эксперименте, рассмотреть два «занавеса», представленных на экране монитора. Компьютерная программа случайным образом помещала некое эротическое изображение то за одним, то за другим «занавесом». В ходе повторяющихся попыток испытуемым удалось правильно выбрать «занавес», за которым скрывалось эротическое изображение, в 53 случаях из 100, тогда как, согласно теории вероятностей, это должно происходить лишь в 50 случаях из 100. Достаточно большой размер выборки позволил ученому отклонить нулевую гипотезу и принять альтернативную. Решение опубликовать статью об этом эксперименте подверглось широкой критике на том основании, что какое-то одно статистически значимое событие вполне может оказаться следствием чистой случайности, особенно при отсутствии каких-либо других свидетельств, подтверждающих или даже объясняющих полученный результат. Статья в The New York Times так резюмировала критические высказывания: «Утверждения, которые бросают вызов практически всем законам науки, по определению являются экстраординарными и, как правило, требуют экстраординарных, неопровержимых доказательств. Нежелание учитывать это обстоятельство — как того требует общепринятый научный метод — делает результаты многих исследований гораздо значимее, чем они есть на самом деле».

Одним из достойных ответов на подобную критику был бы выбор более жесткого порога для определения статистической значимости, например 0,001. Однако это порождает собственные проблемы. Выбор надлежащего уровня значимости в любом случае предполагает определенный компромисс.

Если наше «бремя доказательства», которое позволило бы отвергнуть основную гипотезу, будет чересчур низким (например 0,1), то нам придется периодически отклонять нулевую гипотезу, хотя на самом деле она верна (я подозреваю, что именно так и произошло при исследовании ESP). На языке статистики это называется ошибкой первого рода. Рассмотрим пример из судебной практики в США, где нулевая гипотеза заключается в том, что подсудимый (ответчик) невиновен, а порогом, когда она отвергается, является «критерий доказанности при отсутствии обоснованного сомнения» (то есть подсудимый признается виновным при отсутствии обоснованного сомнения в его невиновности). Допустим, мы решили ослабить этот порог, обозначив его, например, как «сильное подозрение, что подсудимый все же совершил данное преступление». Это должно гарантировать, что за решеткой окажется большее число настоящих преступников — а вместе с ними и большее число ни в чем не повинных людей. В статистическом контексте это эквивалентно использованию относительно низкого уровня значимости (например 0,1).

Ладно, «в 1 случае из 10» — не такое уж маловероятное событие. Рассмотрим эту проблему в контексте утверждения нового лекарства от рака. На каждые десять препаратов, которые мы одобряем с этим относительно низким «бременем статистического доказательства», один на практике оказывается неэффективным, а в процессе тестирования показывает обнадеживающие результаты лишь по чистой случайности. (Или, если воспользоваться примером из судебной практики, из каждых десяти подсудимых, признанных виновными, один фактически невиновен.) Ошибка первого рода заключается в ошибочном отказе от основной гипотезы. Иногда это называют «ложным позитивом», хотя употребление такого термина кажется несколько парадоксальным. Вот один способ примириться с подобным жаргоном. Когда вы приходите к врачу, чтобы выяснить, не страдаете ли вы некой болезнью, основная гипотеза заключается в том, что вы ею не страдаете. Если результаты анализов позволяют отвергнуть нулевую гипотезу, то врач говорит, что у вас положительный результат анализов. А если у вас положительный результат анализов, хотя в действительности вы не больны, то это и есть случай «ложного позитива».

Как бы то ни было, чем ниже «статистическое бремя» для отклонения нулевой гипотезы, тем выше вероятность «ложного позитива». Очевидно, что мы предпочли бы не утверждать неэффективные лекарства от рака и не отправлять невинных людей за решетку.

Но здесь есть один нюанс. Чем выше порог для отказа от нулевой гипотезы, тем вероятнее, что нам не удастся отвергнуть ту нулевую гипотезу, которую на самом деле следовало было бы отвергнуть. Если бы нам потребовалось не менее пяти свидетелей, чтобы признать виновным каждого обвиняемого, то на свободе оказалось бы немалое число настоящих преступников. (Разумеется, при этом за решетку не угодили бы многие невиновные люди.) Если при клинических испытаниях всех новых лекарств от рака мы примем уровень значимости 0,001, то мы действительно минимизируем утверждение неэффективных препаратов. (В этом случае будет лишь 1 шанс из 1000 ошибочно отвергнуть нулевую гипотезу, которая заключается в том, что испытываемое лекарство эффективно не более чем плацебо.) Однако при этом возникает риск не допустить на рынок много эффективных лекарств, поскольку мы установили очень высокую планку для их утверждения. На языке статистики это называется ошибкой второго рода, или «ложным негативом».

Какая же из двух ошибок хуже? Это зависит от конкретных обстоятельств. Самое важное — что вы признаете необходимость компромисса. В статистике «бесплатный завтрак» невозможен. Рассмотрим перечисленные ниже нестатистические ситуации, каждая из которых предполагает достижение определенного компромисса между ошибками первого и второго рода.

1. Спам-фильтры. Основная гипотеза: любое конкретное сообщение, приходящее по электронной почте, не спам. Ваш спам-фильтр отыскивает признаки, которые могут использоваться для отказа от нулевой гипотезы для того или иного конкретного сообщения, например огромные списки рассылки или наличие фраз типа «удлинение пениса». Ошибка первого рода предполагает отбраковку сообщения, которое на самом деле не является спамом («ложный позитив»). Ошибка второго рода предполагает пропуск спама через фильтр и его попадание в ваш почтовый ящик («ложный негатив»). Сравнивая последствия от потери важного сообщения и незначительное раздражение, вызванное получением совершенно не интересующего вас письма, содержащего, скажем, рекламу БАДов, большинство людей, скорее всего, предпочтут терпеть неудобства, обусловленные ошибками второго рода. Оптимально разработанный спам-фильтр должен требовать относительно высокой степени определенности, прежде чем отвергнуть нулевую гипотезу и заблокировать соответствующее сообщение.
2. Проверка на наличие раковых заболеваний. Существуют многочисленные тесты для раннего выявления раковых заболеваний, например маммография (рак молочной железы), ПСА-тест (рак простаты) и даже магнитно-резонансная визуализация (МРТ) всего тела для выявления всего, что может вызывать подозрения. Основная гипотеза для каждого, кто проходит такое обследование, заключается в том, что он не болен раком. Проверка на наличие раковых заболеваний используется для того, чтобы отвергнуть нулевую гипотезу, если результаты тестирования вызывают подозрения. Соответствующее предположение всегда исходит из того, что ошибка первого рода («ложный позитив», что в конечном счете означает отсутствие заболевания) безусловно предпочтительнее ошибки второго рода («ложный негатив», который означает, что диагностирование не выявило заболевания, которое на самом деле имеется). Проверка на наличие раковых заболеваний является полной противоположностью примеру со спам-фильтром. Врачи и пациенты готовы мириться с умеренным количеством ошибок первого рода («ложный позитив»), чтобы избежать вероятности появления ошибок второго рода («ложный негатив»), когда пациенту не диагностируется раковое заболевание, хотя в действительности он болен. Впрочем, в последнее время специалисты в области политики охраны здоровья подвергают сомнению такой подход из-за высоких издержек и побочных эффектов, связанных с «ложными позитивами».
3. Поимка террористов. В этой ситуации неприемлема ни ошибка первого, ни ошибка второго рода. Именно поэтому в обществе продолжаются дебаты, связанные с поиском подходящего баланса между борьбой с терроризмом и защитой гражданских прав. Основная гипотеза в данном случае заключается в том, что человек не террорист. Как и в обычном уголовном контексте, нам не хотелось бы совершать ошибки первого рода и отправлять невиновных в тюрьму Гуантанамо. Однако в мире, где накоплено большое количество оружия массового поражения, даже одного террориста опасно оставлять на свободе (ошибка второго рода), поскольку это может повлечь за собой поистине катастрофические последствия. Именно поэтому — нравится вам это или нет — власти Соединенных Штатов удерживают в Гуантанамо людей, подозреваемых в терроризме, основываясь при этом даже на меньшей доказательной базе, чем могло бы потребоваться для вынесения им обвинительного приговора в обычном уголовном суде.

Статистический вывод — это не волшебная палочка и отнюдь не безошибочный метод. Тем не менее это замечательный инструмент для осмысления мира. Мы можем глубже понять многие явления нашей жизни лишь путем нахождения им наиболее вероятного объяснения. Многие из нас делают это постоянно (например, мы говорим: «Мне кажется, этот молодой человек, развалившийся на полу в окружении множества пустых банок из-под пива, хватил лишку», а не «Мне кажется, что этого молодого человека, развалившегося на полу в окружении множества пустых банок из-под пива, отравили террористы»).

Статистический вывод лишь формализует процесс.

Отправить

Рауан

Хорошая книга