«Изящные» условные абстракции

РИЧАРД НИСБЕТТ

Социопсихолог, соуправляющий программы «Культура и познание», Мичиганский университет, автор книги Intelligence and How to Get It: Why Schools and Cultures Count («Ум и как его получить: почему школа и культура имеют значение»)

1. Университету необходимо привести в порядок старую больницу. Как показали расчеты, ремонт старого здания будет стоить столько же, что и строительство нового. Главный аргумент сторонников ремонта сводится к тому, что строительство здания обойдется очень дорого, сносить его – настоящая расточительность. Главный аргумент тех, кто склоняется к строительству нового здания, заключается в том, что оно будет, несомненно, более современным, чем старое. Как вы считаете, что разумнее – отремонтировать старую больницу или построить новую?

2. Дэвид Л. заканчивает учебу в школе и выбирает, в какой колледж поступить. У него два варианта, одинаковых с точки зрения престижа, стоимости обучения и удаленности от дома. У Дэвида есть друзья в обоих колледжах. Друзьям из колледжа А нравятся и преподавание, и атмосфера. Те, кто учится в колледже Б, недовольны ни тем, ни другим. Дэвид посетил оба колледжа, но его впечатления сильно отличаются от впечатлений друзей. В колледже А он общался с несколькими студентами, но они не показались ему особо интересными или дружелюбными, а профессора, с которыми он хотел поговорить, отмахнулись от него. В колледже Б он встретил несколько умных и дружелюбных студентов и два профессора проявили к нему явный интерес. Как вы думаете, в какой колледж надо поступать Дэвиду?

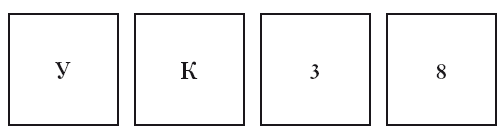
3. Какие из следующих карт нужно перевернуть, чтобы определить, насколько истинно следующее правило: если на одной стороне карты гласная буква, то на другой – нечетное число?

Некоторые соображения:

Вопрос 1. Если вы считаете, что университету следует ремонтировать старое здание, потому что на его постройку уже было потрачено много средств, вы попали в ловушку «необратимых затрат». Деньги, потраченные когда-то на строительство больницы, сегодня не имеют значения – здание рушится, его бывшая стоимость не должна влиять на ваше решение. Амос Тверски и Даниэль Канеман отмечали, что избежать подобных ловушек помогут простые мысленные эксперименты. Например, такой: представьте, что у вас два билета на игру национальной сборной и стадион находится в шестидесяти километрах от вашего дома. Но пошел снег, и вы узнали, что ваш любимый игрок получил травму и не выйдет на поле. Пойти ли вам на игру, или выбросить деньги на ветер и пропустить матч?

Чтобы ответить на этот вопрос, задайте себе еще один. Допустим, у вас нет билетов, а вам позвонил друг и сказал, что у него есть два билета, которые ему не нужны, и предложил их вам. Вы возьмете? Если вы ответите: «Ты что, шутишь? На дворе снег, и главный игрок не играет», – тогда идти на стадион не стоит. Неважно, что вы выложили за билеты кругленькую сумму, – их стоимость в любом случае снизилась, и вы не сможете их окупить просто тем, что сделаете что-то против своего желания.

Нельзя попадаться в ловушку необратимых затрат – это азбука для экономистов, но я обнаружил, что тот единственный курс экономики, который есть в колледжах, совсем не разъясняет студентам, что это такое. Как оказалось, истории вроде билетов на баскетбол очень помогают.

Вопрос 2. Если вы считаете, что Дэвид – не то же самое, что его друзья, что ему следует идти туда, где ему понравилось, значит, вы пренебрегаете законом больших чисел (ЗБЧ). Дэвид провел в каждом колледже по одному дню, а его друзья – сотни дней. Если Дэвид не считает, что у его друзей причудливые вкусы, ему следует проигнорировать собственные впечатления и пойти в колледж А.

После прохождения одного курса статистики в колледже понимание закона больших чисел улучшится. А после нескольких курсов вы наверняка будете использовать ЗБЧ постоянно.

Вопрос 3. Правильный ответ: карты «У» и «8». Если вы ответили иначе, то присоединились к 90 % студентов Оксфорда (согласно исследованию психологов Питера Уэйсона и Филиппа Джонсона-Лэрда). К сожалению, вы – и они – ошибаетесь, потому что не учитываете условную абстракцию условного высказывания. Чтобы проверить условие «если Р, то Q», нужно показать, что Р связано с Q, а не-Q с Р не связано. Курс логики не учит людей отвечать на такие вопросы. Даже степень доктора философских наук не означает, что вы умеете применять логику условных высказываний для решения простых проблем вроде вопроса № 3 или насущных вопросов, с которыми мы сталкиваемся в повседневной жизни.

Некоторые условные абстракции «изящны», потому что их легко добавить в набор своих когнитивных инструментов. Другие «неуклюжи» и не так хорошо подходят. Чтобы улучшить способность учеников думать, педагоги должны понимать, какие абстракции изящны и легко усваиваются, а каким тяжело научить. Преподаватели веками опирались на предположение, что формальная логика улучшает мыслительный процесс – то есть делает людей умнее в повседневной жизни. Возможно, это предположение ошибочно (как сказал Бертран Рассел – и, наверное, он прав, – «силлогизмы, которые изучали монахи в средневековой Европе, были так же бесплодны, как и сами монахи»). Но многие важные условные абстракции, включая те, что предлагали некоторые авторы на Edge.org, уже вошли в практику преподавания. Немногие задачи достойны того же внимания, что и поиск наилучших способов преподавания условных абстракций.