Книга: Теория ограничений Голдратта Системный подход к непрерывному совершенствованию
Назад: Как работать с этой главой
Дальше: Примечание: сложные зависимости
Описание критериев проверки логических построений
Я знаю: вам кажется, будто вы понимаете, о чем, по вашему мнению, я говорю. Но не уверен, осознаете ли вы, что слышите совсем не то, что я хотел бы до вас донести.
Неизвестный источник
Ясность
Ясность — первый параметр, который нужно учитывать, анализируя причинно-следственные связи. Строго говоря, ясность — категория не логическая, а коммуникативная.
Почему ясность на первом месте
Фактор ясности проверяется первым, чтобы до начала анализа собственно логики устранить все недопонимания, связанные с нечеткой или неполной передачей информации. Любой конфликт всегда так или иначе связан со сбоями в процессе коммуникации. Соблюдение принципа ясности сглаживает потенциально возможный конфликт между слушающим и говорящим и позволяет поддерживать общение на профессиональном, а не на межличностном уровне.
Принцип первоочередной проверки ясности высказываний приводит нас к своего рода правилу применения КПЛП, которое в формулировке Стивена Р. Кови из книги «Семь навыков высокоэффективных людей» (The Seven Habits of Highly Effective People[13]) гласит:
Не старайтесь быть понятыми, постарайтесь сначала сами понять других.
Придерживаясь этого правила, мы не потеряем логики построений из-за неумения общаться друг с другом.
Что такое ясность
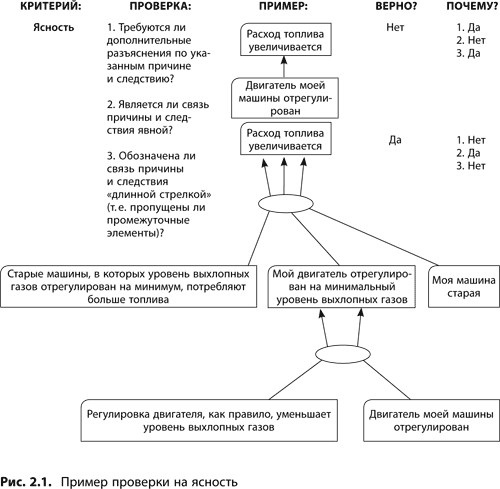
Если слушающий понимает говорящего, то принцип ясности не нарушен. Проверка на ясность — первый шаг в анализе логики, прежде всего нужно убедиться, что все одинаково и верно понимают исходное утверждение выступающего. Таким образом, речь идет не о том, согласна ли аудитория с говорящим, а о том, понимают ли слушающие вообще, что хочет сказать докладчик. Только когда есть уверенность в том, что взаимопонимание достигнуто, можно переходить к оценке логичности высказанного. Ниже приведены некоторые примеры сбоев при передаче информации:
слушающий не понимает смысла высказываний говорящего;
слушающий не понимает, в чем важность высказываний говорящего;
слушающий не понимает значения отдельных слов, фраз или использования слов в данном контексте;
слушающий не видит связи между приведенными причинами и следствиями;
слушающий не видит некоторых промежуточных элементов, которые подразумеваются, но явно говорящим не обозначены (в диаграммах причин и следствий это часто называется «длинная стрелка»).
До сих пор мы говорили о критерии ясности на примере общения людей, однако основное внимание в этой главе уделено использованию критерия ясности при создании, анализе и корректировке логических деревьев.
Говоря о логических деревьях, мы будем употреблять слово «утверждение» для обозначения высказываний выступающих (письменных или устных). Понятие «утверждение» будет детально описано в следующем разделе.
На рис. 2.1 дается пример и вопросы для проверки логических построений на ясность. Рисунок 8.4 «Построение диалога при помощи КПЛП» в конце главы 8 подробно разъясняет, как выявлять случаи несоблюдения принципа ясности, а также реагировать на критику при анализе диаграмм.
Главная трагедия науки в том, что прекрасные гипотезы часто разрушаются неприглядными фактами.
Томас Хаксли
Наличие утверждения
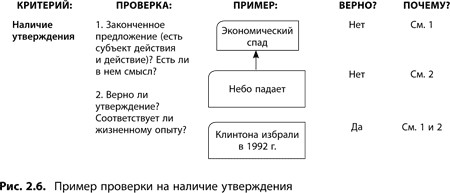
При проведении логического анализа под утверждением мы будем понимать высказывание, содержащее законченную мысль. В широком смысле утверждение может подразумевать высказывание в разговоре, дискуссии, лекции или письменном тексте, но чаще всего мы будем использовать это понятие для обозначения причины или следствия в логических деревьях. Наличие утверждения ставится под вопрос (т.е. логичность некоего построения оспаривается по этому критерию), если по отношению к высказыванию верно хотя бы одно из следующих замечаний:
высказывание не является законченной мыслью (обычно это означает, что предложение построено с нарушением грамматических правил);
высказывание выстроено логически неправильно (т.е. в одном предложении высказаны несколько мыслей или между частями присутствуют скрытые причинно-следственные отношения «если — то»);
с первого взгляда утверждение кажется неверным.
Законченность
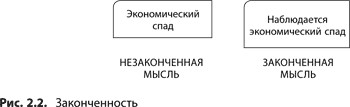
Как правило, законченная мысль выражается грамматически правильным простым предложением. Использование законченных предложений обязательно для построения логических деревьев. В предложении должны присутствовать как минимум субъект действия и действие, а часто имеется и объект, на который действие направлено. Недопустимо употребление неличных местоимений (таких, как «это», «этот», «тот») — см. рис. 2.2.
Например, фраза «экономический спад» сама по себе не является законченной мыслью, так как возникает вопрос: а что же именно сообщается про этот экономический спад? Если к началу рассматриваемого высказывания нельзя добавить слова «если» или «то», его нельзя использовать в логическом дереве. Таким образом, с точки зрения законченности для логического дерева подойдет формулировка «наблюдается экономический спад».
Структура
Существует формальный способ проверки утверждения — это проверка на соблюдение структурных норм построения высказывания. Следование этим правилам необходимо для избежания путаницы, простоты и наглядности и создания логически «сухих», однозначных схем. Таких норм две.
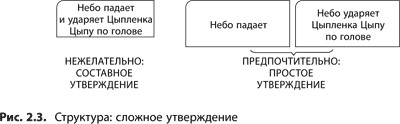
Использовать простые предложения (см. рис. 2.3) — одно отдельное утверждение не должно содержать в себе более одной мысли. Например, утверждение «Небо падает» несет в себе одну мысль. Предложение «Небо падает и ударяет Цыпленка Цыпу[14] по голове» будет уже составным утверждением: в нем выражены две мысли, и каждая может служить отдельным утверждением.
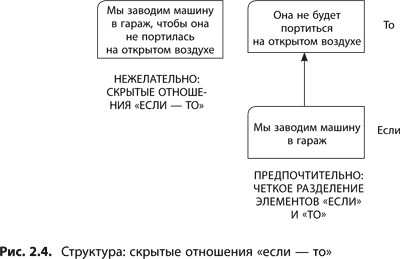
Исключать скрытые причинно-следственные отношения (см. рис. 2.4). Сложно отделить причины от следствий, если они высказаны в одном утверждении. Может показаться, что избежать этой ошибки легко: просто не использовать в утверждении слов «если» и «то». Но причинно-следственные отношения могут выражаться скрыто, и тогда признаком их наличия служат союзы «для того чтобы» и «потому что». Итак, даже если слов «если — то» не видно, это вовсе не означает, что все в порядке.
Рассмотрим два примера. Утверждение гласит: «Мы заводим машину в гараж, чтобы она не портилась на открытом воздухе» — и здесь нет никаких «если — то». Но мы видим «чтобы» и понимаем, что фразу можно сформулировать и иначе: «Если мы заводим машину в гараж, то она не будет портиться на открытом воздухе». Налицо скрытое утверждение «если — то». Так же и предложение с «потому что» может оказаться переформулированным утверждением с «если — то». Например, утверждение «Он оскорбляет меня, потому что я ему не нравлюсь» можно выразить и как «Если я ему не нравлюсь, то он меня оскорбляет».
Примечание: обычно чем проще вы формулируете свою мысль (утверждение) при построении логических деревьев, тем лучше.
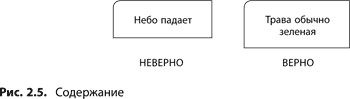
Содержание
После того как утверждение прошло проверку на ясность, законченность и на соблюдение структурных норм, проверяется его содержание (т.е. верно оно или нет — см. рис. 2.5). В нашем случае утверждение верно, если является здравым и основано на фактах. Оно должно соответствовать опыту аудитории или же представлять собой заключение, с которым слушающий может легко согласиться.
Например, утверждение «Небо падает» обычно не соответствует опыту большинства из нас. Поэтому даже хотя оно и соответствует критериям ясности, законченности и структурным нормам, это высказывание вряд ли можно назвать утверждением, подходящим для использования в логическом дереве. А вот фраза «Трава обычно зеленая» — это законченное, структурно правильное и верное высказывание, соответствующее критерию наличия утверждения. Итак, утверждение может считаться логичным (т.е. критерий наличия утверждения признается соблюденным), если это законченная, выстроенная по структурным нормам и содержательная мысль.
Примечание: проверка содержания применима только к утверждениям, описывающим предпосылки/условия возникновения некоторых событий, а не сами события в развитии. Например, описанием предпосылок/условий будет фраза «В полдень солнце находится в зените». Пример события в динамике: «Я веду машину». При работе с деревьями будущей реальности и перехода можно оценивать законченность или структуру утверждений, описывающих события в динамике, но нельзя оценить, верно такое утверждение или нет, так как этих событий и их последствий еще не существует.
На рис. 2.6 дается пример и вопросы для проверки на наличие утверждения. Рисунок 8.4 «Построение диалога при помощи КПЛП» в конце главы 8 подробно разъясняет, как выявлять случаи несоблюдения принципа наличия утверждения, а также реагировать на критику при анализе логических деревьев.
Бойтесь полуправды. Ведь у вас может оказаться не та половина.
Неизвестный источник
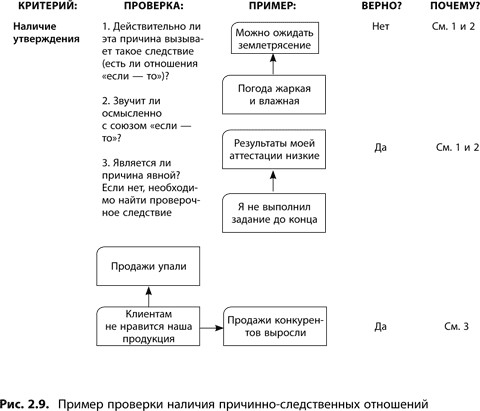
Наличие причинно-следственных отношений
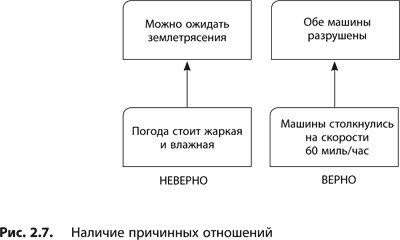
Логическое построение может быть оспорено по этому критерию, если у аудитории возникают сомнения в том, что приведенная причина действительно вызывает указанные следствия. Если критерий наличия утверждения нужен для оценки правильности построения утверждений как таковых, то наличие причинно-следственных отношений исследуется для проверки правильности связей (стрелок) между утверждениями. При этом задаются следующие вопросы.
Действительно ли данная причина вызывает это следствие? Правда ли существуют отношения «если — то»? Часто помогает развеять сомнения «озвучивание» стрелки в следующей формулировке: «Если причина такая, то мы должны прийти к такому следствию». При проговаривании с использованием конструкции «если — то» причинно-следственные связи должны звучать правдоподобно (см. рис. 2.7).
Внимание: При анализе нужно быть внимательным и читать/слышать не то, что кажется, а только то, что действительно написано/сказано. Избежать этой проблемы позволяет проверка по критерию ясности.
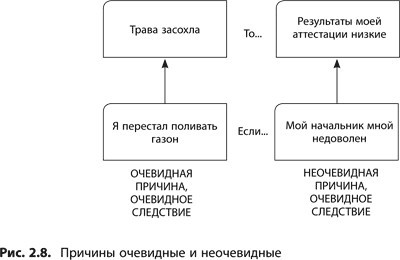
Является ли причина явной? «Явная» причина — значит измеримая, видимая. Зачастую следствие легко обнаружить и измерить, а причину нет (см. рис. 2.8). Например, факт, содержащийся в утверждении «Мой начальник мной недоволен», сам по себе нельзя по-настоящему зафиксировать и оценить (если только начальник сам об этом не сказал). Второй пример на этом рисунке — очевидная, видимая причина: «Я перестал поливать газон». И в том и в другом примере следствие измеримо и видимо, но в первом случае приводится неочевидная причина. Чтобы подтвердить верность установленных причинно-следственных отношений в подобной ситуации, необходимо найти еще хотя бы одно следствие той же причины, которое можно наблюдать непосредственно. Этот прием более подробно будет описан далее, когда речь пойдет о критерии существования проверочного следствия.
На рис. 2.9 дается пример и вопросы для проверки наличия причинно-следственных отношений. Рисунок 8.4 «Построение диалога при помощи КПЛП» в конце главы 8 подробно разъясняет, как выявлять случаи несоблюдения принципа наличия причинно-следственных отношений, а также реагировать на критику при анализе диаграмм.
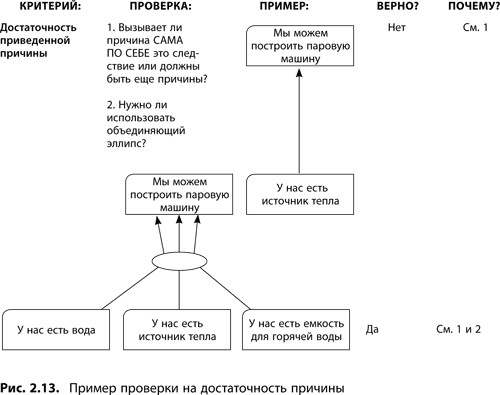
Достаточность приведенной причины
Поскольку наш мир — это переплетение сложных систем, достаточность приведенной причины — самый трудный вопрос в работе с логическими деревьями и просто в общении людей. Когда речь идет о сложных, многогранных взаимосвязях, немногие явления имеют только одну-единственную причину. В большинстве случаев конкретное следствие будет вызвано либо рядом взаимосвязанных факторов, либо несколькими независимыми причинами. В этом разделе мы увидим, как ряд взаимозависимых факторов может служить достаточной причиной некоего следствия, а также научимся распознавать недостаточность приведенных аргументов. Наличие альтернативной причины обсудим в следующем разделе.
Можно говорить о нарушении принципа достаточности причины, если возникают сомнения в том, что заявленная причина сама по себе способна вызывать описанное событие. Как и критерий наличия причинно-следственных отношений, принцип достаточности приведенной причины нацелен на связь (стрелку) между утверждениями, а не на само утверждение. Высказывая сомнения в достаточности причины, мы на самом деле говорим: «Я согласен, что заявленная причина действительно имеет место, но ведь ее одной недостаточно, чтобы вызвать данное следствие. Должен существовать еще какой-то фактор, который не был упомянут».
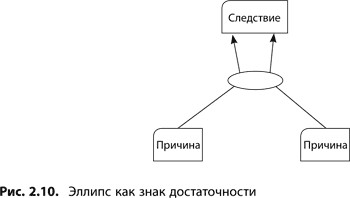
Эллипс
Как в логическом дереве можно показать, что для существования некоторого события необходима совокупность нескольких причин? Для отображения этого явления причины соединяются со следствием стрелками, проходящими через объединяющий эллипс (см. рис. 2.10), который иногда из-за формы еще называют линзой или бананом и озвучивают, используя союз «и». Но как бы мы его ни называли, смысл остается один: объединить основные причины и обозначить, что только в совокупности они формируют достаточное условие для наступления некоторого события.
Сравнительная значимость связанных причин
Если несколько причин необходимы для существования некоторого следствия, то нельзя говорить, что одни из них более важны, чем другие. Ведь для появления следствия нужны все причины, и исключение одной вызовет исчезновение самого следствия. Таким образом, каждая из имеющихся причин одинаково значима и достаточным условием будет наличие их в совокупности. Примечание «Сложные зависимости», данное после раздела «Альтернативная причина», освещает некоторые важные аспекты группирования причин.
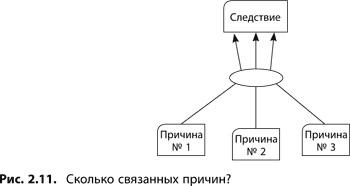
Сколько стрелок ставить?
Теоретически число стрелок, которые могут проходить через эллипс (т.е. количество взаимосвязанных причин, ведущих к одному следствию) не ограничено. Но на практике такое ограничение все же существует. В какой-то момент становится чрезвычайно сложно вычленить и отследить причины среди растущего числа стрелок. Кроме того, на определенном этапе число причин может значительно возрасти, а следствие каждой отдельной будет настолько мало, что им просто можно пренебречь.
Так сколько же стрелок можно объединить эллипсом? В каждом конкретном случае приходится полагаться на здравый смысл. Только вы сами можете определить тот момент, когда набор причин становится достаточным для наступления интересующего вас события. Однако старайтесь по возможности ограничить это число до трех, максимум до четырех (рис. 2.11). Когда причин больше четырех, сравнительное воздействие некоторых из них настолько мало, что их влиянием можно пренебречь. Наша задача — отобразить только те причины, без которых наступление события было бы малозаметным на фоне большой и сложной системы событий, или же те, без которых этого проявления не было бы вовсе.
Как правило, большинство следствий вызваны несколькими основными причинами. Если вдруг вам приходится включать в схему больше трех связанных причин одного следствия, тщательно изучите каждую из них. Некоторые могут оказаться независимыми, или альтернативными причинами (см. следующий раздел).
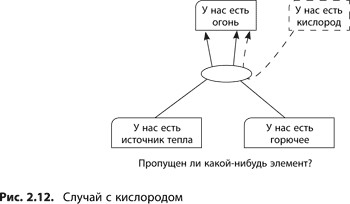
Случай с кислородом
Больше всего споров при обсуждении достаточности приведенной причины вызывают случаи, когда какая-либо причина (условие) является обязательной в данной ситуации и абсолютно очевидной только для разработчика логического дерева. Лучше всего продемонстрировать это на примере. Рассмотрим следующее утверждение, передающее причинно-следственные отношения: «Если у нас есть горючее и мощный источник тепла, то мы можем развести огонь» (см. рис. 2.12).
Не пропущено ли здесь что-нибудь? Специалист в области физики может возразить: «Вы забыли кое-что существенное — кислород. Без него возгорания не произойдет». В этом случае можно говорить о нарушении принципа достаточности причины.
На это можно ответить так: «Да, верно, но поскольку кислород всегда есть там, где я развожу огонь, я считаю его постоянной величиной, которую упоминать не нужно». Таким образом, случай с кислородом свидетельствует: иногда может иметь место фактор, который является очевидным для тех, кто обладает некоторыми знаниями в разбираемой ситуации, и фактор этот зачастую не упоминается в рассуждениях.
Однако докладчик должен быть готов к следующим комментариям:
опущенное условие («наличие кислорода») не очевидно для аудитории;
о причине нельзя просто догадаться, так как это скорее переменный фактор, который не является ни очевидным, ни постоянным в данной ситуации.
В этом случае составитель диаграммы должен быть готов пересмотреть и перепроверить предложенные им причинно-следственные связи.
Рисунок 8.4 «Построение диалога при помощи КПЛП» в конце главы 8 подробно разъясняет, как выявлять случаи несоблюдения принципа достаточности причины, а также реагировать на критику при анализе диаграмм. На рис. 2.13 дается пример и вопросы для проверки на достаточность причины.
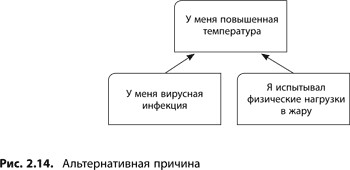
Альтернативная причина
Иногда явление может быть вызвано одной из нескольких независимых причин. Именно для выявления таких случаев необходима проверка на отсутствие альтернативной причины. Например, повышенная температура тела может быть вызвана внутренней инфекцией или же физическими нагрузками в жаркую погоду (см. рис. 2.14). Ключевыми здесь являются слова «или-или». т.е. при проверке на достаточность причины выявляются пропущенные причины с отношениями «и-и», а при проверке на наличие альтернативной причины — объединенные логикой «или-или». При проверке на альтернативную причину мы не ставим под вопрос приведенную в диаграмме причину, а лишь предполагаем, что может быть еще что-то, ведущее к таким же результатам.
Значимость
Найденная при проверке альтернативная причина должна приниматься во внимание, только если ее проявления сравнимы по масштабу с результатом первоначально заявленной. Например, в условиях экономического спада у всех могут на 10% сократиться продажи. Но если ваши продажи упали на 20%, должна быть еще какая-то другая причина, повлекшая за собой эти дополнительные 10%. Если результат, вызванный предполагаемой альтернативной причиной, значительно меньше результата, вызываемого исходной причиной, то дополнительная причина может быть исключена из рассмотрения. Масштабы вызываемого следствия, как и в случае с критерием достаточности причины, оцениваются в каждом конкретном случае на основании здравого смысла.
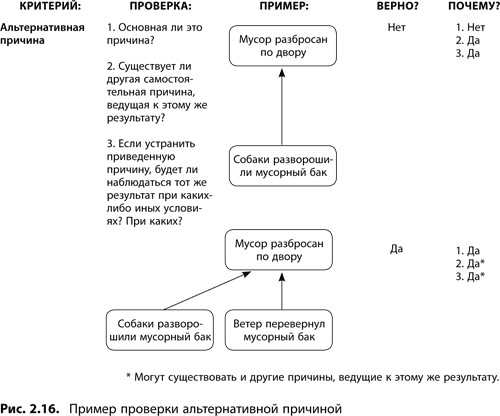
Проверка
Быстрее всего проверить отсутствие альтернативной причины можно, задав вопрос: «Если убрать исходную причину, будет ли наблюдаться тот же результат при каких-то других условиях?»
Особая
разновидность
альтернативной причины
Часто самостоятельные альтернативные причины сами являются составными. Например, три утверждения, объединенные эллипсом (т.е. в совокупности составляющие достаточную причину), будут считаться одной самостоятельной причиной. При этом события, вызываемые этой составной причиной, могут иметь еще и альтернативные независимые причины, которые также в свою очередь могут быть составными (см. рис. 2.15). Таким образом получается сложная картина взаимоотношений: составные причины, соединенные с одним и тем же следствием, между собой будут считаться альтернативными (логика «или-или»), а факторы, формирующие эти составные причины, объединенные эллипсом, между собой связаны логикой «и-и».
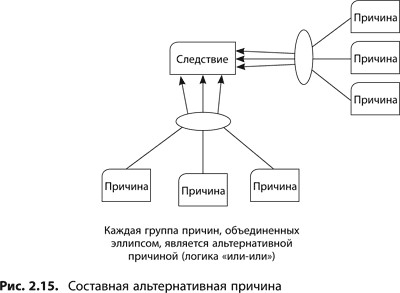
Рисунок 8.4 «Построение диалога при помощи КПЛП» в конце главы 8 подробно разъясняет, как проверять отсутствие альтернативной причины, а также реагировать на критику при анализе диаграмм. На рис. 2.16 дается пример и вопросы для проверки отсутствия альтернативной причины.
Назад: Как работать с этой главой
Дальше: Примечание: сложные зависимости

