1. Модели и методы финансово – экономических расчетов

Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Их используют вместо финансовых уравнений. Они работают быстрее, чем введенные формулы, и с меньшей вероятностью ошибок.

Количественный финансовый анализ предполагает применение унифицированных моделей и методов расчета финансовых показателей.

В этом контексте, Microsoft Excel предоставляет широкий спектр функций для финансово-экономических расчетов: от нахождения выплат по процентам, реализации задач дисконтирования, посторения моделей расчета амортизации оборудования, анализа показателей ценных бумаг, регулярных выплат по займу до оценки эффективности капитальных вложений и инвестиций, моделирования финансово-экономических аспектов деятельности предприятия, фирмы и т.п.

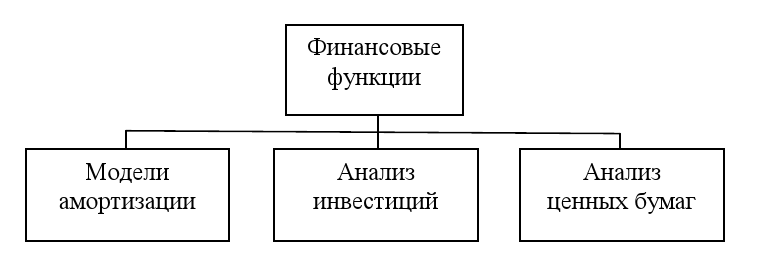
Рис. 1. Обобщенная классификация финансовых функций

Условно методы финансовой математики делятся на две категории: базовые и прикладные. К базовым методам и моделям относятся:

– простые и сложные проценты. Простые проценты используются, как правило, в краткосрочных финансово-экономических операциях (продолжительностью до года). Базой для исчисления процентов за каждый период в этом случае служит исходная сумма сделки. Сложные проценты применяются в среднесрочных и долгосрочных финансовых операциях (более одного года), но могут применяться и в краткосрочных, если это вызвано объективной необходимостью (риски, высокий уровень инфляции и т.п.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов;

– расчет последовательностей (потоков) платежей. При проведении большинства финансовых операций возникают чередующиеся в течение ограниченного или неограниченного промежутка времени поступления и выплаты денежных средств. Поток состоит из отдельных элементов потока – платежей. Поступление денежных средств считают положительными платежами, а выплаты – отрицательными. Денежные потоки делятся:

– по распределению во времени: регулярные (периодические) и нерегулярные;

– по величине элементов: на постоянные и переменные.

Наращенная сумма может представлять собой общую сумму накопленной задолженности к концу срока, итоговый объем инвестиций, накопленный денежный резерв и т.д.

Современная стоимость характеризует приведенные к началу осуществления проекта затраты, капитализированный доход или чистую приведенную прибыль от реализации проекта и т.д.

К прикладным методам финансовых расчетов относятся:

– планирование и оценка эффективности финансово-кредитных операций;

– расчет страховых аннуитетов;

– планирование погашения долгосрочной задолженности;

– планирование погашения ипотечных ссуд и потребительских кредитов;

– финансовые расчеты по ценным бумагам;

– лизинговые, факторинговые и форфейтинговые банковские операции;

– планирование и анализ инвестиционных проектов и др.

Особенностью всех финансовых расчетов является временная ценность денег, то есть принцип неравноценности денег, относящихся к разным моментам времени. Деньги – это мера стоимости товаров и услуг. Предполагается, что полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем, то есть будущие поступления менее ценны, чем современные. Неравноценность одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем.

Основными понятиями финансовых методов расчета являются:

– процент – абсолютная величина дохода от предоставления денег в долг в любой его форме;

– процентная ставка – относительная величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби, которая используется в качестве измерителя уровня (нормы) доходности задачу – нахождение величины на заданный момент времени по ее известному или предполагаемому значению в будущем.

Ввиду ограниченного объема данного учебного пособия, теоретические вопросы описания методов, расчетов, способов, определений, а также и другие характеристики рекомендуется изучать в специальной литературе [7].