СТРАТЕГИЯ 6

СМОТРЕТЬ НА ДРУГУЮ СТОРОНУ

При рассмотрении проблемы мы обычно предполагаем, что существуют определенные границы, в рамках которых и должно лежать решение. Очень часто, однако, оказывается, что границы воображаемые, а решение может находиться и за этими пределами. В 1872 году Рихард Дедекинд первым показал: математики обманывались, считая, что имеют дело с континуумом. По его доказательствам, для чисел континуума не существует. Внутри любого числового предела, например между 1 и 5, есть возможность вставить не­ограниченное количество чисел. К натуральным числам — 2, 3 и 4 — можно добавить бесконечное количество рациональных дробей типа ¾ или ¹¹⁸/₁₁₉, а также бесконечное количество чисел иррациональных, например квад­ратный корень из 2, и место останется в любом случае. Это открытие стало известно как принцип дискретности.

Дискретность быстро стала ключевой темой в модернизме и сформировала новый тип научного, художественного и изобретательского мышления. Физик Людвиг Больцман вскоре продемонстрировал, что непрерывность в физике — такая же статистическая иллюзия, поскольку поведение атомов непредсказуемо. Французский художник Жорж Сёра использовал этот тип мышления, вводя новый метод письма — пуантилизм. Первую современную картину — «Воскресенье после полудня на острове Гранд-Жатт» — он написал тысячами цветных точек, диаметр каждой из которых был не больше трех миллиметров. На этом шедевре изображены около 50 человеческих фигур, собаки и обезьяна, и все это сводится к мелким мазкам краски, которые каким-то образом формируют гармоничное целое, излучающее при этом невероятное спокойствие. Томас Эдисон изобрел кинокамеру, которая тоже стала триумфом дискретности: 16 неподвижных фотографий в секунду наш глаз интерпретирует как движение.

Смена направления

Дедекинд сумел увидеть другую сторону непрерывности, изменив направление своих мыслей о ней. Так родилась блестящая догадка, породившая новый способ мышления в науке и искусстве. Рисунок ниже состоит из неправильных фигур, которые выглядят бессмысленными кусочками пазла. Но если сконцентрироваться на фоне — пространстве между фигурами, — вы заметите слово ЗАПАД. Если вы все еще не видите его, приложите линейку к верхней или нижней границе фигур, тогда оно выступит более явно.

Сосредоточившись на отрицательном пространстве, а не на фигурах, вы изменили угол зрения и увидели то, чего не могли видеть раньше. Вот что бывает, когда меняешь направление обзора и смотришь на другую сторону вещей. Допустим, вам предстоит организовать одиночный теннисный турнир по олимпийской системе. Всего участников 117. Каково минимальное число матчей, которое необходимо организовать для этого количества участников?

Столкнувшись с этой задачей, большинство начнут чертить диаграммы с парами соперников для каждого матча и количеством пустых номеров. Другие попытаются решить задачу математически. Ответ, однако, прост: нужно 116 матчей, и выяснить это просто без всяких сложных расчетов и графиков. Чтобы прийти к нему, смените направление мысли и думайте не о победителях каждого матча, а о проигравших. Поскольку олимпийская система предполагает, что победитель должен быть один, проигравших будет 116. Каждый из них проигрывает лишь единожды, поэтому матчей должно быть 116.

Общая тенденция в этой задаче — сосредоточиваться на победителях, а не на проигравших. Изменение направления мышления подсказывает мысль о проигравших, а не о победителях, после чего задача быстро решается. Изменение взгляда на вещи позволяет принимать во внимание то, что иначе ускользнуло бы. В Средние века жители одной французской деревни умирали от «черной смерти». Их соседи обнаружили, что те по ошибке похоронили нескольких еще живых сограждан. Они сформулировали проблему так: нужно убедиться, что они не хоронят еще живых людей. Но кто-то с хорошим воображением решил проблему, перевернув задание. Он предложил убеждаться, что люди мертвы, еще до похорон, вонзая кол в крышку гроба. Изменение постановки проблемы изменяет и точку зрения.

Смена направления ломает существующие шаблоны, вызывая появление новых. Вы смотрите на предмет, а потом выворачиваете его наизнанку, вверх ногами, задом наперед. На рисунке фигура А состоит из двух линий равной длины, ограниченных стреловидными углами. На рисунке В стреловидные углы на одной из линий обращены в другую сторону, что меняет наше восприятие: кажется, что эта линия короче. Но это не так. Измерив ее, вы обнаружите, что она по-прежнему той же длины, что и остальные. Сами линии не изменились — поменялось их восприятие вами.

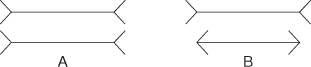
У фигуры А углы в конце линий словно открывают потенциально ограниченное пространство. Поворот угла внутрь, напротив, закрывает и ограничивает пространство, что и ведет к изменению восприятия длины этой линии.

Простой поворот угла полностью меняет то, что мы видим на иллюстрации. Те же изменения в восприятии происходят, если мы меняем направление наших обычных мыслительных шаблонов применительно к проблемам и ситуациям. Во времена, когда Генри Форд пришел в автомобильный бизнес, считалось правильным «доставлять людей на работу». Он пересмотрел этот подход, сделал своим девизом «доставку работы к людям» — и изобрел конвейер. Когда Эл Слоун стал генеральным директором General Motors, неоспоримым считалось, что нужно купить машину и уже потом на ней ездить. Он изменил это убеждение, заявив, что «можно ездить на машине еще до того, как за нее заплатишь», и стал пионером в области продаж автомобилей в рассрочку.

Несколько лет назад химики никак не могли решить проблему покрытия таблеток аспирина оболочкой с приятным вкусом. Погружение таблеток в раствор оболочки приводило к тому, что поверхность выходила неровная и комковатая. Они были в тупике, пока не изменили направление мышления. Вместо того чтобы думать о том, как поместить что-то «на» аспирин, они стали думать, как убрать нечто «с» аспирина. Эти изменения привели к открытию одного из новейших методов покрытия таблеток оболочкой. Таблетки вымачиваются в жидкости, а затем передаются на вращающийся диск. Центробежная сила, действующая на жидкость и таблетки, разделяет их, оставляя на последних симпатичное ровное покрытие.

Физик и философ Дэвид Бом считал, что гении могли мыслить иначе, чем остальные, потому что им не претила двойственность отношений между противоположными или несовместимыми предметами. Так, революционное изобретение Томасом Эдисоном реализуемой на практике системы освещения стало возможным благодаря параллельному подключению тока и использованию нити накаливания высокого напряжения в лампочках, что до того считалось невероятным и, честно говоря, вообще не рассматривалось из-за «очевидной» несовместимости. Так как Эдисону эта кажущаяся несовместимость нисколько не мешала, он смог разглядеть отношения, которые и привели к революционному открытию.

Эдисон всегда был рад бросить вызов традиционным представлениям, меняя в них акценты и стараясь все сделать наоборот. Есть такая интересная история о нем: каждый раз, проводя собеседование с человеком, желающим поступить к нему на работу, он приглашал того на обед и заказывал ему тарелку супа. Если претендент начинал сразу же, не пробуя, сыпать в суп соль или перец, Эдисон отказывал ему в трудоустройстве. Он считал, что у такого претендента слишком много устоявшихся взглядов на жизнь, так что заставить его думать творчески будет слишком сложно и займет чересчур много времени.

На иллюстрации вы видите четыре черные стрелки на белом фоне или же четыре белые стрелки на черном фоне. Можно сосредоточиться либо на черных, либо, наоборот, на белых стрелках. Сконцентрировавшись на черных, вы начинаете видеть белые, и наоборот. Точно так же любая мысль пробуждает свою противоположность — достаточно просто добавить слово «нет» или развернуть исходную мысль в обратную сторону.

Математик и философ Бертран Рассел однажды поразил коллег заявлением, что в математическом споре любая альтернатива ведет к своей противоположности. Вызвать к жизни новые идеи можно, рассмотрев противоположность любого предмета или действия. Когда биоинженеры искали способы улучшить качество помидоров, они открыли ген, ответственный за их созревание. Разработчики решили: если этот ген ускоряет созревание (черная стрелка), его, наверное, можно использовать и для замедления этого процесса, изменив вектор действия (белая стрелка). Они скопировали ген, обратили его действие вспять, и сейчас этот ген замедляет созревание, так что зимой помидоры спеют на кусте.

Инверсия предположений

Допустим, вы хотите открыть ресторан, но испытываете недостаток идей. Чтобы запустить мыслительный процесс, попробуйте следующие инверсии.

1. Запишите все свои предположения на эту тему.

   Пример: некоторые обычные предположения о ресторанах.

   • В ресторанах есть меню — письменные, устные или подразуме­ваемые.
   • В ресторанах за еду платят деньги.
   • В ресторанах подают еду.
2. Измените каждое предположение на прямо противоположное. Какова противоположность этому предположению?

   Пример: противоположные предположения были бы следующими.

   • В ресторанах нет никаких меню.
   • В ресторанах кормят бесплатно.
   • В ресторанах не подают никакой еды.
3. Спросите себя, как реализовать каждую инверсию.

   Пример: как можно открыть ресторан, в котором нет никакого меню, и все же это предприятие будет жизнеспособным?

   • Ресторан без меню.

     Идея: повар сообщает каждому клиенту, что купил в тот день на мясном, рыбном и овощном рынках. Он просит выбрать продукты, которые тому нравятся, и готовит из них блюдо специально для этого посетителя.

   • Ресторан, который раздает еду.

     Идея: уличное кафе, где клиенты платят за время, а не за еду. Отмечайте время и берите плату за каждую минуту. Выбранные блюда и напитки бесплатны или продаются по себестоимости.

   • Ресторан, в котором не подают еду.

     Идея: создайте ресторан с уникальной обстановкой в экзотическом окружении и сдавайте это место в аренду. Люди будут приносить свои продукты и напитки (корзины для пикника и т. д.) и платить за предоставление места.

4. Выберите одну из инверсий и воплотите ее в реалистичную идею.

Пример: мы решили поработать с инверсией «ресторан без меню». Назовем этот ресторан «Креативный повар»: повар создаст блюдо из выбранных ингредиентов и назовет его в честь клиента. Каждый клиент получит компьютерную распечатку рецепта. Инверсии нарушают устойчивые паттерны мышления, освобождают информацию, чтобы разные ее составляющие снова соединились новыми смелыми способами. Вот примеры.

• Допустим, у вас есть стакан мятного коктейля. Теперь представьте, что у мятного коктейля есть вы. Как это осуществить? Вообразите, что вы упали в стакан мятного коктейля. Это наводит на мысль о душе, совмещенном с различными запахами и ароматами.
• Водители следят за временем стоянки своих автомобилей. Пусть автомобили следят за временем стоянки. Это приводит к идее, что возможна парковка где угодно до тех пор, пока включены фары. Это может стать хорошей идеей для тех городов, где люди слишком часто надолго паркуют машины на главных улицах.
• У стоматологов есть специальные инструменты. Пусть этих специальных инструментов не будет. Как стоматолог может без них выполнить свою работу? Это приводит к идее, что пациенты купят собственные инструменты, которые стоматологи будут хранить в стерильных контейнерах, чтобы предотвратить передачу инфекции.
• Стул высокий. Пусть стул будет низким. Это приводит к идее, что можно использовать кусок толстого набивочного материала, положив его на что-то еще, возможно, большой камень или упавшее дерево, чтобы получился стул. На самом деле вы можете положить подушку поверх чего угодно, чтобы получился стул.

Скажем, два мальчика разного возраста и уровня мастерства играют в бадминтон. Старший мальчик играет намного лучше, чем младший, и выигрывает каждую игру. Младший обескуражен и отказывается играть. Так как это портит веселье старшему мальчику, встает вопрос: как удержать младшего в игре? Мысля стандартно, можно предложить, чтобы старший давал младшему фору или убедил его, что тот проиграл с честью. Но с помощью инверсии мы можем превратить игру в сотрудничество, задавшись целью увидеть, как долго эти два мальчика смогут удержать в игре волан.

Группы

Работая в небольшой группе, попросите каждого участника оформить свои предположения на заданную тему в нумерованный список. Далее можно:

• назвать произвольный номер, например три. После этого каждый участник делает инверсию своего предположения и ищет пути воплощения этой инверсии в жизнеспособной идее;
• попросить каждого участника выбрать одно предположение из своего списка и инвертировать его;
• предложить каждому участнику инвертировать все свои предположения;
• разрезать листы на полоски с предположениями и поместить их в бумажный пакет. Вынуть одну полоску и вместе с группой обдумать, как инвертировать это предположение в нечто новое. Продолжать доставать бумажки и инвертировать, пока не обретете нужные идеи.

Инвертирование дает много провокационных идей за сравнительно короткий срок. В одном примере менеджер крупной компании по производству копиров решила пересмотреть отношение своей организации к конкурентам — перейти от конфронтации к политике сотрудничества. Обычно в производстве копиров с конкурентами не сотрудничают никоим образом. Эта компания также не обслуживала машины конкурентов. Однако менеджер публично объявила, что ее компания не только будет проводить ремонт копиров конкурентов, но и обслуживать выданные ими гарантии. Такая политика имела громадный успех: это позволило установить отношения с клиентами конкурентов, что постепенно привело к большим продажам.

Инверсии дают возможность взглянуть на вещи двумя разными способами. Наилучший пример извлеченной из этого выгоды можно найти в математике. Любое уравнение — не более чем запись двух различных вариантов описания предмета, однако польза от описания числа двумя способами вместо одного настолько велика, что уравнение превратилось в один из краеугольных камней математики. Имея возможность двумя способами посмотреть на то, что находится по другую сторону знака равенства, можно легко найти ответ.

Обратная перспектива

Рассмотрим противоречие зеркала: почему оно так очевидно инвертирует левую и правую сторону, но не верх и низ? То есть почему буквы в книге перевернуты задом наперед, но не вверх дном, и почему в зеркальном отражении левая рука — это правая, а правая — левая?

Когда мы смотрим в зеркало, представляем себя перевернутыми слева направо, как будто прошли сквозь стекло, чтобы выглядеть иначе. Из-за традиционной точки зрения мы не можем объяснить, что происходит с зеркалом. Чтобы понять зеркальный образ, вы должны в психологическом отношении полностью изменить способ восприятия собственного отражения. Представьте, что ваш нос и затылок поменялись местами: если у вас нос направлен на север, то нос вашего двойника — на юг. Проблема состоит в оси, проходящей через зеркало. Вы должны вообразить себя перевернутым, или «вдавленным», задом наперед. Встаньте перед зеркалом, указывая одной рукой на восток, а другой — на запад. Махните «восточной» рукой. Отражение в зеркале машет «восточной» рукой. Его «западная» рука показывает на запад. Его голова вверху, а ноги внизу. Как только вы рассмотрите зеркало с такой парадоксальной точки зрения, вы поймете зеркальную ось.

Психологическое изменение способа восприятия своего отражения помогает понять зеркало. Таким же образом парадоксальное мышление может привести к новому пониманию или революционной идее. Например, нужно сложить числа от 1 до 100. Задача не самая сложная, но отнимает много времени. В итоге ответ есть: 5050. А теперь представьте, что числа от 1 до 100 записаны в ряд. Поменяйте порядок чисел и запишите их строчкой ниже, как в нашем примере:

1 2 3 4 5............95 96 97 98 99 100

100 99 98 91 96..............6 5 4 3 2 1

Записывая числа от 1 до 100, вы всегда прибавляете 1. Изменив направление и спускаясь от 100 к 1, единицу убавляете. При сложении каждой пары чисел всегда получается 101. Общее число — это 10 100, то есть 100 × 101. Мы использовали два набора чисел, так что разделим этот результат надвое и получим 5050. Итак, инверсия числового ряда позволяет визуально представить ряды чисел и понять последовательность. После этого можно в уме провести операции умножения и деления и быстро прийти к ответу, при этом риска ошибиться будет меньше, чем при обычном методе сложения.

Последнее время ученые стали смотреть в телескоп с другого конца, пытаясь под иным углом взглянуть на происхождение жизни. Вместо того чтобы пытаться объяснить, как появилась жизнь во Вселенной, они инвертировали задание: теперь жизнь — это данность, а задача обратная. Учитывая, что мы здесь и живы, изначальные условия должны обладать определенными свойствами. Пересмотр проблемы дает возможность сосредоточиться на другом ее аспекте. Если кого-то повысили в звании через вашу голову, вы можете подумать: «Дело в том, что босс меня не любит». Инвертировав это высказывание, получим: «Это произошло, потому что я не люблю босса». Не стала ли проблема яснее при таком взгляде на нее?

Инверсия может помочь найти истинные причины проблемы, которыми и стоит заняться. Например, представьте, что у вас падают продажи и вы хотите их увеличить. Вот как инвертировать проблему и определить истинные причины падения продаж.

1. Сформулируйте проблему.

   «Каким образом я могу увеличить продажи?»

2. Инвертируйте ее.

   «Каким образом я могу сократить продажи?»

3. Перечислите все способы, облегчающие реализацию такой инверсии.

   Пример: делайте меньше рабочих звонков, хамите клиентам, не оказывайте им поддержку, демонстрируйте плохое знакомство с продуктом и нежелание проводить гарантийное обслуживание и т. д.

4. Проведите оценку. Присвойте всем элементам списка числовое значение в соответствии с их важностью (1 — наименее важный, 10 — наиболее важный).
5. Сосредоточьтесь на элементах, получивших высшие оценки. Они и будут наиболее вероятными причинами ваших проблем.

   Пример: высшую оценку получил способ «делайте меньше рабочих звонков».

6. Вернитесь к исходной формулировке и поставьте более конкретный вопрос.

   Пример: «Каким образом я могу увеличить продажи, делая больше деловых звонков?»

Инверсия проблемы привела к пониманию того, что наиболее эффективный метод увеличения продаж — делать больше деловых звонков. Таким образом, реальная проблема состоит в том, как делать больше деловых звонков.

Обратный мозговой штурм

При мозговом штурме его участники пытаются придумать как можно больше идей, воздерживаясь от любых суждений или критики. Смысл в том, чтобы обеспечить среду для положительной обратной связи. В науке положительная обратная связь — это не всегда хорошо. Она часто приводит систему в негодность или заставляет ее выйти из-под контроля. Так, если направить телевизионную камеру на ее собственный монитор, с изображением получится примерно то же самое, что и со звуком, если микрофон расположить слишком близко к колонкам.

Вот почему ученые подчеркивают разницу между двумя типами обратной связи. В науке именно «отрицательная обратная связь» помогает держать все под контролем: клапан паровой машины Уатта создавал цикл отрицательной обратной связи, потому что открывался, когда машина двигалась слишком быстро, и предотвращал ее возможный взрыв или выход из-под контроля. В природе отрицательная обратная связь в эволюции держит под контролем мутационные изменения: многие мутации оказываются нежизнеспособными, и общие признаки вида остаются стабильными в течение длительных периодов.

Обратный мозговой штурм — это критическая оценка или суждение об идеях, при котором поощряется отрицательная обратная связь. Особенно полезен этот метод, если группа заинтересована преодолеть все возможные слабости конкретной идеи. Цель — определить слабости, дав участникам задание воспрепятствовать реализации намеченного плана и выявить возможные способы этого. Представьте, например, что ваша компания разработала пятилетний план вывода на рынок беспроводного телефона. Чтобы начать процесс обратного мозгового штурма, нужно следующее.

1. Разбить группу на отдельные команды. Каждая команда должна действовать как конкретный конкурент (или же можно предложить командам создать мифического суперконкурента). Сообщите участникам, что произошла утечка информации и стал известен новый маркетинговый план вашей компании. В качестве ответа на новую угрозу им (конкурентам) необходимо разработать эффективные контрмеры.
2. Каждая группа проводит мозговой штурм контрмер, препятству­ющих реализации плана.
3. После этого группа вновь объединяется и обсуждает контрмеры конкурентов. Группе предлагают выработать реакции на каждую из таких контрмер. Инвертирование мышления создает новые мысли­тельные шаблоны, которые приводят к идеям, обычно вообще не рассматриваемым.

Техника смены направления порождает двойственность — фундаментальное, но редко принимаемое во внимание свойство творческой мысли. Гении легко мирятся с двойственностью: пример тому — полярность мышления Эйнштейна. Он то становился на сторону континуума, то предпочитал дискретность. Ему были видны отношения между этими явлениями, потому что он не отвергал ни одно из них. Любая непрерывная система может быть представлена как сочетание дискретных элементов. Любой дискретный элемент состоит из непрерывного фона. Эта способность мириться с двойственностью дает гениям доступ к таким нюансам, на которые обычные люди, думающие шаблонно, редко обращают внимание.

Видеть все стороны

Доктор Альберт Ротенберг, известный исследователь творческого процесса, уже долгое время изучает использование в нем противоположностей. Он выявил составляющую творчества, которой дал название «янусово мышление»: в честь Януса — римского бога с двумя лицами, смотрящими в противоположных направлениях. Янусово мышление — это способность одновременно представлять две противоположные или противоречащие друг другу идеи, два понятия или образа. Это как, например, ваша мама одновременно существует в образе младенца и пожилой женщины, а у вас одновременно и есть домашнее животное, и нет его.

Ротенберг выяснил, что гении довольно часто прибегали к мышлению такого рода, обретая оригинальные концепции. Эту способность демонстрировали Эйнштейн, Моцарт, Эдисон, Ван Гог, Пастер, Конрад и Пикассо. Именно Винсент Ван Гог на картине «Спальня в Арле» впервые показал, как можно в одно и то же время видеть вещи под двумя разными углами зрения. Кубистское мышление художника выражалось в том, что он расчленял объекты в воображении, а затем перекомпоновывал их элементы, так что объект представал словно запечатленным с десятка углов зрения. Шедевр «Авиньонские девицы» — возможно, первая в западном искусстве картина, изображающая предметы со всех сторон одновременно. Наблюдатель, который хочет ее оценить, должен увидеть в один момент все точки зрения. Иными словами, чтобы оценить красоту одновременности, вы должны смотреть на предмет точно так же, как сам Пикассо.

В физике Эйнштейн мог в одно и то же время представлять объект в движении и в покое. Чтобы лучше осознать природу этого парадокса, он предложил аналогию, отражающую его суть. Физик указывал, что наблюдатель, который прыгнул с крыши и одновременно выпустил из рук какой-либо предмет, сочтет, что предмет по отношению к нему продолжает находиться в состоянии покоя.

Эйнштейн понимал, что прыгающий с крыши наблюдатель в своих координатах не обнаружит никакого свидетельства существования гравитационного поля. Это кажущееся отсутствие возникает даже несмотря на то, что именно гравитационное поле и ускоряет падение наблюдателя. Ученый говорил, что эта аналогия была самой счастливой идеей в его жизни, поскольку именно она вызвала к жизни более серьезную идею — общую теорию относительности. (Эйнштейн искал в природе аналогию, позволяющую внедрить теорию гравитации Ньютона в теорию относительности, чтобы та стала носить всеобщий характер.)

Луи Пастер открыл основной принцип иммунологии, наткнувшись на парадокс: некоторые зараженные холерой цыплята выживали. Когда их и здоровых птенцов заражали новым вирусом, то незараженные цыплята умирали, а зараженные вновь выживали. Увидев в неожиданной жизнестойкости цыплят проявление общего принципа, Пастер понял необходимость формулировки концепции, при которой выжившие птенцы были заражены и одновременно не заражены. Не отмеченная до этого инфекция каким-то образом спасала их от заболевания и смерти в результате нового заражения. Парадоксальная идея того, что имеющееся заболевание может предотвращать новые болезни, стала исходной для создания иммунологической науки.

Ротенберг обнаружил пример янусова мышления и в работах Нильса Бора. Бор считал, что, если вы одновременно держите в уме противоположные друг другу идеи, мышление переходит на новый уровень. Такое «подвешенное» мышление позволяет разуму действовать, создавать новые формы. Борьба противоположностей формирует условия для выработки новой точки зрения. Именно эта способность учитывать одновременно обе противоположности привела Бора к открытию принципа комплементарности — на первый взгляд противоречащему самому себе утверждению, что свет одновременно и волна, и частица.

Чтобы одновременно думать о противоположных понятиях, превратите тему размышлений в парадокс, а затем попытайтесь найти полезную аналогию.

В литейном производстве металл очищается пескоструйным способом. Однако песок, хотя и очищает металлические части, забивается в полости, и на удаление его оттуда уходит много времени и средств. Парадокс в том, что частицы должны быть «твердыми», чтобы очищать деталь, и «нетвердыми», чтобы можно было их легко извлекать. Аналог подобных «твердых» и «нетвердых» частиц — лед. Одно из решений, таким образом, — проводить очистку сухим льдом. Твердые частицы очистят детали, а затем случатся возгонка и испарение.

Допустим, вы хотите заработать кучу денег. Обратная сторона этого в том, что у вас мало амбиций. Парадокс: вы хотите зарабатывать деньги, но слишком ленивы, чтобы многое для этого сделать. Найдите аналогию, содержащую суть такого парадокса: например, я хочу получать свет, не используя электроэнергию. Решением будет применение естественной энергии Солнца. Теперь приложите этот принцип к проблеме лентяя, который хочет заработать деньги. Одно из решений — отправиться на южные острова и написать книгу о путешествии.

Парадоксальное мышление

Далее следуют конкретные принципы решения проблем путем создания парадокса, нахождения аналогии и использования ее уникальных свойств для выработки оригинальных идей.

Генеральный директор заметил, что, когда его компания высоких технологий была небольшой, люди часто спонтанно и неофициально встречались. Во время этих встреч появлялись лучшие идеи. В результате быстрого роста компании подобное общение (и число хороших идей) сократилось. Он пробовал использовать обычные способы стимулирования креативности (собрания, обеды, вечеринки, круглые столы и т. д.), но они не помогали генерировать новые идеи. Директор хотел воссоздать спонтанную творческую обстановку.

1. Парадокс. Превратите проблему в парадокс. Одно из различий между творческими и обычными людьми заключается в их толерантности к противоположностям. Например, физик Нильс Бор был восхищен, когда обнаружил парадокс, согласно которому свет можно назвать и частицей, и волной. Это противоречие привело к открытию принципа дополнительности, за которое он получил Нобелевскую премию. Нужно спросить себя: какова противоположность проблемы? Затем вообразить, что и то и другое существует одновременно.

   Пример: парадокс ситуации, в которой оказалась компания, состоял в том, что, если собрания не были спонтанными и неорганизованными, они не способствовали появлению новых идей.

2. Название книги. Резюмируйте парадокс в названии книги, охватывающем сущность и противоречие проблемы. Название должно состоять из двух слов, обычно из существительного и определения. Вот примеры таких заглавий:
   • цель продаж: «Сфокусированное желание»;
   • работники разного уровня: «Сбалансированный беспорядок»;
   • сезонные циклы продаж: «Взаимосвязанные паузы»;
   • регулирование рождаемости: «Надежные перебои»;
   • природа: «Рациональная импульсивность».

   Пример: в нашем случае генеральный директор резюмировал парадокс в названии книги «Неорганизованные собрания».

3. Аналогия. Найдите аналогию, отражающую сущность парадокса. Придумайте как можно больше аналогий и выберите наиболее подходящую.

   Пример: генеральный директор нашел подходящую аналогию в природе. Он подумал о серебристых чайках, которые очень неорганизованно питаются отбросами, но успешно выживают.

4. Уникальная особенность. Какова уникальная особенность этой аналогии? Творческие идеи часто предполагают применение уникальных особенностей одного предмета к другому.

   Пример: генеральный директор решил, что уникальная особенность его аналогии состоит в питании отбросами. Чайки собираются ради легкой добычи, когда рыбаки выбрасывают ненужную рыбу и куски рыбы назад в море.

5. Эквивалент. Используйте эквивалент этой уникальной особенности, чтобы прийти к новому пониманию.

   Пример: эквивалент этой уникальной особенности мог бы состоять в том, чтобы заставить людей собираться вместе ради приличной, но недорогой еды.

6. Новая идея. Компания будет продавать недорогие деликатесные блюда в своем кафе. Дотируя стоимость деликатесной пищи, генеральный директор поощрит служащих собираться в кафе (подобно серебристым чайкам, привлеченным легкой добычей), чтобы в не­официальной обстановке пообщаться и обменяться идеями.

Уильям Гордон использовал эту стратегию для разработки чипсов Pringles. Перед компанией стояла задача создать новые картофельные чипсы и более эффективную упаковку, которая не потребует заполнять пакет количеством воздуха, превышающим объем самих чипсов. Парадокс состоял в том, что чипсы должны быть упакованы более компактно и при этом не ломаться. «Название книги», выражающее суть этого парадокса, было «Компактная неразрушаемость».

В качестве аналогии они выбрали укладку опавших листьев в мешок осенью. Когда вы пытаетесь засунуть сухие листья в полиэтиленовый пакет, сталкиваетесь с определенными трудностями. Но когда листья сырые (уникальная особенность), они мягкие и легко изменяют форму. Влажный лист принимает форму соседнего листа, оставляя лишь немного воздуха между ними. Смачивание и формовка сухой картофельной муки позволили решить проблему с упаковкой, и это положило начало чипсам Pringles.

В другом примере дизайнеры разрабатывали гибкую батарейку, которую можно было свернуть, как лист бумаги. Они начали с парадокса «твердой эластичной батарейки». Название книги звучало как «Бетонная эластичность». Аналогией оказались «мешки для мусора», а уникальной особенностью — то, что «мешки наполнены высокосортной пластмассой». Эта аналогия привела к идее внедрения жидкого электролита в инертную полимерную пластинку. Таким образом удалось создать ультратонкую гибкую батарейку, которую можно сворачивать и разворачивать, как пластиковый пакет. Батарея может использоваться в звукозаписывающей аппаратуре, мобильных телефонах, ноутбуках, пейджерах и игрушках. Можно даже создать «ткань на батарейках», способную заряжать медицинские аппараты.

Думать в обратную сторону

Большинство из нас привыкли превращать вопрос (2 + 2 = ?) в ответ (4), соответствуя жесткому набору правил. Если вы, проходя мимо чьего-то стола, увидели калькулятор, на котором высвечивается 4, вы никогда не узнаете, результатом каких вычислений стала эта цифра. Что это было: 2 + 2, 3 + 1, 1 + 1 + 1 + 1, а может, 9 – 5 или 1239477 – 1239473? Способов получить в итоге 4 бесконечное множество.

Эйнштейн, как известно, представлял свою теорию относительности как данность и затем работал в обратную сторону — к тому, что было уже известно. Фрэнсис Крик и Джеймс Уотсон поразили научную общественность способом открытия структуры ДНК. Пока их коллеги пытались пойти по прямому и тесному пути логических умозаключений (то есть начали с 2 + 2), Крик и Уотсон сделали несколько смелых предположений (начали с 4), потом стали думать в обратную сторону, что и принесло плоды. Задание для следующей иллюстрации: как можно связать девять точек одной прямой линией, не отрывая карандаша от бумаги?

Эта задача большинству людей кажется нерешаемой. Многие воспринимают как данное саму задачу и пытаются решить ее, но безуспешно. Но если вы представите решение и начнете думать в обратную сторону, обнаружите, что решение довольно простое. Ниже приведено одно из таких решений.

Теперь вернитесь к проблеме и поищите способы достижения этого решения. Например, можно вырезать точки, наклеить на лист, вытянув в прямую линию, и затем эту прямую линию начертить. Можно также представить себе очень толстую линию, которая проходит сразу через все точки. После этого достаточно просто замазать широкой кистью точки. Эти творческие решения, возможно, не пришли бы нам в голову, если бы мы работали с задачей общепринятыми способами.

Представив, что проблема уже решена, вы получаете возможность подойти к ней с другой стороны и работать в противоположном направлении. Такой способ позволяет более гибко воспринимать проблему, изменяя ее компоненты. Вот правила того, как можно думать в обратную сторону.

1. Закройте глаза, расслабьтесь и представьте наилучшее решение вашей проблемы. Пусть вас ничто не стесняет: вы можете выдумать абсолютно любой вариант.
2. Запишите искомое на листе бумаги. Добавьте краткое описание того, какую выгоду вы из него извлечете, как будете себя чувствовать и какие силы после этого придут в движение.
3. Перечислите людей, ситуации, события, благодаря которым выдуманное решение стало возможным.
4. Опишите, как этот человек (ситуация, событие) повлиял на исход дела.
5. Спросите себя, что именно произошло, в результате чего решилась проблема? Можно ли предложить альтернативные решения?
6. Перечислите характеристики и свойства явлений, которые привели к разрешению проблемы. Видите ли недостатки? Если да, то как можно их преодолеть и улучшить решение?
7. Какие пробелы надо заполнить, прежде чем найти вариант? Как именно их следует заполнять? Что еще нужно знать?
8. Продолжайте спрашивать о том, что должно предшествовать каждому шагу, пока не дойдете в этом обратном направлении до исходной формулировки проблемы.

Традиционное мышление предполагает, что вы совершаете по одному шагу за раз. Каждый шаг прямо вытекает из предыдущего. Когда же вы думаете «в обратном направлении», шаги не следуют друг за другом: вы резко перепрыгиваете к решению, после чего заполняете пробелы. Ниже на диаграмме представлен сначала традиционный способ мышления — методичный переход от А к В, затем к С, D и, наконец, к решению Е. Применив же «мышление в другом направлении», вы находите идеальное решение — G, к которому, возможно, не смогли бы прийти обычными способами. Затем возвращаетесь к А, чтобы понять, как же отыскать решение. Начиная обратный путь от G, мы приходим к С, потом к D, Н и, наконец, к А. Это движение непоследовательное, оно включает такие шаги (Н), которые вы могли упустить, думая традиционно.

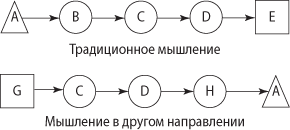
Никола Тесла — гений эпохи электричества — часто представлял решение проблемы как данность и мыслил в обратном направлении, двигаясь к вопросу. Например, работая над созданием турбин, он представил уже готовую турбину и дошел до этой стадии «мысленно» всего за месяц. Для Теслы не имело значения, придумал он что-то или дошел до решения благодаря физической проверке в лаборатории. Через месяц он так же мысленно разобрал машину и в точнейших деталях описал изнашивание своего воображаемого механизма. Позже на основе его воображаемой турбины была построена и запущена настоящая, а через месяц ее разобрали. Поразительно, но описание Теслой износа деталей механизма совпало в мельчайших подробностях.

Способность представлять будущее позволяла ему создавать поразительные, меняющие мир устройства, о которых раньше никто не задумывался даже теоретически. Изобретение Теслой вращающихся магнитных полей послужило основой для переменного тока, сделавшего возможным широкое использование электричества. Тесла заложил также основы робототехники, компьютерных технологий и ракетостроения, помог проложить путь к таким технологиям космической эры, как спутники, микроволновые печи, лучевое оружие и ядерная энергия. Некоторые эксперты даже предполагают, что программа стратегических оборонных инициатив Рональда Рейгана стала результатом секретных исследований, основанных на открытиях Теслы, которые были сделаны полувеком ранее.

Представив будущее, полное сверкающих огней, которые запускаются электрогенераторами; роботов, производящих революцию в промышлен­ности; всемирных коммуникаций, основанных на невидимых магнитных волнах, Тесла сумел проложить обратный путь от идей будущего, существующих в его воображении, к настоящему. Такое мышление в обратном направлении открыло его разум для бесчисленного количества самых разнообразных способов воплотить задумки в жизнь.

Например, вы работаете над некой проблемой в мире будущего. Затем перенесите решение обратно в настоящее и найдите способы превратить отдаленную идею в повседневную возможность. Вот основные правила.

1. Выберите дату в будущем (2050) и представьте, что вы живете в этом году. Придумайте несколько газетных заголовков в новостях о правительствах, частной жизни, технологиях, вашей компании и конкурентах. Напишите короткий рассказ — один день из жизни обычного человека в 2050 году.
2. Составьте список самых важных событий, которые к 2050 году будут связаны с вашей проблемой. Задайте такие вопросы: «Что из этого невозможно сейчас, но будет возможно к 2050 году? Чем я не обладаю сейчас, но что буду иметь в 2050 году? Какими ресурсами и какой информацией я смогу пользоваться?»
3. Используя эти возможности, представьте лучшее из возможных решений проблемы. Запишите его как можно более подробно. Затем перечислите людей, ситуации и события, повлиявшие на воплощение этого решения, и укажите, как именно это произошло.
4. Задайтесь вопросом, что в конечном счете привело к решению проб­лемы. Можно ли придумать альтернативы? Перечислите характеристики и свойства явлений, способствовавших разрешению проблемы. Перевод тематики размышлений в будущее позволяет поместить ее в другой контекст и создает новые отношения между компонентами проблемы. Осознание этих новых отношений и есть то, что подразумевается под догадкой.
5. Ищите недостатки. Если они есть, можно ли их преодолеть? Какие пробелы нужно заполнить, чтобы прийти к решению?
6. Продолжайте спрашивать о том, что должно предшествовать каждому шагу, пока не дойдете в этом обратном направлении до исходной формулировки проблемы. Возвращаясь таким образом из будущего, можно понять, какие условия должны были предшествовать желаемой цели, и установить, какие конкретные действия нужно предпринять для возникновения этих условий. Допустим, мы хотим отправиться на поезде из Милуоки в Бостон. Лучшей стратегией не обязательно окажется анализ железнодорожного расписания из Милуоки в Чикаго, из Чикаго в Буффало, из Буффало в Нью-Йорк и уже из Нью-Йорка в Бостон. Вместо этого можно узнать, какие поезда приходят в Бостон с запада в то время, когда мы хотели бы туда прибыть. После этого можно посмотреть, когда эти поезда уходят из, например, Буффало или Нью-Йорка, а затем спланируем поездку до Чикаго.

Группы

Групповое упражнение, направленное на рассмотрение участниками желаемой ситуации в будущем, предусматривает деление группы на три или четыре команды, каждая из которых разрабатывает воображаемое решение. Все решения раскладываются по разным конвертам. Каждая команда получает конверт с одним из возможных вариантов; записывает, какие действия нужно немедленно предпринять, чтобы добиться такого решения, и тоже вкладывает эту запись в конверт. Конверты передаются от группы к группе. Каждая группа придумывает действия самостоятельно, не глядя в записи других. Когда все группы обработали все варианты, руководитель зачитывает действия, предложенные командами. Группа обсуждает их и расставляет приоритеты.

Идеальная чашка кофе

Еще один способ думать в обратную сторону, начиная с решения, состоит в том, чтобы сначала придумать идеальное решение, перечислить существенные факторы, которые могут сделать его возможным, а затем составить таблицу, показывающую, где вы находитесь в данный момент и что необходимо сделать, чтобы идеальное решение стало реальностью. Например, я решил сварить «идеальную» чашку кофе. Сначала найду определение идеальной, по моим представлениям, чашке кофе. Это будут те самые существенные факторы для идеальной чашки кофе, которая будет обладать для меня наилучшим вкусом. Чтобы сварить эту идеальную чашку, мне понадобятся:

• лучшая в мире кофеварка;
• лучшие сорта от лучших производителей;
• хорошие знания о том, как варить кофе;
• самая чистая ключевая вода;
• самый чистый сахар;
• самые свежие и жирные сливки.

Далее я записываю антонимы ко всем этим существенным факторам, чтобы получить континуум, и свожу в следующую таблицу:

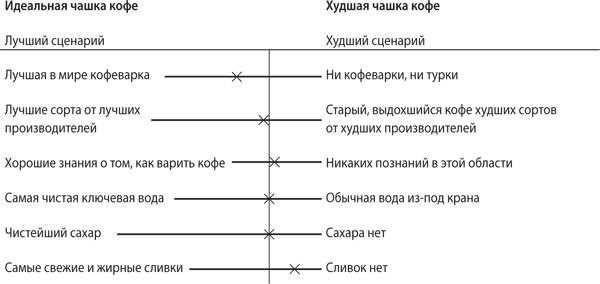
Я ставлю крестик на континууме (вертикальная линия обозначает сере­дину между двумя крайностями), отмечая, где нахожусь в это время. Например, крестик для кофеварки означает, что мой агрегат чуть выше среднего; я исполь­зую сорта кофе чуть выше среднего уровня, знаю чуть меньше среднего человека о том, как варить кофе, использую среднего качества воду и сахар, а вместо сливок добавляю молоко.

Подобная схема иллюстрирует, что я должен сделать, чтобы приблизиться к «идеальной» чашке кофе. Мне нужно приобрести кофеварку мирового класса, лучшие сорта кофе, чистейший сахар, свежайшие сливки, использовать ключевую воду и либо изучить вопрос варки кофе самому, либо пригласить специалиста, чтобы он меня научил. Я могу попробовать передвинуть один или несколько крестиков по направлению к «идеалу» или же оставить все как есть.

Это побудило одного предпринимателя изобрести идеальную чашку кофе для кофеварки. Она делает напиток, который может соперничать с предлагаемым в лучших кофейнях. Вместе с кофеваркой предприниматель рекомендует лучшие зерна, которые машина сама перемалывает, затем она отсчитывает строго определенный объем воды, очищает ее от загрязнений и варит кофе при нужной температуре. У кофемашины есть такие полезные функции, как воздухонепроницаемая пробка, защищающая от воздействия кислорода (и препятствующая появлению горечи), механизм самоочищения и таймер.

Посмотрите на иллюстрацию, на которой девушка стоит под дождем. А теперь попытайтесь представить ее полностью вписанной в меньший круг. Скорее всего, вы увидите, что изображение сжалось, так что можно различить лишь некоторые детали. Теперь перенесите изображение в большой круг. Рисунок стал четче, и вы видите гораздо больше подробностей.

Расширение мысленного образа позволило «увидеть» больше черт. Точно так же, представляя идеальное или совершенное решение проблемы, вы значительно расширяете свое восприятие этой проблемы. Дело в том, что мысленное восприятие во многом обладает теми же механизмами переработки информации, что и человеческое зрение. Ваше первоначальное понимание ситуации выглядит мелким и узким, как изображение в маленьком кружке. Расширение восприятия через представление идеального решения помогает заметить черты и компоненты, необходимые для реализации совершенного решения, как изображение в большем кругу.

Отправить