Глава III
АБСТРАКТНЫЙ УСИЛИТЕЛЬ

Для начала заглянем в энциклопедический словарь и найдем там такое пояснение: «Абстракция — мысленное отвлечение от тех или иных конкретных сторон, свойств или связей предмета. Научная абстракция — отвлечение от несущественных, случайных признаков предмета или явления в целях познания наиболее существенных его сторон…»

Сейчас мы начинаем серьезное знакомство с транзисторными усилителями. Начинаем не с каких-либо конкретных, а именно с абстрактных, обобщенных, «очищенных» от подробностей транзисторных схем. На этих схемах в коллекторную цепь транзистора вместо определенного резистора на 1,5 или на 4,3 килоома будет включен абстрактный, без конкретного значения резистор R_н. Между базой и эмиттером вместо конкретного, точно отмеренного напряжения 0,2 или 0,15 в, будет действовать абстрактное напряжение U_аб без указания величины. Да и сами транзисторы на таких схемах — это не конкретные приборы П13 или П403, а условные, абстрактные полупроводниковые триоды, без определенных названий и параметров.

Вам, по-видимому, хочется узнать, для чего понадобилось такое отвлечение от «конкретных сторон, свойств или связей» нашего «предмета» — транзисторного усилителя? И почему нельзя знакомиться с транзисторными усилителями не по абстрактным, а по конкретным схемам, которые в заключение знакомства можно было бы «спаять» и «пустить в дело»? Пусть таких практических схем очень много, пусть знакомство с ними дело долгое и утомительное, но ведь лучше сразу затрачивать силы и время на нужное, практически важное дело, чем заниматься какими-то абстракциями!

В качестве ответа на эти вопросы и возражения приведем такое сравнение.

Существуют очень сложные арифметические задачи, которые можно решать «обычным способом» — последовательно придумывать простые вопросы и отвечать на них вычислениями.

А можно решать эти задачи и по-другому — с помощью алгебраических уравнений. Вы, наверное, по собственному опыту знаете, что этот второй путь более удобен и легок. А главное, научившись решать абстрактные, то есть отвлеченные от конкретных чисел алгебраические уравнения, вы тем самым сразу получаете ключ к решению бессчетного множества разнообразных арифметических задач. К тому же этот алгебраический ключ открывает вам доступ к решению таких сложных задач, которые арифметическим способом практически вообще не решаются.

Можно смело сказать, что способность к абстрактному мышлению, умение выделять главные, наиболее важные особенности предметов и явлений, умение находить универсальные методы, пригодные для решения сразу многих сложных задач, пользоваться одним обобщенным, абстрактным понятием вместо огромного множества конкретных, — все это составляет одну из главных особенностей человеческого ума. Постарайтесь найти время и серьезно задуматься над этим.

А сейчас нам пора возвращаться к транзисторным схемам. Познакомившись с абстрактным усилителем, соединяющим в себе главные особенности множества конкретных транзисторных схем, познакомившись с характерными для этого абстрактного усилителя физическими процессами и схемными решениями, мы с вами вместо долгой и утомительной осады совершим своего рода танковый прорыв, — быстро и легко войдем в огромную и прекрасную Страну Практических Транзисторных Схем.

Мастера, ремонтирующие приемники или телевизоры, любят говорить, что радиоэлектроника — это наука о контактах. Действительно, нарушение контактов в переключателях, соединительных фишках, контактных разъемах, ламповых панелях, наконец просто в местах плохой пайки — это довольно частое, если не самое частое повреждение аппаратуры. Устранить такое повреждение несложно, но обычно требуется большой опыт, чтобы найти место нарушения контакта.

И все же изречение «Радиоэлектроника — наука о контактах» не более чем шутка. Если говорить серьезно, то радиоэлектроника — это прежде всего наука об электрических цепях и сигналах.

Если вы свободно разбираетесь в сложных электрических цепях, знаете законы, которым они подчиняются, представляете себе, как проходят по этим цепям различные электрические сигналы, то вы легко разберетесь в работе любого радиоэлектронного устройства. Любое радиоэлектронное устройство — это прежде всего электрические цепи, в которых создаются и преобразуются электрические сигналы.

Все сказанное в полной мере относится и к транзисторным усилителям. И именно поэтому, прежде чем браться за схемы усилителей, мы с вами устроим небольшой вечер воспоминаний — вспомним несколько важных правил, действующих в мире электрических цепей и сигналов. С некоторыми из этих правил вы уже встречались в этой книге, некоторые наверняка знаете с еще более давних времен. Ну, а если не знаете, то сможете узнать, познакомившись с одним из популярных учебников по основам электротехники. А на первых порах вам будет достаточно тех более чем скромных сведений, которые вы почерпнете из наших коротких воспоминаний. При этом не забывайте о примечании на стр. 26.

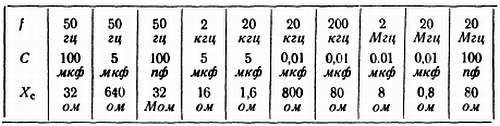
О первых трех характеристиках мы уже говорили на стр. 18. Известны также единицы, в которых измеряются сопротивление, напряжение и ток. Часто бывает удобно пользоваться более крупными и более мелкими единицами (не всегда же мы пользуемся метром — расстояние между городами удобней измерять в километрах, а диаметр провода — в миллиметpax). Как образуются производные единицы, все эти мегомы (Мом), килоомы (ком), миллиамперы (ма), микровольты (мкв) и другие, подскажет вам таблица.

Напряжение, которое может дать генератор в режиме холостого хода, то есть когда от него не потребляют энергии, называется электродвижущей силой, сокращенно э. д. с. Она, как и напряжение, измеряется в вольтах и так же говорит о работе, которую мог бы выполнить генератор, перемещая по цепи заряд в один кулон. Однако э. д. с. — это, откровенно говоря, хвастовство. Как только вы подключите к генератору нагрузку и в цепи пойдет ток, некоторая часть э. д. с. тут же потеряется на внутреннем сопротивлении этого генератора (см. стр. 146). Поэтому напряжение на зажимах генератора всегда меньше, чем э. д. с.

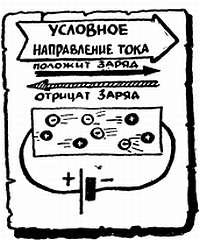
Разбирая сложные схемы, нужно следить, где возникает «плюс», где «минус», куда идет ток и т. д. Ток могут создавать и положительные, и отрицательные заряды, которые, естественно, под действием одного и того же напряжения движутся в разные стороны. Положительные заряды всегда тянутся к «минусу», а отрицательные бегут от него. Чтобы не заводить лишней путаницы, договорились следить только за движением положительных зарядов, а на отрицательные (электроны), по возможности, вообще не обращать внимания. Поэтому официальное направление тока — от «плюса» к «минусу».

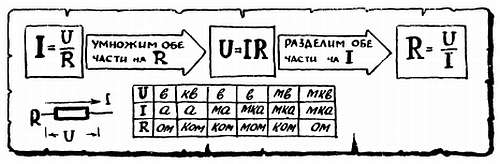
И о нем мы уже говорили не раз. Чтобы не допускать обидных ошибок при расчетах по формулам закона Ома, пользуйтесь приведенной здесь таблицей, в одном из вертикальных столбцов которой вы найдете удобный «комплект» единиц. Если цепь состоит из большого числа элементов, то нужно сначала найти ее общее сопротивление, которое позволит определить общий ток, а затем ток и напряжение на отдельных участках.

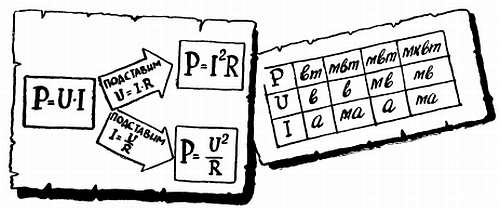
Как известно, мощность — это произведение тока на напряжение. Если неизвестна одна из этих величин, ее легко получить, пользуясь все тем же законом Ома. «Комплекты» единиц для вычисления приведены в таблице.

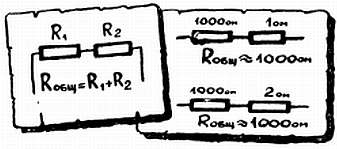
Общее сопротивление равно сумме соединенных сопротивлений, причем главную роль играет наибольшее из них.

ВОСПОМИНАНИЕ № 6. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ СОПРОТИВЛЕНИЙ.

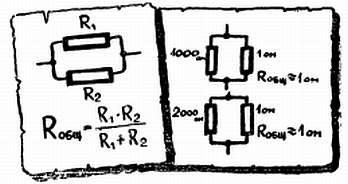
Общее сопротивление в основном определяется малым сопротивлением, а роль мухи достается большому.

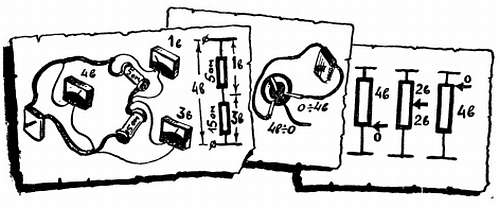
Подведем напряжение к двум последовательно соединенным резисторам. Оно автоматически распределится между ними так, что на большем сопротивлении будет действовать и большая часть напряжения.

Такое распределение напряжений легко объяснить. Дело в том, что во всех участках последовательной цепи течет один и тот же ток: сколько зарядов входит в электрическую цепь (не забывайте о примечании на стр. 26), столько же выйдет из нее. А чтобы продвинуть один кулон по участку с сопротивлением 10 ому нужно поработать в десять раз больше, чем для продвижения этого же кулона по участку с сопротивлением 1 ом.

Напряжение, ток, сопротивление на любом участке делителя, так же как и во всей цепи, связаны формулами закона Ома. Разновидностью делителя является потенциометр — переменное сопротивление, позволяющее плавно менять распределение напряжений.

В том, что делитель действительно делит подведенное к нему напряжение пропорционально сопротивлениям отдельных участков, легко убедиться, подключив вольтметр к каждому из резисторов.

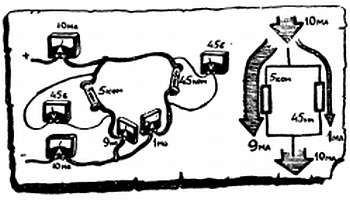
В переводе на русский «шунт» означает «обходной путь». Так называют резистор или другой элемент, подключаемый параллельно какому-либо участку цепи. Через шунт, естественно, идет часть тока, и, чем меньше шунтирующее сопротивление, тем больший ток ответвится в него, тем меньшая часть тока пойдет через шунтируемый участок цепи. Напряжение на резисторах, соединенных параллельно, всегда одинаково, а их общее сопротивление меньше наименьшего (Воспоминание № 6).

Если вы хотите убедиться в том, что усвоили понятия «делитель» и «шунт», попробуйте составить несколько эквивалентных схем (все детали представлены резисторами) уже знакомой нам цепи (рис. 41, листок А), состоящей из лампочек, выключателей и диодов. Составьте эквивалентные схемы этой цепи для всех возможных комбинаций включения и выключения Вк₁ и Вк₂, причем для обоих полупериодов. При этом считайте, что прямое сопротивление диода равно 2 ом, обратное — 20 ком и сопротивление лампочки — 200 ом.

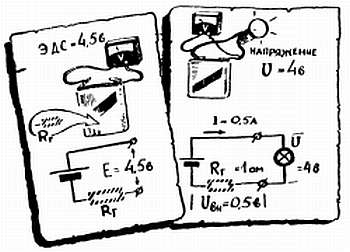
Пекарь, выпекающий хлеб, обязательно должен и сам чего-нибудь поесть. Так и генератор, вырабатывающий электрическую энергию, часть ее расходует на свои внутренние нужды. Можно сказать, что внутреннее сопротивление генератора R_г вместе с сопротивлением нагрузки R_н образует делитель (Воспоминание № 7): чем больше R_н по сравнению с R_г, тем большая часть э. д. с. достается нагрузке. Об этом можно сказать и иначе: чем меньше R_н, тем больше потребляемый от генератора ток, тем больше падение напряжения на R_г и, следовательно, меньше напряжение на выходе генератора.

Попробуйте постепенно увеличивать число лампочек, подключаемых параллельно батарейке карманного фонаря. Вы увидите, что, чем больше лампочек, тем более тускло горит каждая из них. Происходит это потому, что потребляемый ток растет, возрастают потери на внутреннем сопротивлении батареи и напряжение на ее зажимах падает. Естественно, что напряжение на выходе генератора зависит и от самого внутреннего сопротивления.

Пример. У старых батареек R_г сильно возрастает, и напряжение, которое дает такая батарея под нагрузкой, уменьшается. В то же время при отключенной нагрузке, когда ток через R_г практически не идет, вольтметр показывает у старых батарей нормальную э. д. с. (ток, потребляемый самим вольтметром, мал, и мы его не учитываем).

Все, о чем сейчас говорилось, относится к генератору в широком смысле слова. Генератором можно считать всякий элемент цепи, передающий энергию своему соседу независимо от того, как была получена эта энергия. Генератор — это и гальванический элемент, и антенна приемника, и транзисторный усилитель, и колебательный контур, и электрическая сеть. Во всех случаях нужно учитывать и то, что генератор отдает, и то, что теряется в нем самом; нужно учитывать и соотношение сопротивлений потребителя и самого генератора.

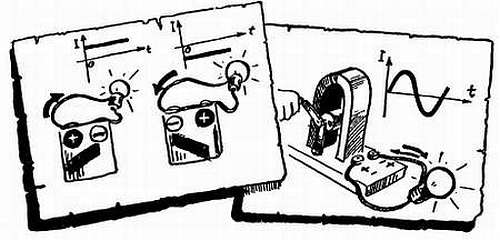
Генератор, на зажимах которого «плюс» и «минус» непрерывно меняются местами, дает переменное напряжение. А под действием переменного напряжения в цепи протекает переменный ток — заряды двигаются «туда» и «обратно». Для многих элементов (например, для лампочки, электроплитки, холодильника) совершенно безразлично, куда двигаются заряды, меняется ли их направление или остается неизменным. Главное — чтобы заряды двигались и работали. Но, конечно же, многие элементы электрических цепей совершенно по-разному ведут себя при постоянном и переменном токе. Более того, поведение многих элементов зависит от параметров (характеристик) переменного тока.

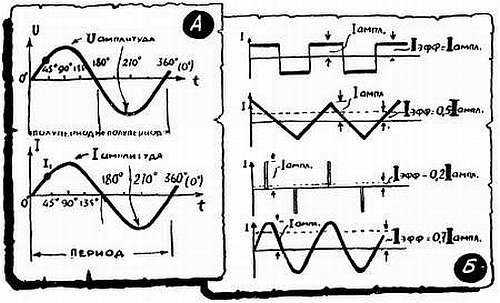
Период. Это время, в течение которого ток проходит полный цикл изменений. Измеряется в секундах. Иногда удобно вести речь о полупериодах, которые условно называют положительным и отрицательным.

Частота — число периодов в секунду. Измеряется в герцах (гц), килогерцах (кгц), мегагерцах (Мгц) и т. д. 1 гц = 1 период за 1 сек.

Амплитуда — наибольшее значение напряжения, тока или мощности. Измеряется соответственно в вольтах, амперах и ваттах. Напряжение и ток дважды за период достигают амплитудного значения — во время положительного и отрицательного полупериодов.

Мгновенное значение напряжения, тока, мощности. Посмотрев на часы и точно заметив момент времени, можно (по крайней мере, в мысленном опыте) измерить ток именно для этого момента. Это и будет мгновенное значение тока (напряжения, мощности). Естественно, для разных моментов времени мгновенные значения различны — на то у нас и переменный ток.

Форма кривой. Официально ее не числят в параметрах переменного тока. А зря. Судить о форме кривой, то есть о характере изменения тока (напряжения), можно по его графику. А точное описание формы переменного тока (напряжения) может дать спектр — набор синусоидальных составляющих (см. стр. 60).

Эффективное значение напряжения и тока. Амплитуда говорит о наибольшей работе, которую может выполнить переменный ток. Но ведь амплитудные значения бывают редко. Чтобы судить о работоспособности тока не в один какой-нибудь момент, а в течение длительного времени, вводится еще одна характеристика — эффективное значение тока. Оно указывает, какой величины нужно пустить в цепь постоянный ток, чтобы он работал так же, как и протекающий там переменный. Эффективное значение, как правило, меньше амплитуды, а вот на сколько меньше, это зависит уже от формы кривой, точнее, от того, каков переменный ток в интервалах между амплитудами. Для синусоидального переменного тока и напряжения (обратите внимание — только для синусоидального!) эффективный ток (напряжение) составляет 70 % амплитуды, или иначе — амплитуда на 30 % больше эффективного значения. Когда речь идет об электрических приборах или сети переменного напряжения, то приводят только эффективные токи и напряжения. Иными словами, в сети 220 в амплитуда достигает 310 в; в сети 127 в — около 180 в.

Фаза. Чтобы всякий раз не путаться с тысячными, сотыми или миллионными долями секунды, удобно разбить весь период, независимо от того, сколько он длится, на условные единицы времени — градусы. Весь период делят на 360°. При этом половина периода, естественно, равна 180°, четверть периода — 90° и т. д. Момент времени, соответствующий какому-нибудь определенному мгновенному значению тока (напряжения), называется фазой мгновенного значения. Так, например, на нашем графике А фаза положительной амплитуды — 90°, фаза отрицательной амплитуды — 270°, фазы нулевых значений — 0°, 180° и 360°, фаза помеченного на графике значения I₁ составляет 45°. Точно так же можно было бы отметить фазы и любого другого значения тока и напряжения. Ток и напряжение на этом графике изменяются синфазно — положительные и отрицательные амплитуды наступают у них в одни и те же моменты времени. Но так бывает не всегда.

Подключим к щей нагрузке два генератора. Их переменные напряжения могут действовать согласованно (в фазе), а могут действовать и не согласованно — со сдвигом фаз. В самом страшном случае генераторы просто работают друг против друга. Положительная амплитуда у одного из них появляется на позже, чем у другого, или, иными словами, напряжения сдвинуты по фазе на 180°. Возможны и другие сдвиги фаз между разными напряжениями, а кроме того, возможен сдвиг между переменным током и создавшим его переменным напряжением.

Чем быстрее меняется напряжение, тем больше ток через конденсатор, этим и объясняется уменьшение х_с с ростом частоты. Теперь посмотрите на график синусоидального напряжения: быстрей всего оно меняется, когда проходит через ноль, и именно в эти моменты в конденсаторе наблюдается амплитуда тока. Когда напряжение приближается к своей амплитуде, оно растет все медленнее, наконец как бы замирает на миг и начинает уменьшаться.

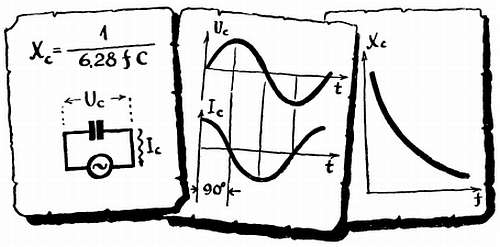
Вот именно во время этого «замирания» ток в цепи становится равным нулю, а затем меняет свое направление. Вывод: положительная амплитуда тока наступает на четверть периода раньше, чем положительная амплитуда напряжения, то есть ток через конденсатор опережает напряжение на нем на 90°.

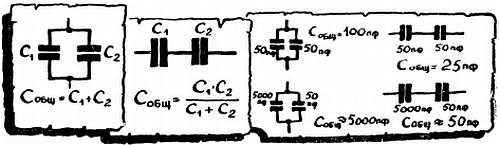
При параллельном соединении общая емкость конденсаторов равна сумме емкостей, при последовательном соединении общая емкость меньше наименьшей. Формулы для расчета общей емкости — это те же формулы для подсчета общего сопротивления (Воспоминания №№ 5 и 6), только «перепутанные»: формула для параллельного соединения R похожа на формулу для последовательного соединения С, а формула для последовательного соединения R — на формулу параллельного соединения С.

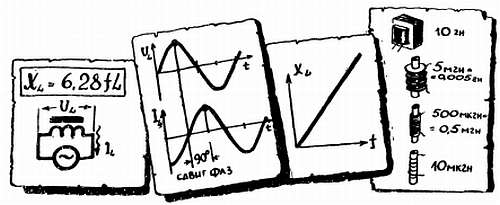
Когда изменяется ток в катушке, то изменяется созданное этим током магнитное поле, и в результате электромагнитной индукции (наведения) катушка сама в себе наводит электродвижущую силу. Величина этой э. д. с. самоиндукции зависит от скорости изменения тока (а значит, от его частоты), а также от некоторых свойств самой катушки, которые отображены в ее коэффициенте самоиндукции, или, иначе, индуктивности L. Индуктивность L, в частности, тем больше, чем больше витков. Резко увеличивает L сердечник из стали или другого ферромагнитного материала.

Единица индуктивности — генри (гн). Такой индуктивностью обладает катушка, в которой при изменении тока на 1 а за 1 сек наводится э. д. с. 1 в.

Электродвижущая сила самоиндукции всегда препятствует изменению тока: когда ток нарастает, она мешает ему нарастать, когда ток убывает, э. д. с. самоиндукции, наоборот, поддерживает его, затягивает процесс уменьшения тока. Этим самым катушка оказывает переменному току определенное сопротивление. Это так называемое индуктивное сопротивление x_L возрастает с увеличением частоты f (скорости изменения тока) и с ростом самой индуктивности L катушки. Напряжение на катушке и ток через нее также сдвинуты по фазе на 90°, но, в отличие от конденсатора, ток отстает от напряжения.

Индуктивность катушки, правда, очень приближенно можно определить по ее внешнему виду.

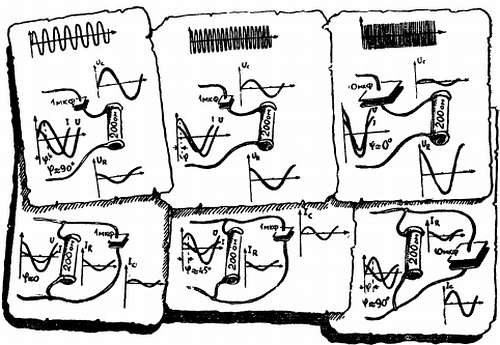
Когда в общую цепь одновременно включены и активные элементы (например, резисторы), и реактивные (например, конденсаторы), то в цепи могут возникать самые разные сдвиги фаз между общим током и общим напряжением — от 0 до 90°. Так, например, если конденсатор и резистор соединены последовательно, то через них идет один и тот же ток I. При этом напряжение U_R на резисторе совпадает по фазе с током, а напряжение на конденсаторе U_с, как обычно, отстает от него на 90°. Общее напряжение U на RС-цепочке отстает от тока тем сильнее, чем больше х_с по сравнению с R. А поскольку эти напряжения пропорциональны сопротивлениям х_с и R, то можно сказать, что сдвиг фаз определяется соотношением этих сопротивлений.

В отличие от последовательного соединения резисторов, общее сопротивление z определяется не как алгебраическая сумма (z не равно R + x_c), а как геометрическая сумма z = √(R² + x²_c). При последовательном соединении R и С влияние конденсатора возрастает с уменьшением частоты f и его емкости.

При параллельном соединении R и С на обоих этих элементах действует общее напряжение U, ток I_R совпадает с ним по фазе, ток I_c опережает на 90°. Чем больше ток I_c через конденсатор, тем сильнее результирующий сдвиг фаз между U и I. Иными словами, при параллельном соединении R и С влияние конденсатора тем сильнее, чем больше его емкость и чем выше частота.

Аналогично определяется сдвиг фаз и для цепей, содержащих индуктивность L. Но здесь с увеличением частоты и индуктивности влияние катушки при параллельном соединении уменьшается, а при последовательном — растет.

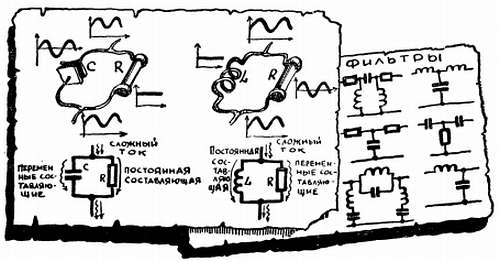
Цепи, состоящие из R и С, или R и L, или из всех трех элементов, находят чрезвычайно широкое применение в электронной аппаратуре. Они представляют собой фильтры, которые, обладая разным сопротивлением на разных частотах, позволяют отделить одни составляющие сложного тока от других.

Самый простой и самый популярный — это RС-фильтр. Через его емкостную ветвь, то есть через конденсатор, постоянный ток вообще не проходит, и RС-фильтр используется везде, где нужно отделить переменную составляющую от постоянной. Конденсатор пропускает переменный ток тем лучше, чем выше его частота. Подбором R и С можно добиться того, что на какой-то определенной частоте (а значит, и на более высоких частотах) большая часть тока — скажем, 90 % и более — будет замыкаться через С и лишь 10 % через R.

Аналогично по-разному пропускает разные частоты и RL-фильтр. Существует множество более сложных фильтров, которые осуществляют более «строгое» разделение переменных токов разных частот.

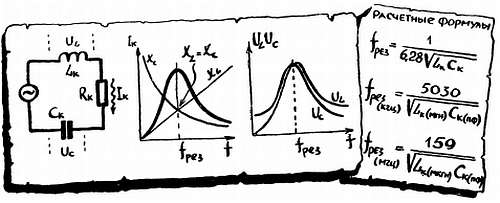
Очень интересно ведет себя при изменении частоты цепь, в которую входят и конденсатор С, и катушка L. Напряжения на этих элементах противофазны, так как ток в цепи общий. При этом U_c отстает от тока на 90°, a U_L опережает его, и тоже на 90°. Поэтому можно считать, что сопротивления х_с и x_L действуют друг против друга и общее реактивное сопротивление равно их разности.

На какой-то частоте — назовем ее резонансной f_рез — емкостное и индуктивное сопротивления окажутся равными. Они скомпенсируют друг друга, в цепи останется только активное сопротивление R_к. Из-за такого резкого уменьшения сопротивления резко возрастет ток, а вместе с ним возрастут напряжения на катушке и на конденсаторе.

Из условия х_с = x_L легко вычислить резонансную частоту f_рез. При отходе от резонансной частоты ток в цепи падает, так как общее сопротивление z растет (при увеличении частоты — за счет роста x_L, а при уменьшении частоты — за счет роста х_с). График, показывающий, насколько резко уменьшаются ток в цепи и напряжение на L и С при отходе от резонансной частоты, называется резонансной кривой. На резонансной частоте «с точки зрения» генератора сопротивление последовательного контура равно R_к (обычно единицы ом), а параллельного контура — R_экв (обычно десятки килоом).

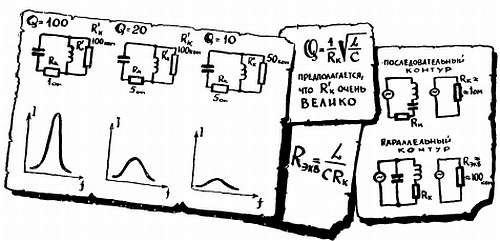
Увеличение тока при резонансе будет тем более резким, чем меньше активное сопротивление в сравнении с реактивным сопротивлением x_L и х_с. Величина, показывающая отношение x_L/R_к или (или x_с/R_к) называется добротностью Q. Добротность иногда называют множителем вольтажа, так как она показывает, во сколько раз напряжение на катушке и на конденсаторе во время резонанса превышает напряжение на активном сопротивлении. Из отношения x_L/R_к — легко вывести, что добротность тем выше, чем больше соотношение L/C. Увеличение R_к всегда приводит к ухудшению добротности, а значит, к снижению резонансного тока, а также напряжения на катушке и конденсаторе и к притуплению резонансной кривой. Ухудшить добротность можно еще и иначе: подключив параллельно конденсатору (катушке) шунтирующее сопротивление. В данном случае все наоборот: чем меньше это шунтирующее сопротивление, тем сильнее «задавлен» контур, тем хуже его добротность.

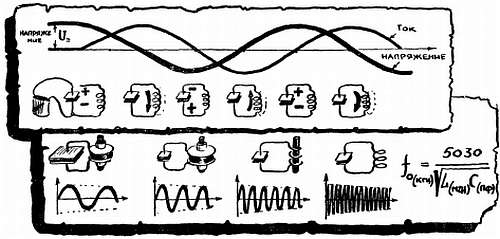
Явление резонанса, и, конечно, само название «резонанс», станет более понятным, если вспомнить, что цепь из конденсатора и катушки называется колебательным контуром, что в таком контуре возникают собственные электромагнитные колебания всякий раз, когда мы передаем в него некоторое количество энергии (например, заряжаем конденсатор).

«Возникают колебания» означает, что конденсатор непрерывно обменивается энергией с катушкой — энергия электрического поля периодически переходит в энергию магнитного поля. Затем происходит обратный переход, и все повторяется сначала. При этом в цепи протекает переменный ток, частота которого зависит от индуктивности L и емкости С, подобно тому как частота собственных колебаний струны зависит от ее массы и натяжения.

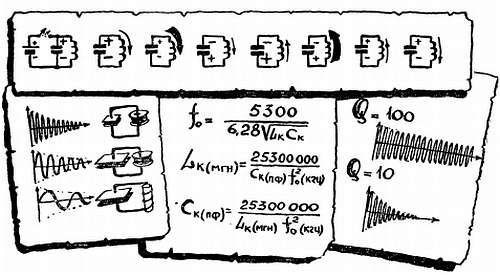
Частота собственных колебаний f₀ контура равна его резонансной частоте f_рез, и в этом заключен глубокий смысл. Резонанс наступает именно тогда, когда контур резонирует на частоту генератора, когда генератор действует в такт с собственными колебаниями в контуре.

Собственные колебания в контуре, если их не поддерживать, постепенно затухают, причем тем быстрее, чем больше потери энергии, чем ниже добротность Q контура.

Изменяя индуктивность и емкость контура, можно довольно просто менять частоту собственных колебаний и таким образом настраивать контур в резонанс на разные частоты. Так осуществляется настройка приемника на разные станции: переключением катушек переходят с одного диапазона на другой, а плавным изменением емкости производят настройку в пределах диапазона.

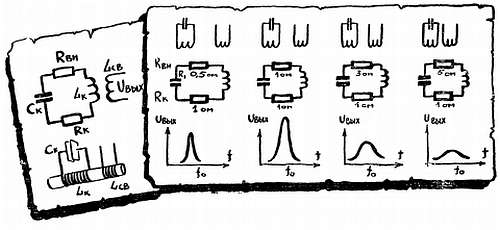
С помощью вспомогательной катушки связи L_св можно отобрать из контура часть энергии и передать «для дальнейшего прохождения службы». На первый взгляд кажется, что чем ближе сдвинуты катушки L_к и L_св, чем сильнее они связаны общим магнитным полем, тем больше энергии мы получим от контура, тем больно будет напряжение U_выx. В действительности же усиление связи между L_к и L_св может дать и обратный эффект: после некоторого «рубежа» дальнейшее сближение катушек приводит к уменьшению U_выx. Это связано с тем, что, отбирая у контура энергию, мы как бы вносим в него сопротивление R_вн.

Пока связь не очень сильная, это вносимое сопротивление играет второстепенную роль. Но по мере усиления связи роль эта становится все более значительной. Наконец дело доходит до того, что, сближая катушки, мы больше проигрываем от увеличения R_вн, чем выигрываем от увеличения доли получаемой из контура энергии.

При усилении связи во всех случаях ухудшается добротность контура и притупляется его резонансная кривая. Кроме того, несколько изменяется частота собственных колебаний f₀ (а значит, и резонансная частота), так как отбор энергии приводит к некоторому дополнительному сдвигу фаз между контурным током и напряжением. А это равносильно внесению в контур дополнительной емкости или индуктивности.

Главное, что нужно помнить, углубляясь в Воспоминания, — это то, что их нужно хоть когда-нибудь закончить. Сейчас, по-видимому, и для нас настало время закончить путешествие по прекрасному прошлому и двинуться в не менее прекрасное будущее. А это будущее прежде всего предстанет перед нами в виде самого сложного и в то же время, пожалуй, самого важного этапа на пути к транзисторным схемам. Нам предстоит научиться строить и анализировать входные и выходные характеристики транзистора. И тот, кто преодолеет этот участок пути (пусть даже не сразу), может смело считать, что главные трудности (и главные неприятности!) нашего путешествия уже позади.