Уникальные твиты

ОТВЕТ: Длина твита составляет 140 символов. В английском алфавите 26 букв – то есть 27 символов, если считать пробел. Используя эти знаки, можно составить 27¹⁴⁰ ~ 10²⁰⁰ возможных последовательностей.

Но «Твиттер» не ограничивается этими знаками. Можно поиграть с полным набором Unicode, где имеется более миллиона символов. «Твиттер» довольно сложно считает символы Unicode, но сумма возможных последовательностей может достичь 10⁸⁰⁰.

Конечно, почти все они будут бессмысленным набором букв и знаков из десятка разных языков. Даже если ограничиться латинским алфавитом, в получившихся последовательностях будут бессмыслицы вроде ptikobj. Но вопрос Эрика был о твитах, которые действительно несут какую-то информацию на английском языке. Сколько их может быть?

Это сложный вопрос. Первый порыв – позволить использовать только английские слова. Затем можно ограничить себя только грамматически правильными предложениями.

Но все равно возникают трудности. Например, Hi, I’m Mxyztplk – грамматически правильное предложение, если вас на самом деле так зовут. (Строго говоря, если подумать, оно грамматически правильное, даже если вы соврали.) Очевидно, не имеет смысла считать каждую фразу, начинающуюся со слов «Привет, я – …», отдельным предложением. Для англоязычного читателя Hi, I’m Mxyztplk практически неотличимо от Hi, I’m Mxzkqklt, и засчитывать оба не стоит. Зато Hi, I’m xPoKeFaNx, очевидно, отличается от первых двух, хотя xPoKeFaNx никак нельзя посчитать английским словом.

Итак, этот способ отбора, похоже, не работает.

К счастью, есть более удачный подход.

Давайте представим себе язык, в котором есть только два верных предложения, и каждый твит должен быть одним из этих предложений. Это:

и

Тогда лента вашего «Твиттера» выглядела бы вот так:

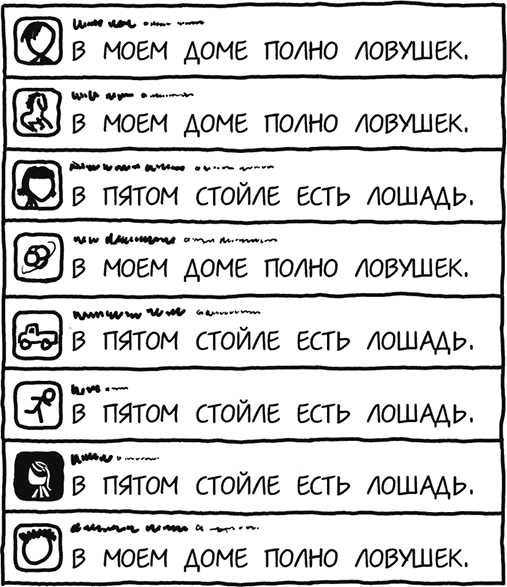
Эти сообщения довольно длинные, но в них не очень много информации – они только показывают, выбрал человек сообщение про ловушки или про лошадь. По сути, это двоичный код – цифра 0 или цифра 1. Хотя здесь много букв, для читателя, владеющего этим языком, каждый твит содержит лишь один бит информации.

Этот пример подводит нас к важной идее о том, что информация фундаментально связана с неуверенностью получателя в содержании сообщения и его неспособностью предсказать это содержание заранее.

Клод Шэннон – который практически в одиночку изобрел современную теорию информации – придумал хитрый метод, чтобы измерять информационную содержательность языка. Он показывал группам людей образцы типичного английского текста, которые были произвольно оборваны, и предлагал угадать, какая буква последует дальше.

Основываясь на частоте верных догадок – и сложном математическом анализе, – Шэннон определил, что информационная насыщенность типичного письменного английского составляет 1–1,2 бита на букву. Это значит, что хороший алгоритм сжатия должен позволять сжать английский текст в кодировке ASCII, в котором восемь бит на букву, примерно до одной трети изначального объема. И в самом деле, если применить к электронной книге в формате .txt хороший архиватор, примерно это и произойдет.

Если фрагмент текста содержит n бит информации, в определенном смысле это значит, что есть 2ⁿ сообщений, которые он может передавать. Конечно, не обошлось без математического жонглирования (в частности, в том, что касается длины сообщения и штуки под названием «расстояние единственности»), но суть в том, что предположительное количество различных осмысленных твитов на английском составляет 2^140×1,1 = 2 × 10⁴⁶, а не 10²⁰⁰ или 10⁸⁰⁰.

И сколько же времени потребуется миру, чтобы прочесть их все вслух?

Чтение 2 × 10⁴⁶ твитов займет у человека порядка 10⁴⁷ секунд.

Неважно, читает ли их один человек или миллиард, – этих твитов так много, что нельзя прочесть сколько-нибудь существенную их часть, даже если читать все то время, что существует Земля.

Давайте лучше вернемся к птичке, которая точит клюв о скалу. Предположим, что раз в тысячу лет птица откалывает от скалы маленький кусочек и, улетая, уносит на себе несколько десятков крупиц камня. (Нормальная птица оставила бы на скале вещества клюва, чем унесла бы камня, но в этой истории нет ничего нормального, так давайте просто продолжим в том же духе.)

Предположим, вы читаете твиты вслух по 16 часов в день, ежедневно. И за вашей спиной каждую тысячу лет прилетает птица и соскребает несколько невидимых крупиц с вершины скалы.

Когда скала будет сточена до основания, пройдет один день вечности.

Скала появляется снова, и цикл возобновляется еще на один день вечности. 365 дней вечности = каждый из них длиной 10³² лет – составляют год вечности.

Сотня лет вечности, за которые птица сточит 36 500 скал, составит столетие вечности.

Но столетия не хватит. Как и тысячелетия.

Чтобы прочесть все твиты, вам потребуется десять тысяч лет вечности.

Этого времени достаточно, чтобы увидеть, как разворачивается вся история человечества с момента изобретения письменности и до сего дня – если каждый день будет занимать столько времени, сколько нужно птичке, чтобы сточить скалу.

Кажется, что 140 знаков – это немного, но нам всегда будет что сказать.