В эпоху Ньютона было известно, что четыре тела Солнечной системы обладают спутниками: у Юпитера, Сатурна и Земли есть свои спутники, а все планеты в то же время сами являются спутниками Солнца. По Закону всемирного тяготения тело массой M оказывает воздействие силой F = GMm/r² на спутник массой m на расстоянии r (где G – мировая гравитационная постоянная), поэтому по Второму закону Ньютона центростремительное ускорение, которое испытывает этот спутник, вычисляется как a = F/m = GM/r². Значение константы G и общие размеры Солнечной системы еще не были известны во времена Ньютона, но эти неизвестные величины не фигурируют в выражениях для отношений масс, рассчитываемых исходя из отношений расстояний и отношений центростремительных ускорений. Если два спутника тел с массами M₁ и M₂ обнаруживаются на некоторых расстояниях r₁ и r₂ от своих центральных тел, для которых известно их отношение r₁/r₂, а также отношение их центростремительных ускорений a₁/a₂, то отношение масс двух тел можно найти по формуле:

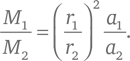
В частности, если спутник движется с постоянной скоростью v по круговой орбите радиусом r, его орбитальный период равен T = 2πr/v, поэтому его центростремительное ускорение v²/r равняется a = 4π²r/T², отношение ускорений двух спутников a₁/a₂ = (r₁/r₂)/(T₂/T₁) 2, а отношение масс, выведенное из орбитальных периодов и отношений расстояний, равно:

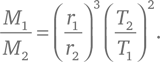
К 1687 г. все соотношения расстояний между планетами и Солнцем были хорошо известны, а зная по результатам наблюдений максимальные угловые расстояния между Юпитером и его спутником Каллисто, а также Сатурном и его спутником Титаном (который Ньютон называл «гюйгенсовым спутником»), можно было вывести отношения расстояния от Каллисто до Юпитера к расстоянию от Юпитера до Солнца, а также расстояния от Титана до Сатурна к расстоянию от Сатурна до Солнца. Расстояние от Луны до Земли было точно измерено в единицах земного диаметра, но не в отношении к расстоянию между Землей и Солнцем – тогда это значение еще не было известно. Ньютон использовал грубую прикидку для расстояний между Землей и Луной, а также между Землей и Солнцем, и использованные им значения несли значительную ошибку. Не считая этой конкретной проблемы, отношения скоростей и центростремительных ускорений планет и спутников хорошо выводились его методом из их известных орбитальных периодов обращения (на самом деле Ньютон взял для расчета период обращения Венеры, а не Юпитера или Сатурна, но это не повлияло на результат, поскольку соотношения расстояний от Солнца Венеры, Юпитера и Сатурна были достоверно известны). Как мы говорили в главе 14, полученные Ньютоном отношения масс Юпитера и Сатурна к массе Солнца были достаточно точны, тогда как рассчитанное им отношение массы Земли к массе Солнца было совершенно ошибочным.