Как мы видели в техническом замечании 22, тонкая выпуклая линза будет фокусировать лучи света, которые падают параллельно ее центральной оси, в точке F на этой оси, на расстоянии за линзой, которое называется фокусным расстоянием f для этой линзы. Параллельные лучи света, которые падают под небольшим углом γ к центральной оси, также будут фокусироваться этой линзой, но в точке, которая немного смещена от центральной оси. Чтобы увидеть, как далеко она сместится, мы можем мысленно повернуть путь луча на рис. 16а вокруг линзы на угол γ. Расстояние d от фокуса до центральной оси линзы составит тогда ту же долю длины окружности радиусом f, что и угол γ от 360°:

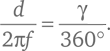
Следовательно,

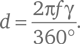
Это работает только для тонких линз; иначе d также зависит от угла θ, упомянутого в техническом замечании 22. Если лучи света от какого-либо далекого объекта падают на линзу под углами, попадающими в промежуток Δγ (дельта гамма), то они будут фокусироваться на вертикальном отрезке длиной Δd, значение которого можно выразить как:

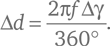
Как обычно, эта формула становится проще, если измерять Δγ в радианах, равных 360°/2π, а не в градусах. В таком случае она читается просто как Δd = f Δγ. Этот участок, где фокусируется свет, называется мнимым изображением (см. рис 17а).

Мы не можем увидеть мнимое изображение, просто посмотрев на него, потому что после того, как оно получается, лучи света снова рассеиваются. Чтобы сфокусироваться в точке на сетчатке расслабленного человеческого глаза, лучи света должны войти в него по более или менее параллельным направлениям. В телескопе Кеплера была вторая выпуклая линза, которую называют окуляром, чтобы фокусировать расходящиеся лучи света от мнимого изображения так, чтобы они параллельно выходили из телескопа. Повторив те же рассуждения для лучей света, идущих в противоположном направлении, мы увидим, что для того, чтобы лучи света, расходящиеся от точки, покидали телескоп по параллельным направлениям, окуляр должен находиться на расстоянии f′ от мнимого изображения, где f′ – это фокусное расстояние окуляра (см. рис. 17б). Это означает, что длина телескопа L должна составлять сумму фокусных расстояний:

Промежуток Δγ’ направлений лучей света, входящих в глаз от различных точек источника, связан с размером мнимого изображения по формуле:

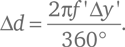
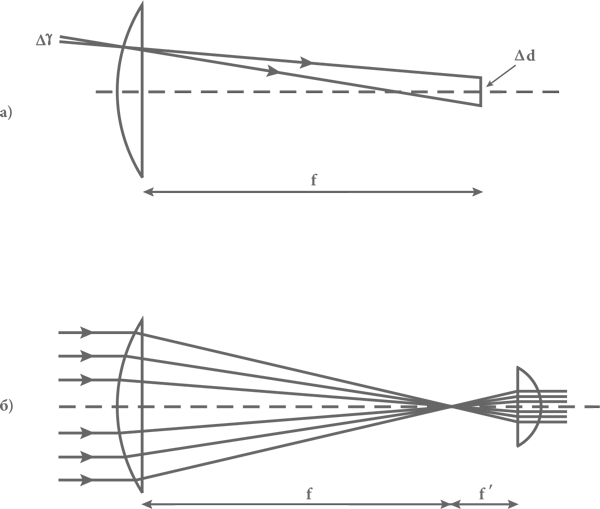
Рис. 17. Телескопы: а) формирование мнимого изображения. Две сплошные линии со стрелками обозначают лучи света, которые входят в линзу и разделены небольшим углом Δγ. Эти линии (и другие, параллельные им) фокусируются на расстоянии f от линзы на вертикальном отрезке длиной Δd, пропорциональной Δγ; б) линзы в телескопе системы Кеплера. Линии со стрелками обозначают путь лучей света, которые идут к слабой выпуклой линзе от далекого объекта по практически параллельным направлениям; фокусируются с помощью линзы в точке на расстоянии f от линзы; расходятся от этой точки и преломляются сильной выпуклой линзой, чтобы войти в глаз наблюдателя по параллельным направлениям.

Видимый размер объекта пропорционален углу, под которым видны противоположные стороны удаленного объекта, поэтому увеличение телескопа равно отношению угла, под которым лучи света от краев объекта, выходящие из окуляра, входят в глаз наблюдателя, к углу, под которым они входили бы, если бы телескопа не было:

Подставив в это соотношение две формулы, которые мы вывели для определения размера Δd мнимого изображения, мы увидим, что увеличение равно:

Чтобы получить значительное увеличение, нам нужно, чтобы линза в передней части телескопа была намного слабее окуляра, то есть f >>f′.

Это не так уж легко сделать. В соответствии с формулой фокусного расстояния, данной в техническом замечании 22, чтобы получить сильный стеклянный окуляр с коротким фокусным расстоянием f′, его линза должна иметь маленький радиус кривизны, что означает, что она либо должна быть очень маленькой, либо не должна быть тонкой (то есть толщина должна быть намного меньше радиуса кривизны). В обоих этих случаях окуляр не сможет хорошо фокусировать свет. Вместо этого мы можем взять слабую переднюю линзу с большим фокусным расстоянием f, но в таком случае длина телескопа L = f + f′ ≈ f должна быть очень большой. Галилею потребовалось некоторое время, чтобы внести в свой телескоп изменения, давшие ему достаточное увеличение для астрономических целей.

Галилео сделал свой телескоп немного другим – с вогнутым окуляром. Как уже упоминалось в техническом замечании 22, если разместить вогнутую линзу так, чтобы она сводила в одну точку входящие в нее лучи света, они будут выходить по параллельным направлениям. Фокусное расстояние – это расстояние позади линзы, на котором лучи света сходились бы в одной точке, если бы линзы не было. В телескопе Галилея была слабая выпуклая линза впереди с фокусным расстоянием f и сильная вогнутая линза с фокусным расстоянием f′ позади нее, перед тем местом, где должно было находиться мнимое изображение, если бы вогнутой линзы не было. Увеличение этого телескопа, опять же, составляет f/f ′, но его длина равна только f − f′ вместо f + f′.