Книга: Объясняя мир. Истоки современной науки
Назад: 20. Суточный параллакс
Дальше: 22. Фокусное расстояние линзы
21. Правило равных площадей и эквант
Согласно Первому закону Кеплера, все планеты, включая Землю, обращаются вокруг Солнца по эллиптическим орбитам, причем Солнце находится не в их центрах, а в некоторых смещенных от центра точках, расположенных на больших осях этих эллипсов – в одном из фокусов эллипса каждой из орбит (см. техническое замечание 18). Эксцентриситет эллипса e определяется так, что расстояние от любого его фокуса до центра равно ea, где a – длина большой полуоси эллипса. Также, согласно Второму закону Кеплера, скорость каждой планеты при ее перемещении по орбите не постоянна, а изменяется таким образом, что отрезок (или радиус-вектор), проведенный к ней от Солнца, заметает равные по площади участки плоскости за одинаковые отрезки времени.
Существует другой способ приближенно сформулировать тот же Второй закон, имеющий близкое отношение к старой идее экванта, которую использовал в своей астрономической системе Птолемей. Вместо того чтобы рассматривать отрезок, проведенный к планете от Солнца, рассмотрим отрезок к ней же из другой точки, а именно из пустого фокуса ее эллиптической орбиты. Эксцентриситет e некоторых орбит планет довольно значителен, и им нельзя пренебрегать. Но его квадрат e² очень мал для любой планеты. Например, среди планет самый большой эксцентриситет у орбиты Меркурия, для него e = 0,206, а e² = 0,042; для Земли же e² = 0,00028. Поэтому при вычислении планетных движений достаточно аппроксимировать реальные их законы уравнениями, в которых присутствуют слагаемые, пропорциональные эксцентриситету e, или независимые от него слагаемые, и игнорировать такие их члены, которые пропорциональны квадрату эксцентриситета e² или его степеням высших порядков. В этом приближении Второй закон Кеплера эквивалентен утверждению, что отрезок, проводимый из пустого фокуса планетной орбиты к планете, заметает равные углы за равные промежутки времени. Иначе говоря, эта линия вращается с постоянной угловой скоростью.
На конкретном примере покажем, что если 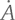 – это скорость, с которой радиус-вектор от Солнца к планете заметает равные площади, а
– это скорость, с которой радиус-вектор от Солнца к планете заметает равные площади, а  (фи с точкой) – скорость изменения угла между радиус-вектором от пустого фокуса к той же планете и большой осью ее орбиты, то верно равенство
(фи с точкой) – скорость изменения угла между радиус-вектором от пустого фокуса к той же планете и большой осью ее орбиты, то верно равенство
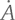 – это скорость, с которой радиус-вектор от Солнца к планете заметает равные площади, а
– это скорость, с которой радиус-вектор от Солнца к планете заметает равные площади, а  (фи с точкой) – скорость изменения угла между радиус-вектором от пустого фокуса к той же планете и большой осью ее орбиты, то верно равенство
(фи с точкой) – скорость изменения угла между радиус-вектором от пустого фокуса к той же планете и большой осью ее орбиты, то верно равенство

где O (e²) – обозначение всех членов, пропорциональных e² или степеням e еще более высоких порядков, а R – коэффициент, значение которого зависит от применяемых единиц измерения углов. Если мы меряем углы в градусах, то R = 360°/2π = 57,293…°, то есть угол размером в один радиан. Или мы можем измерять углы в радианах, и тогда R = 1. Второй закон Кеплера гласит, что за одинаковые промежутки времени площадь, заметаемая радиус-вектором планеты, одна и та же. Это значит, что 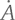 – величина постоянная, а, следовательно, что постоянна и с точностью до слагаемых высшего порядка, пропорциональных e². Поэтому с достаточной точностью можно сказать, что за заданный промежуток времени угол, на который изменяется радиус-вектор планеты из пустого фокуса ее орбиты, всегда один и тот же.
– величина постоянная, а, следовательно, что постоянна и с точностью до слагаемых высшего порядка, пропорциональных e². Поэтому с достаточной точностью можно сказать, что за заданный промежуток времени угол, на который изменяется радиус-вектор планеты из пустого фокуса ее орбиты, всегда один и тот же.
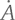 – величина постоянная, а, следовательно, что постоянна и с точностью до слагаемых высшего порядка, пропорциональных e². Поэтому с достаточной точностью можно сказать, что за заданный промежуток времени угол, на который изменяется радиус-вектор планеты из пустого фокуса ее орбиты, всегда один и тот же.
– величина постоянная, а, следовательно, что постоянна и с точностью до слагаемых высшего порядка, пропорциональных e². Поэтому с достаточной точностью можно сказать, что за заданный промежуток времени угол, на который изменяется радиус-вектор планеты из пустого фокуса ее орбиты, всегда один и тот же.Что касается описанной Птолемеем теории, центр эпицикла каждой планеты обращается вокруг Земли по круговой орбите, деференту, но Земля находится не в центре деферента. Орбита является эксцентричной, то есть Земля находится в точке, отделенной от центра деферента небольшим расстоянием. Мало того, скорость, с которой центр эпицикла обращается вокруг Земли, не постоянна, и угловая скорость, с которой луч от Земли к этому центру поворачивается, тоже не постоянна. Чтобы детально учесть все особенности наблюдаемого движения планет, Птолемей изобрел понятие экванта. Это точка по другую сторону от центра деферента по отношению к Земле, которая находится на том же расстоянии от центра, что и Земля. Луч, проводимый к центру эпицикла от этого экванта (а не от Земли), и должен был описывать равные углы в одни и те же промежутки времени.
Внимательный читатель уже заметил, что это очень похоже на картину, описываемую законами Кеплера. Конечно, роли Солнца и Земли в астрономических системах мира Птолемея и Коперника противоположны, но пустой фокус эллипса в теории Кеплера играет ту же самую роль, что и эквант в теории Птолемея, а Второй закон Кеплера объясняет, почему введение экванта помогло улучшить теоретические предсказания видимых положений планет по теории Птолемея.
Теперь докажем равенство (1). Определим θ как угол между большой осью эллипса и отрезком, соединяющим Солнце и планету, и вспомним, что φ определен как угол между той же большой осью и отрезком, соединяющим планету и пустой фокус. Так же, как в техническом замечании 18, обозначим длины этих отрезков r+ и r– то есть расстояния от Солнца до планеты и от планеты до пустого фокуса орбиты соответственно. Как было показано, они равны

где х – горизонтальная координата точки на эллипсе, то есть расстояние между точкой и прямой, секущей эллипс вдоль его малой оси.
Косинус угла определяется в тригонометрии с использованием прямоугольного треугольника, один из углов которого равен данному: косинусом называется отношение длины катета, прилежащего к этому углу, к длине гипотенузы треугольника. Поэтому из рис. 15 мы можем записать:
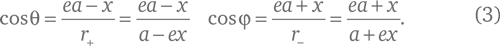
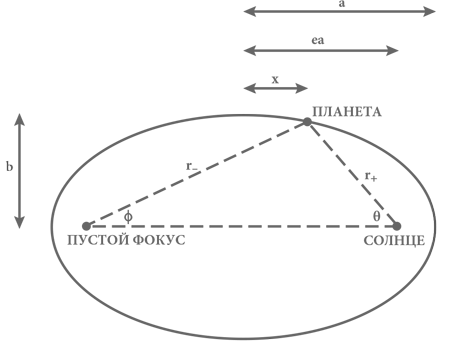
Рис. 15. Орбитальное движение планеты по эллипсу. Орбита планеты вычерчена здесь как эллипс, имеющий эксцентриситет (как и на рис. 12) около 0,8 – значительно больше, чем у какой-либо планеты Солнечной системы. Отрезки, обозначенные r+ и r−, соединяют планету, соответственно, с Солнцем и с противоположным ему, пустым фокусом эллипса.
Уравнение слева мы можем решить, найдя из него x:

Подставляя результат в формулу для cos φ, выражаем связь между углами θ и φ:
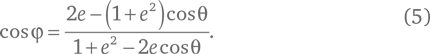
Поскольку равенство справедливо при любых значениях угла θ, изменение в левой части равенства должно быть равно изменению в правой части при любом изменении θ. Допустим, мы производим бесконечно малое его изменение δθ (дельта тета). Чтобы рассчитать, насколько изменится φ, прибегнем к правилу дифференциального исчисления, согласно которому изменение любого угла α (это может быть θ или φ) на величину δα (дельта альфа) приводит к изменению cos α на величину – (δα/R) sin α. Оттуда же при изменении любой функции f, такой, например, как знаменатель в уравнении (5), на ничтожно малую величину δf изменение в отношении 1/f составляет −δf/f2. Приравняв соответствующие изменения с обеих сторон равенства, получаем:
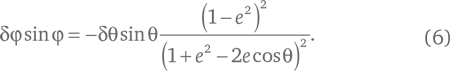
Теперь нам нужна формула, связывающая sin φ и sin θ. Для этого посмотрим на рис. 15 и обратим внимание, что вертикальная координата y точки на линии эллипса выражается как y = r + sin θ, а также y = r − sin φ, и, поделив их, сократив y, получаем:
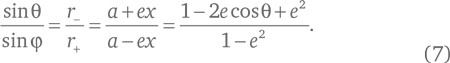
Совмещая уравнения (7) и (6), имеем:

Итак, какова же площадь, описываемая радиус-вектором планеты, проведенным от Солнца, когда угол θ изменяется на δθ? Измеряя углы в градусах, мы можем сказать, что это площадь равнобедренного треугольника, две равные стороны которого имеют длину r+, а третья – маленькая часть дуги общей длиной 2πr+ окружности радиусом r+, равная 2πr+ × δθ/360°. Она равна
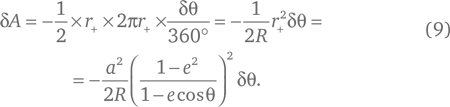
В этой формуле поставлен минус, поскольку мы хотим, чтобы величина δA росла, если увеличивается угол φ; но если вспомнить, как мы определили эти углы, φ будет расти в том случае, если уменьшается θ, поэтому δφ больше нуля, когда δθ меньше нуля. Поэтому уравнение (8) можно переписать в виде:
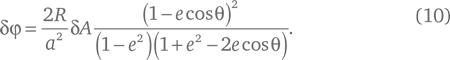
Принимая, что δA и δφ – описываемая первым радиус-вектором площадь и угол поворота второго радиус-вектора за ничтожно малый промежуток времени δt, и поделив обе части уравнения (10) на δt, найдем соответствие между описываемыми площадями и углами в виде равенства
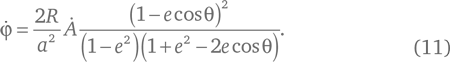
Нами получено точное равенство. Но теперь посмотрим, как оно себя ведет в том случае, когда e очень мал. Числитель второй дроби в уравнении (11) имеет вид (1 − e cos θ)² = 1 − 2e cos θ + e²cos²θ, так что слагаемые нулевого и первого порядка в числителе и знаменателе дроби одни и те же, и вся разница между числителем и знаменателем заключается в коэффициентах членов, пропорциональных e². И значит, уравнение (11) полностью соответствует искомому нами с самого начала равенству (1). Для большей определенности мы можем оставить в уравнении (11) члены порядка e²:
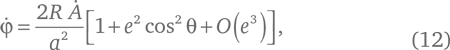
где O (e³) обозначает члены, пропорциональные e³ или более высоким степеням e.
Назад: 20. Суточный параллакс
Дальше: 22. Фокусное расстояние линзы

