Аристарх использовал четыре наблюдательных факта, чтобы определить расстояния от Земли до Солнца и Луны, а также диаметры Солнца и Луны. Все полученные результаты он выразил в единицах диаметра Земли. Рассмотрим каждое из выполненных им наблюдений по очереди и посмотрим, что можно узнать, основываясь на них. Далее расстояния между Землей и Солнцем и Землей и Луной будут обозначаться соответственно dс и dл, а диаметры Солнца, Луны и Земли – Dс, Dл и Dз. Предполагая, что диаметры этих тел ничтожно малы по сравнению с расстояниями между ними, примем, что в рассуждениях о расстояниях между Землей, Луной и Солнцем не обязательно брать во внимание расположение на Земле точек, из которых выполняются наблюдения.

Если в этот момент смотреть с Луны, угол между направлениями на Солнце и на Землю должен составлять точно 90° (см. рис. 5а), поэтому треугольник, образованный отрезками Луна – Солнце, Луна – Земля и Земля – Солнце, является прямоугольным, в котором отрезок Земля – Солнце есть гипотенуза. Отношение катета, прилежащего к углу θ (тета) в прямоугольном треугольнике, к его гипотенузе – тригонометрическая функция косинус угла θ, которая обозначается cos θ, и ее значение мы можем взять из таблицы или рассчитать на калькуляторе с тригонометрическими функциями. Итак,

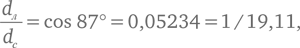
и значит, из наблюдения следует, что Солнце в 19,11 раз дальше от Земли, чем Луна. Не зная тригонометрии, Аристарх мог лишь заключить, что это число не меньше 19 и не больше 20. На самом деле этот угол равен не 87°, а 89,853°, и поэтому Солнце в действительности находится в 389,77 раз дальше от Земли, чем Луна.

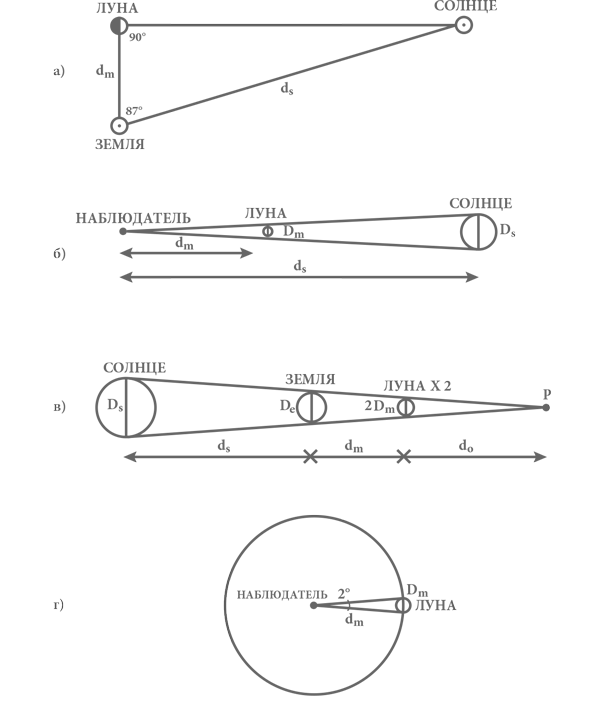
Рис. 5. Четыре наблюдения, которые Аристарх использовал для расчета размеров Солнца и Луны и расстояний от Земли до них: а) треугольник, образуемый Землей, Солнцем и Луной в момент, когда Луна находится в середине фазы первой или последней четверти; б) диск Луны точно закрывает диск Солнца для земного наблюдателя во время полного солнечного затмения; в) Луна заходит в тень Земли во время полного лунного затмения. Сфера, которая на месте Луны точно перекрывала бы конус тени, имеет диаметр, вдвое больший, чем у Луны, а точка P – крайняя точка конуса тени, отбрасываемой Землей; г) видимый угловой размер Луны по Аристарху составляет 2°; истинное его значение близко к 0,5°.

Это показывает, что у Луны и Солнца примерно один и тот же видимый угловой размер, в том смысле, что угол между направлениями от земного наблюдателя на противоположные края диска Солнца такой же, как между направлениями на противоположные края диска Луны (см. рис. 5б). Отсюда следует, что треугольники, образуемые этими линиями и поперечными диаметрами Луны и Солнца, являются «подобными», то есть углы при вершинах у них попарно равны. Поскольку соотношения размеров сторон в подобных треугольниках одинаковы для всех сторон, то

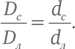
Исходя из результатов наблюдения 1, Аристарх получил значение отношения D_с/D_л = 19,11, в то время как настоящее соотношение диаметров двух тел близко к 390.

Обозначим P точку, где находится вершина конуса тени, отбрасываемой Землей. У нас получается три подобных треугольника: треугольник, образованный поперечным диаметром Солнца и линиями между его концами и точкой P; треугольник, образованный поперечным диаметром Земли и линиями между его концами и точкой P; и треугольник, образованный двойным поперечным диаметром Луны и линиями между его концами и точкой P (см. рис. 5в). Следовательно, соотношения подобных сторон во всех этих треугольниках взаимно равны. Предположим, что точка P находится на расстоянии d₀ позади Луны. Тогда расстояние между этой точкой и Солнцем составляет d_с + + d_л + d₀, а между ней же и Землей – d_л + d₀, поэтому

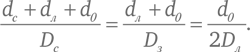
Выполнив несложные алгебраические преобразования, мы можем найти из второго равенства выражение для d₀:

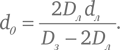
Подставляя его в первое равенство и перемножая обе части на D_зD_с (D_з – 2D_л), получаем:

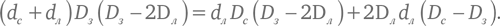
Слагаемые d_лD_с × (−2D_л) в левой части и 2D_лd_лD_с в правой части взаимно обращаются в 0. Оставшиеся в правой части слагаемые имеют общий множитель D_з, который сокращается с множителем D_з в левой части. Таким образом, у нас получается формула для D_з:

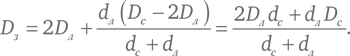
Зная результат наблюдения 2, то есть выведенное нами равенство d_с/d_л = D_с/D_л, уравнение выше может быть записано с использованием одних лишь диаметров небесных тел:

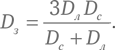
Если мы используем полученное ранее численное значение D_с/D_л = 19,1, это даст D_з/D_л = 2,85. Аристарх выразил значение этого отношения как лежащее между 108/43 = 2,51 и 60/19 = 3,16, и число 2,85 замечательно попадает в этот промежуток. Но его настоящее значение равно 3,67. Причина того, что результат Аристарха оказался довольно близок к истинной величине, несмотря на сильную ошибку в оценке отношения D_с/D_л, в том, что результат вычисления малочувствителен к точному значению D_с, если D_с много больше D_л. В самом деле, если мы совсем выкинем из знаменателя слагаемое D_л как ничтожно малое по сравнению с D_с, то D_с в числителе и знаменателе сократятся, и у нас получится просто D_з = 3D_л, что не так уж далеко от истины.

Но значительно более важное историческое значение имел тот факт, что, совмещая значения отношений D_с/D_л = 19,1 и D_з/D_л = 2,85, легко найти, что D_с/D_з = 19,1/2,85 = 6,70. И хотя по-настоящему D_с/D_з = 109,1, уже и такой результат показывал, что Солнце значительно больше Земли. Аристарх усилил эффект, показав сравнение соотношения не диаметров, а объемов двух тел: если соотношение их диаметров равно 6,7, то соотношение их объемов будет равняться 6,73 = 301. Именно это сопоставление, если верить Архимеду, привело Аристарха к мысли, что Земля обращается вокруг Солнца, а не Солнце вокруг Земли.

Уже описанные нами выкладки Аристарха дают значения всех соотношений диаметров Солнца, Луны и Земли, а также значение отношения расстояний до Солнца и Луны. Однако пока мы никак не можем связать соотношением какой-либо диаметр тела с расстоянием между телами. Это становится возможно при учете результата четвертого наблюдения:

Поскольку угловой размер дуги полной окружности равен 360° (см. рис. 5 г) и длина окружности радиусом dл равна 2πdл, то диаметр Луны равен

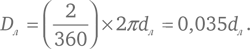
По Аристарху, значение отношения D_л/d_л лежит в промежутке между 2/45 = 0,044 и 1/30 = 0,033. По неизвестным причинам в сохранившихся трудах Аристарх грубо ошибается в своей оценке видимого углового диаметра Луны. На самом деле он составляет 0,519°, что сводит значение D_л/d_л к 0,0090. Как мы отметили в главе 8, Архимед в своем труде «Исчисление песчинок» дает величину для углового диаметра Луны 0,5°, что довольно близко к истинному значению и могло бы дать правильные оценки диаметра Луны и расстояния до нее.

Используя результаты наблюдений 2 и 3, из которых Аристарх получил отношение D_з/D_л диаметров Земли и Луны, и свой результат наблюдения 4, давший ему отношение D_л/d_л диаметра Луны к расстоянию до нее, он смог найти отношение расстояния до Луны к диаметру Земли. Например, полагая D_з/D_л = 2,85 и D_л/d_л = 0,035, получаем:

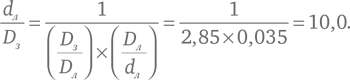
(Истинное значение – около 30.) Далее, совмещая эту величину с результатом наблюдения 1, дающим отношение расстояния от Земли до Солнца и до Луны как d_с/d_л = 19,1, Аристарх нашел, что расстояние от Земли до Солнца в d_с/D_з = 19,1 × 10,0 = 191 раз больше диаметра Земли, тогда как в действительности оно в 11 600 раз больше. Осталось измерить Землю, но это уже следующая задача.