Настоящая научная работа с данными

Книга: Много цифр. Анализ больших данных при помощи Excel

Итак, вы научились работать с переменными и типами данных, вбивать данные вручную и читать их из файлов CSV. Но как на самом деле используются алгоритмы, рассмотренные в этой книге? Поскольку у вас уже есть загруженные данные о вине, начнем с небольшой кластеризации по k-средним.

Сферическое k-среднее винных данных в нескольких линиях

В этом разделе мы проведем кластеризацию на основе близости косинусов (которая также называется сферическим k-средним). Скачайте и загрузите в R пакет сферического k-среднего под названием skmeans. Для справки; skmeans не является частью R, он написан сторонними специалистами. Эти гении сделали всю работу за вас, а вам осталось только с благодарностью пользоваться плодами их трудов.

Как и большинство пакетов для R, этот пакет вы можете установить (почитав об этом, если требуется) из Comprehensive RArchive Network (CRAN). CRAN – это хранилище многих полезных пакетов для расширения функциональности R. Их список находится здесь: .

Вбейте в поиск rseek.org «shperical k-means». Первым «выскочит» PDF, описывающий этот пакет. Функция, которую вы ищете, называется skmeans().

R изначально настроена на загрузку пакетов с CRAN, так что для загрузки skmeans можно использовать функцию R install.packages() (R может попросить установить персональную библиотеку при первом запуске):

> install.packages(«skmeans»,dependencies = TRUE)

trying URL 1 http://mirrors.nics.utk.edu/cran/bin/macosx/leopard/

contrib/2.15/skmeans_0.2–3.tgz'

Content type 1application/x-gzip' length 224708 bytes (219 Kb) opened URL

downloaded 219 Kb

Видите, как в коде я установил значение dependencies=TRUE в запросе на установку. Теперь я уверен в том, что если пакет skmeans зависит от каких-либо других пакетов, R загрузит и их тоже. По запросу соответствующий моей версии R пакет (у меня 2.15 для MacOS) загружается с зеркала сайта и инсталлируется в положенное место.

Сам пакет можно загрузить с помощью функции library():

library(skmeans)

Чтобы узнать, как пользоваться skmeans(), наберите перед названием функции? Документация определяет свойство skmeans() принимать матрицы, в которых каждый столбец соотнесен с объектом или кластером.

Ваши данные ориентированы по столбцам с кучей описательных параметров сделок в начале, которые не будут видны алгоритму. Поэтому нужно их транспонировать (обратите внимание, что функция транспонирования делает матрицу из датафрейма).

С помощью функции ncol() видно, что столбцы покупателей идут до 107, так что вы можете выбрать только векторы покупок в строках для каждого покупателя, транспонировав данные из столбцов с 8 по 107 и записав их в новую переменную под названием winedata.transposed:

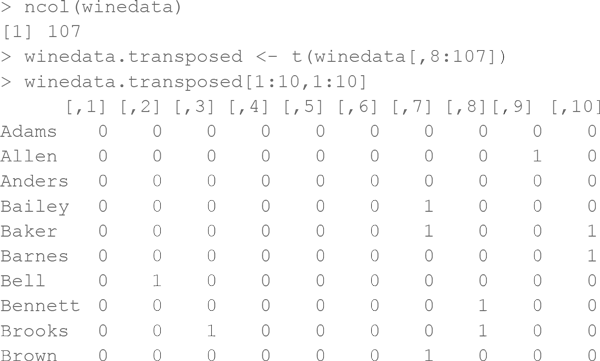
Примените функцию skmeans к набору данных, чтобы получить пять средних значений и использовать генетический алгоритм (похожий на тот, что мы использовали в Excel). Результаты запишите обратно в объект winedata.clusters:

> winedata.clusters <– skmeans(winedata.transposed, 5, method="genetic")

Обратившись затем к этому объекту из консоли, можно получить отчет о его содержимом (ваши результаты наверняка отличаются, ведь мы пользовались алгоритмом оптимизации):

> winedata.clusters

A hard spherical к-means partition of 100 objects into 5 classes.

Class sizes: 16, 17, 15, 29, 23

Call: skmeans(x = winedata.transposed, к = 5, method = «genetic»)

Вызывая str() для кластерного объекта, убедитесь, что текущие кластерные соотнесения хранятся в списке «cluster»:

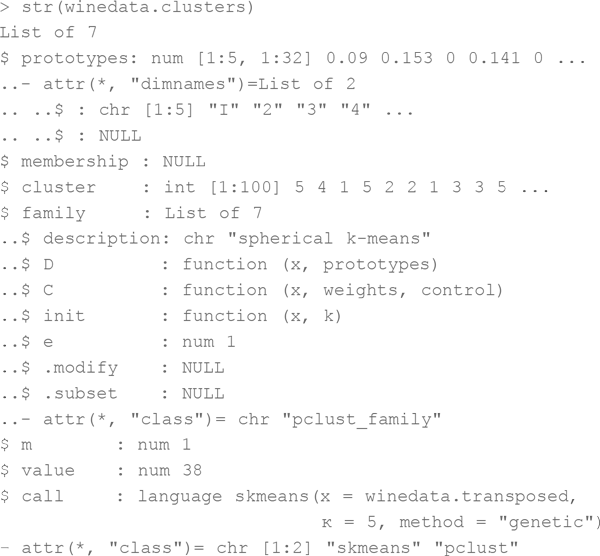
Если вы, к примеру, хотите посмотреть кластерное соотнесение для строки 4, используйте матричную запись кластерного вектора:

> winedata.clusters$cluster[4]

[1] 5

Каждая строка называется фамилией покупателя (вы сами их так назвали, когда читали их функцией read.csv()), так что соотнесения можно искать также по ним, пользуясь функцией row.names () вместе с which():

> winedata.clusters$cluster[

which(row.names(winedata.transposed)=="Wright")

]

[1] 4

Более того, если понадобится, вы можете выписать все эти кластерные отнесения функцией write.csv(). Воспользуйтесь ?, чтобы узнать, как она работает. Спойлер: очень похоже на read.csv().

Во время работы с Excel вы «расшифровывали» кластер, понимая поведение параметров описания сделок, определяющих их. Вы считали общее количество сделок, совершенных в каждом кластере, и сортировали их. Как сделать что-то подобное в R?

Для выполнения расчетов подойдет aggregate(), где в поле «by» нужно выбрать конкретные элементы кластера – то есть «собрать (aggregate – англ.) заказы по элементам». Также выберете тип группировки по своему желанию: сумму по сравнению со средним, минимумом, максимумом, медианой и т. д.:

aggregate(winedata.transposed,

by=list(winedata.clusters$cluster), sum)

Используйте транспонирование, чтобы сохранить эти значения в кластере в виде пяти столбцов (прямо как в Excel), – и вы обрежете первую строку группы, которая просто возвращает фамилии элементов кластера. Затем сохраните все это в переменной winedata.clustercounts:

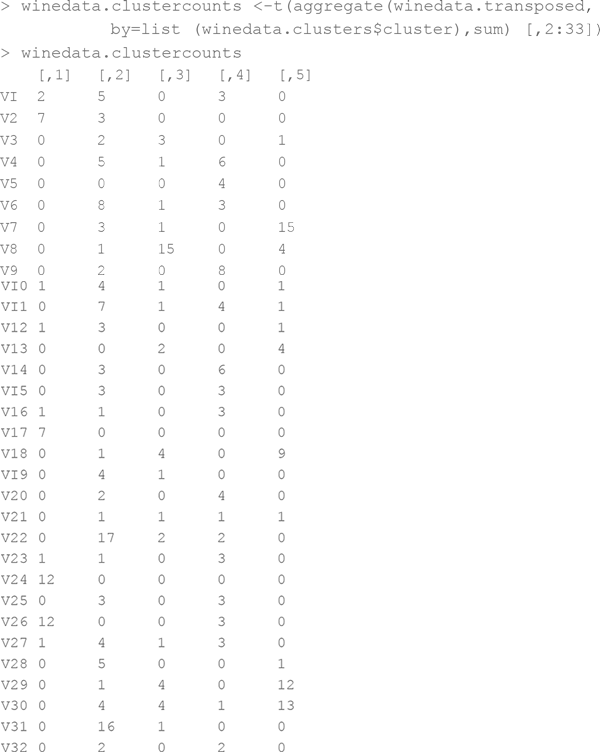
И вот, наконец, – количество сделок по кластерам. Приделаем эти семь столбцов описательных данных обратно к сделкам с помощью функции cbind():

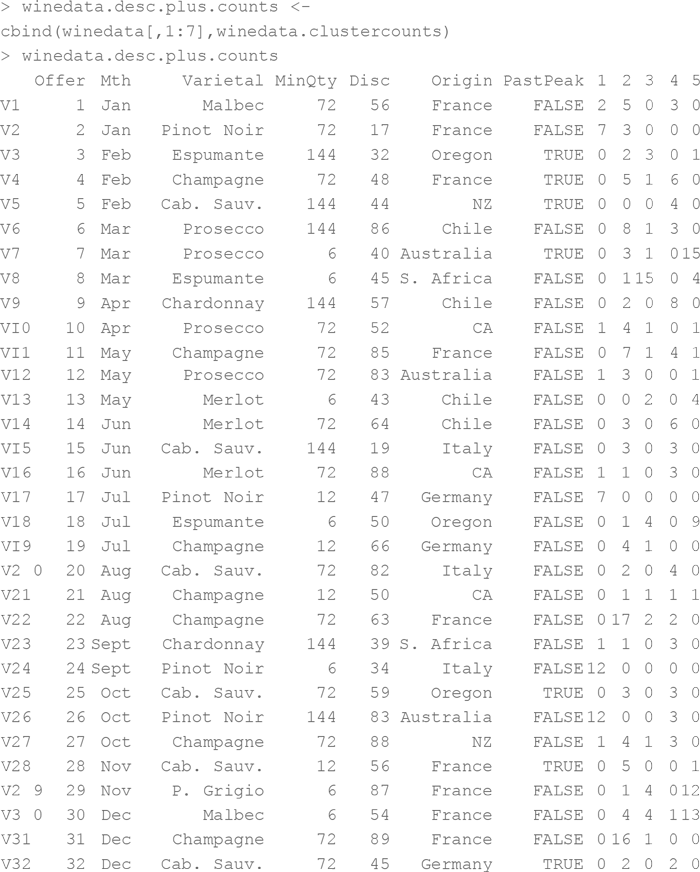
Также данные можно отсортировать функцией order() внутри скобок датафрейма. Вот сортировка для поиска самых популярных сделок для кластера 1. Обратите внимание: я поставил минус перед данными, чтобы отсортировать их по убыванию. Это можно сделать и другим способом – поставив флажок decreasing=TRUE в функции order():

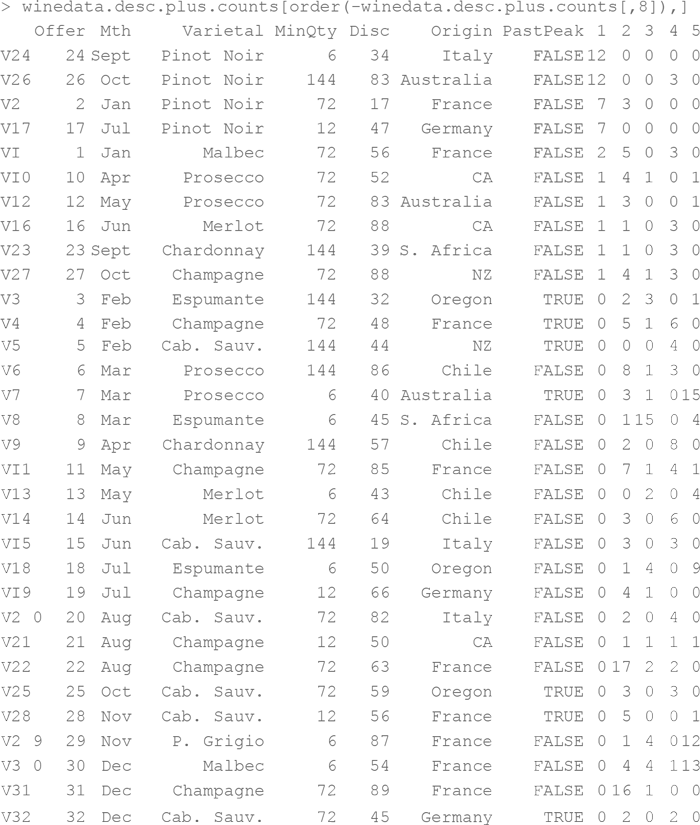
При взгляде на самые популярные ссылки становится ясно, что кластер 1 – это кластер пино нуар. (Напоминаю, что ваша нумерация может отличаться. Генетический алгоритм никогда не дает двух одинаковых решений подряд.)

А теперь, чтобы повторить все до конца, отбросив разглагольствования, прилагаю код, в котором написана в R большая часть главы 2 этой книги:

> setwd(«/Users/johnforeman/datasmartfiles»)

> winedata <– read.csv(«WineKMC.csv»)

> winedata[is.na(winedata)] <– 0

> install.packages(«skmeans»,dependencies = TRUE)

> library(skmeans)

> winedata.transposed <– t(winedata[,8:107])

> winedata.clusters <– skmeans(winedata

.transposed, 5, method="genetic")

> winedata.clustercounts <-

t(aggregate(winedata.transposed,by=list

(winedata.clusters$cluster), sum) [,2:33])

> winedata.desc.plus.counts <-cbind

(winedata[,1:7],winedata.clustercounts)

> winedata.desc.plus.counts[order

(-winedata.desc.plus.counts[,8]),]

Вот и все – от чтения данных из файла до анализа кластеров. Элементарно! Ведь обращение к функции skmeans() берет на себя большую часть сложных расчетов. Ужасно для обучения, прекрасно для работы.

Построение моделей ИИ для данных о беременных

Заметка

Файл CSV, использованный в этой части, Pregnancy.csv, доступен для скачивания на сайте книги, .

В этом разделе мы воспроизведем некоторые модели предсказания беременности из глав 6 и 7. Точнее, мы построим два классификатора с помощью функции glm() с логистической функцией связи, а также функции randomForest() (которая генерирует деревья, причем любые, от простых «пеньков» до полноценных деревьев принятия решений).

Обучающие и тестовые данные разделены на два файла CSV – Pregnancy.csv и Pregnancy_Test.csv. Сохраните их в своей рабочей директории, а потом загрузите в пару датафреймов:

>PregnancyDatа<-read.сsv(«Pregnancy.csv»)

>PregnancyData.Test<-read.csv(«Pregnancy_Test.csv»)

Чтобы «прочувствовать» эти данные, запустите над ними summary() и str(). Моментально становится очевидным, что данные пола и типа адреса были загружены как категорийные, но в выведенных функцией str() данных итоговая переменная (1 означает беременных, 0 – «не-беременных») также воспринимается как числовое значение вместо двух разных классов:

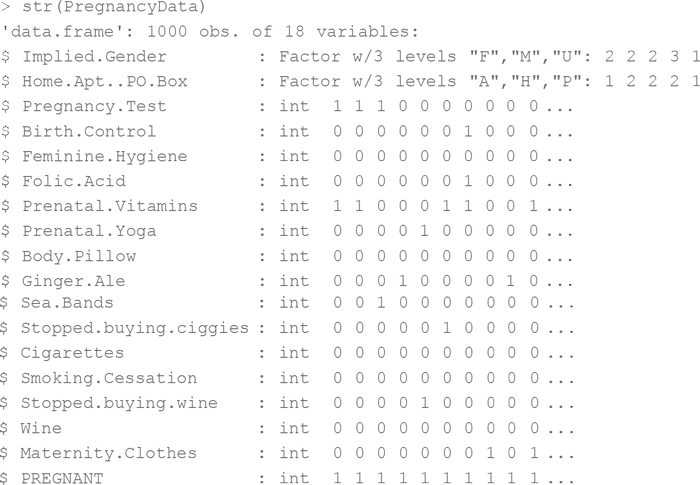
Отличная новость для randomForest() – мы факторизируем эту итоговую переменную в два класса (класс 0 и класс 1), и это значение уже не считается целочисленным! Делается это следующим образом:

PregnancyData$PREGNANT <– factor(PregnancyData$PREGNANT)

PregnancyData.Test$PREGNANT <– factor(PregnancyData.Test$PREGNANT)

Теперь суммирование столбца дает два счетчика элементов для каждого класса, при этом 0 и 1 считаются категориями:

Для построения логистической регрессии нужна функция glm(), встроенная в исходный пакет R. Для функции randomForest() вам понадобится инсталлировать пакет randomForest. Также неплохо было бы построить кривые ошибок, которые вы встречали в главах 6 и 7. Для таких графиков есть специальный пакет – ROCR. Установка этих двух пакетов займет совсем немного времени:

install.packages(«randomForest»,dependencies=TRUE)

install.packages(«ROCR»,dependencies=TRUE)

library(randomForest)

library(ROCR)

Ну что ж, данные внутри, пакеты загружены. Пришло время строить модель! Начнем с логистической регрессии:

> Pregnancy.lm <– glm(PREGNANT ~.,

data=PregnancyData,family=binomial(«logit»))

Функция glm() строит линейную модель, которую вы определили как логистическую регрессию, пользуясь опцией family=binomial(«logit»). Снабжение функции данными происходит через поле data=PregnancyData. Теперь вам, наверное, интересно, что значит PREGNANT ~. Это – формула в R. Она означает: «Обучи мою модель прогнозировать столбец PREGNANT с помощью остальных столбцов». Тильда (~) означает «с помощью», а период значит «все остальные столбцы». Конкретное подмножество столбцов также выбираются путем набора их названий:

> Pregnancy.lm <– glm(PREGNANT ~

Implied.Gender +

Home.Apt..PO.Box +

Pregnancy.Test +

Birth-Control,

data=PregnancyData,family=binomial(«logit»))

Но вы используете обращение PREGNANT~, потому что для обучения модели хотите использовать все столбцы.

После построения линейной модели взгляните на ее коэффициенты и проанализируйте, какие переменные имеют статистическую значимость (подобно проверке на критерий Стьюдента в главе 6), суммируя модель:

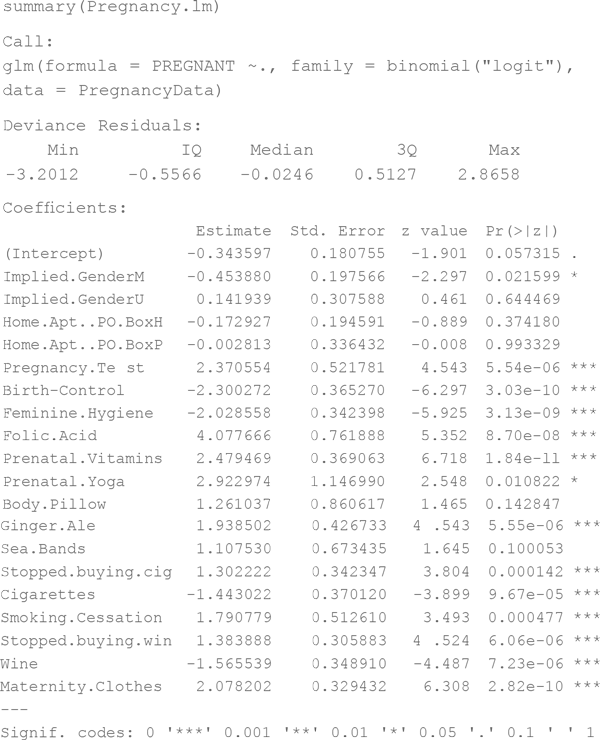
Коэффициенты, не имеющие хотя бы одного *, представляют собой сомнительную ценность.

Точно так же можно обучить модель случайного леса с помощью функции randomForest():

> Pregnancy.rf <-

randomForest(PREGNANT~.,data=PregnancyData,importance=TRUE)

Синтаксис в целом такой же, как и при вызове функции glm() (выполните ?randomForest, чтобы узнать больше о подсчете деревьев и глубине). Обратите внимание на значение importance=TRUE в вызове. Это позволит вам графически отобразить важность переменных с помощью другой функции, varImpPlot(), которая поможет понять, какие переменные важны, а какие не стоят внимания.

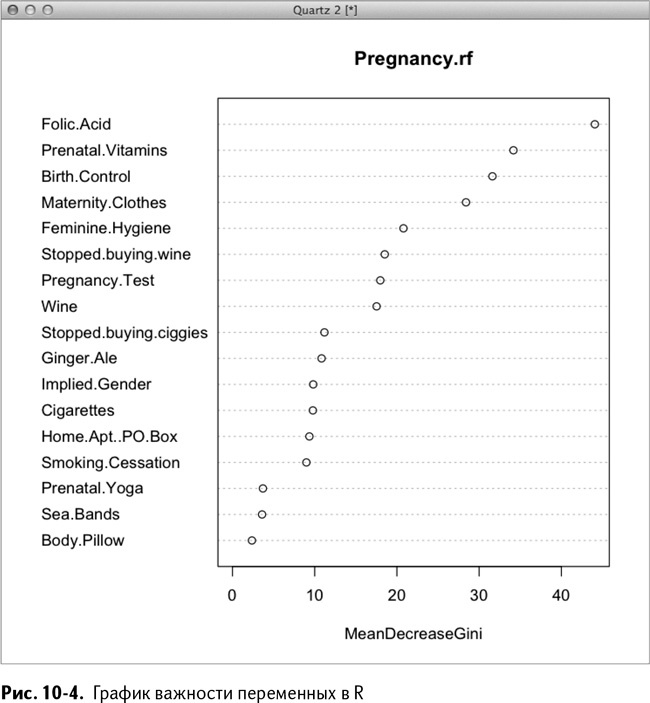
Пакет randomForest позволяет оценить вклад каждой переменной в снижение средней загрязненности. Чем он больше, тем важнее переменная. Можете воспользоваться этим, чтобы выбрать и убрать переменные, которые могут вам понадобиться для другой модели. Чтобы взглянуть на эти данные, используйте функцию varImpPlot() с type=2, ранжируя их согласно расчету загрязненности, приведенному в главе 7 (не стесняйтесь использовать команду ?, чтобы прочитать о разнице между type=1 и type=2):

varlmpPlot(Pregnancy.rf, type=2)

Все это приводит нас к графику ранжировки, изображенному на рис. 10-4. Фолиевая кислота выходит вперед вместе с витаминами и приемом противозачаточных.

Теперь, когда вы построили модели, можно приступить к прогнозированию – для этого в R есть функция predict(). Вызовите ее, сохранив результат в две разные переменные, чтобы можно было их сравнить. Принцип работы этой функции в целом таков, что она принимает модель, набор данных для прогнозирования и разные другие специальные опции:

> PregnancyData.Test.lm.Preds <-

predict(Pregnancy.lm,PregnancyData.Test,type="response")

> PregnancyData.Test.rf.Preds <-

predict(Pregnancy.rf,PregnancyData.Test,type="prob")

Вызвав predict дважды, вы увидите, что оба раза она работала с разными моделями, тестовыми данными и параметрами type, необходимыми данной модели. В случае линейной модели type="response" устанавливает значения прогноза между 0 и 1, как исходные значения PREGNANT. При работе со случайным лесом type="prob" обеспечивает нам уверенность в том, что в итоге мы получим классовые вероятности – два столбца данных: в одном вероятность покупателя оказаться беременным, в другом – «не-беременным».

Эти результаты выглядят немного по-разному, но, повторюсь, используются разные алгоритмы, разные модели и т. д. Важно «поиграть» с ними и почитать описания.

Вот отчет о результате прогноза:

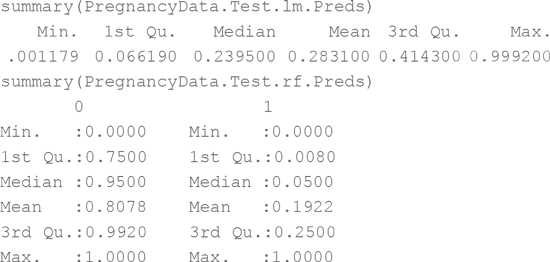
Второй столбец, из прогноза случайного леса, вероятностно ассоциирован с беременностью (а первый, соответственно, с ее отсутствием), так что он чем-то похож на прогноз логистической регрессии. С помощью квадратных скобок выберите отдельные записи или наборы записей, чтобы взглянуть на вводные данные и прогноз (я транспонировал строку, чтобы лучше смотрелось):

Обратите внимание: при выводе вводной строки я оставляю номер столбца пустым в квадратных скобках [1,], так что выводится вся строка целиком. Этот конкретный покупатель неизвестного пола, живущий в апартаментах, покупал браслеты от укачивания и вино, но вино затем покупать перестал. Логистическая регрессия дает ему 0,67 баллов, а случайный лес – 0,5. В данном случае покупательница действительно беременна – очко в пользу логистической регрессии!

Теперь у вас есть два вектора классовой вероятности для каждого из вариантов. Сравните модели в терминах действительно положительных значений и значений ложноположительных, как мы делали ранее в этой книге. К счастью для вас, пакет ROCR для R способен рассчитать и построить кривые ошибок, так что вам не придется заниматься этим вручную. Так как вы уже загрузили пакет ROCR, первое, что нужно сделать – это создать в нем два объекта предсказания с помощью функции ROCR prediction(). Эта функция считает количество прогнозов положительного и отрицательного классов на границах различных уровней классовых вероятностей:

> pred.lm <-

prediction(PregnancyData.Test.lm.Preds,

PregnancyData.Test$PREGNANT)

> pred.rf <-

prediction(PregnancyData.Test.rf.Preds[,2],

PregnancyData.Test$PREGNANT)

Обратите внимание: во втором вызове вы попадаете во второй столбец классовых вероятностей (прогноз случайного леса), как обсуждалось ранее. Затем можно превратить эти объекты прогнозирования в рабочие объекты ROCR, запустив над ними функцию performance(). Такой объект принимает классификацию, данную моделью в тестовом наборе для различных граничных значений, и использует их для построения кривой вашего выбора (в нашем случае кривой ошибок):

> perf.lm <– performance(pred.lm,"tpr" fpr")

> perf.rf <– performance(pred.rf,"tpr","fpr")

Заметка

Для любопытных: у performance() много других способностей, кроме tpr и fpr, например prec для точности и rec для отклика. Все они подробно описаны в документации ROCR.

Визуализируйте эти кривые функцией plot(). Сначала кривую линейной модели (флажки xlim и ylim используются для установки нижней и верхней границ по осям x и y):

> plot(perf.lm/xlim=c(0,1), ylim=c(0,1))

Кривую случайного леса можно построить, добавив флажок add=TRUE, чтобы наложить ее сверху, и lty=2 (lty – сокращение от line type, тип линии; подробнее можно узнать из описания функции ?plot):

plot(perf.rf/xlim=c(0,1), ylim=c(0,1), lty=2,add=TRUE)

На рис. 10-5 мы видим две линии: сплошную кривую линейной модели и пунктирную – модели случайного леса. По большей части логистическая регрессия превосходит выборку случайного леса, который вырывается вперед только в крайней правой части графика.

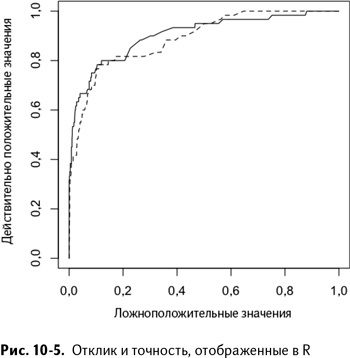
Итак, мы освоили две разные прогностические модели, использовали их на тестовом наборе и сравнили их точность и отклик с помощью следующего кода:

> PregnancyData <– read.сsv(«Pregnancy.сsv»)

> PregnancyData.Test <– read.csv(«Pregnancy_Test.csv»)

> PregnancyData$PREGNANT <– factor(PregnancyData$PREGNANT)

> PregnancyData.Test$PREGNANT <– factor(PregnancyData.Test$PREGNANT)

> install.packages(«randomForest»,dependencies=TRUE)

> install.packages(«ROCR»,dependencies=TRUE)

> library(randomForest)

> library(ROCR)

> Pregnancy.lm <– glm(PREGNANT ~.,

data=PregnancyData,family=binomial(«logit»))

> summary(Pregnancy.lm)

> Pregnancy.rf <-

randomForest(PREGNANT-.,data=PregnancyData,importance=TRUE)

> PregnancyData.Test.rf.Preds <-

predict(Pregnancy.rf,PregnancyData.Test,type="prob")

> varlmpPlot(Pregnancy.rf, type=2)

> PregnancyData.Test.lm.Preds <-

predict(Pregnancy.lm,PregnancyData.Test,type="response")

> PregnancyData.Test.rf.Preds <-

predict(Pregnancy.rf,PregnancyData.Test,type="prob")

> pred.lm <-

prediction(PregnancyData.Test.lm.Preds,

PregnancyData.Test$PREGNANT)

> pred.rf <-

prediction(PregnancyData.Test.rf.Preds[,2],

PregnancyData.Test$PREGNANT)

> perf.lm <– performance(pred.lm,"tpr","fpr")

> perf.rf <– performance(pred.rf,"tpr","fpr")

> plot(perf.lm,xlim=c(0,1), ylim=c(0,1))

> plot(perf.rf,xlim=c(0,1), ylim=c(0,1), lty=2,add=TRUE)

Действительно, довольно простой подход. Особенно если вспомнить сравнение двух разных моделей в Excel.

Прогнозирование в R

Заметка

Файл CSV, использованный в этом разделе, можно скачать с сайта книги, www.wiley.com/go/datasmart.

Этот раздел поистине безумен. Почему? Потому что мы регенерируем прогноз экспоненциального сглаживания из главы 8 так быстро, что голова кружится.

Для начала загрузим данные спроса на мечи в SwordDemand.csv и выведем его в консоль:

У нас загружено 36 месяцев спроса – просто и со вкусом. Первое, что нужно сделать – сообщить R, что это временной ряд данных. «Информатором» служит функция ts():

sword.ts <– ts(sword,frequency^12,start=c(2010,1))

Мы снабжаем функцию ts() данными, значением частоты (количество наблюдений в единицу времени; в нашем примере – 12 в год) и начальной точкой (в нашем примере – январь 2010).

Если вывести sword.ts на экран через терминал, R «запомнит», что его нужно выводить помесячно как таблицу:

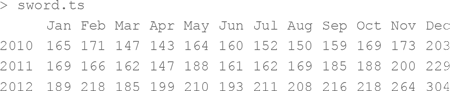
Отлично!

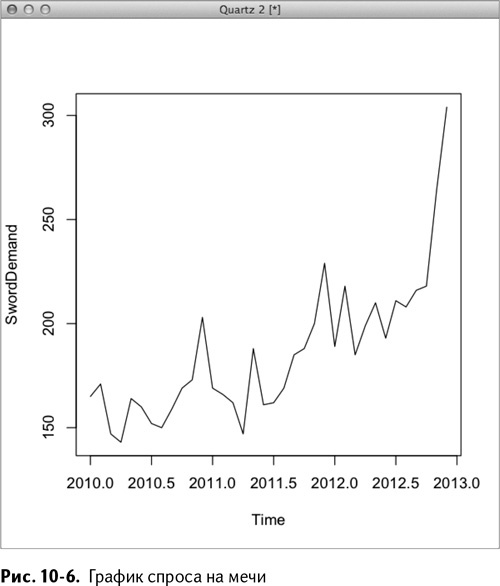
Также можно построить график:

> plot(sword.ts)

На этом этапе мы готовы прогнозировать, для чего отлично подходит пакет forecast. Смело ищите его на CRAN ( ) или послушайте, как автор рассказывает о нем на YouTube: .

Для прогнозирования с помощью этого пакета нужно вызвать функцию forecast() для объекта временного ряда. При этом функция сама определяет подходящий метод. Помните, как мы перебирали техники в главе 8? Функция forecast() сделает это за вас!

> install.packages(«forecast»,dependencies=TRUE)

> library(forecast)

> sword.forecast <– forecast(sword.ts)

Ну вот и все! Прогноз со встроенными прогностическими интервалами сохранен в объекте sword.forecast. Он выглядит так:

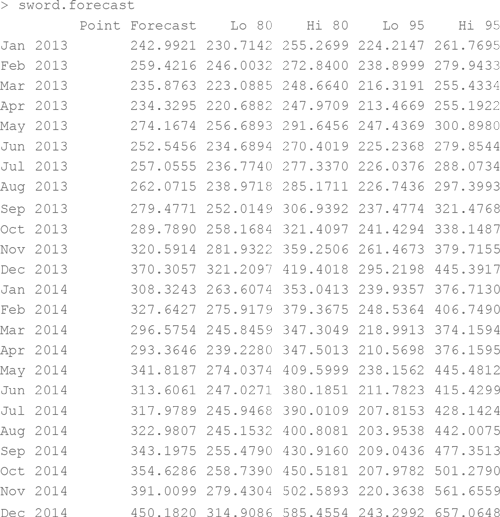
С тем, какой метод выбрал R, можно познакомиться, вбив значение «method» в объект sword.forecast:

> sword.forecast$method

[1] «ETS(M,A,M)»

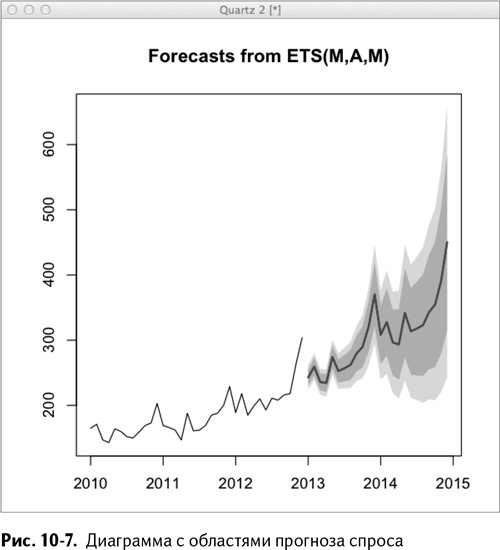
MAM означает мультипликативную погрешность, добавочный тренд и мультипликативную сезонность. Функция forecast() выбрала экспоненциальное сглаживание Холта – Винтерса. Вам не нужно вообще ничего делать! При построении автоматически получается диаграмма с областями, как на рис. 10-7:

plot(sword.forecast)

А вот код, повторяющий содержание главы 8:

sword <– read.csv(«SwordDemand.csv»)

sword.ts <– ts(sword,frequency=12/start=c(2010,1))

install.packages(«forecast»,dependencies=TRUE)

1ibrary(forecast)

> sword.forecast <– forecast(sword.ts)

> plot(sword.forecast)

Вот она – прелесть использования пакетов, написанных другими людьми, специально для таких задач!

Определение выбросов

Заметка

Файлы, использованные в этом разделе, PregnancyDuration.csv и CallCenter.csv, можно найти на сайте книги, .

В этом разделе мы повторим в R еще одну главу из книги, чтобы окончательно убедиться в том, насколько это просто.

Для начала считайте данные о продолжительности беременности из файла PregnancyDuration.csv, расположенного на сайте книги:

> PregnancyDuration <– read.csv(«PregnancyDuration.csv»)

В главе 9 мы вычисляли медиану, первый и третий квартили и внутренние и внешние границы Тьюки. Квартили можно получить простой функцией summary():

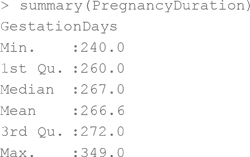
Межквартильный размах оказывается равным 272 минус 260 (другой способ – вызвать встроенную функцию IQR() для столбца GestationDays):

> PregnancyDuration.IQR <– 272–260

> PregnancyDuration.IQR <– IQR(PregnancyDuration$GestationDays)

> PregnancyDuration.IQR

[1] 12

Теперь рассчитайте нижние и верхние границы Тьюки:

> LowerInnerFence <– 260 – 1.5*PregnancyDuration.IQR

> UpperlnnerFence <– 272 + 1.5*PregnancyDuration.IQR

> LowerInnerFence

[1] 242

> UpperlnnerFence

[1] 290

Нам снова пригодится функция which() – для определения точек, вылезающих за границы, и их положения:

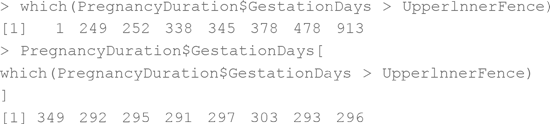
Конечно, один из лучших способов справиться с задачей – вызвать функцию boxplot(). Она отобразит медиану, первый и третий квартили, границы Тьюки, а также выбросы (при их наличии):

boxplot(PregnancyDuration$GestationDays)

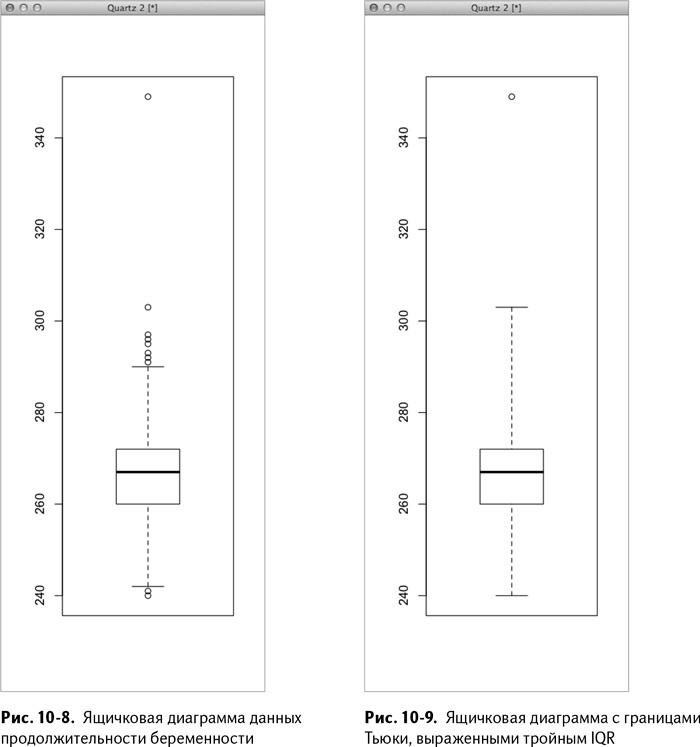
Так получается диаграмма, изображенная на рис. 10-8.

Границы Тьюки можно превратить во «внешние» границы, изменив флажок ранжировки при вызове функции boxplot() (по умолчанию там стоит 1,5, умноженное на IQR). Установите range=3 – тогда границы Тьюки проводятся по самым крайним точкам 3*IQR:

> boxplot(PregnancyDuration$GestationDays, range=3)

На рис. 10-9 видно, что выброс всего один – это пресловутая беременность миссис Хадлум сроком в 349 дней.

Также можно сделать и обратное – вывести данные с диаграммы в консоль. Список stats выдает границы и квартили:

А список out выводит значения выбросов:

> boxplot(PregnancyDuration$GestationDays,range=3)$out

[1] 349

Итак, это была задача об определении продолжительности беременности. Теперь перейдем к более сложной – поиску выбросов в данных о работе сотрудников службы поддержки. Данные эти находятся в файле CallCenter.csv на сайте книги. Загрузив и вызвав summary, получаем:

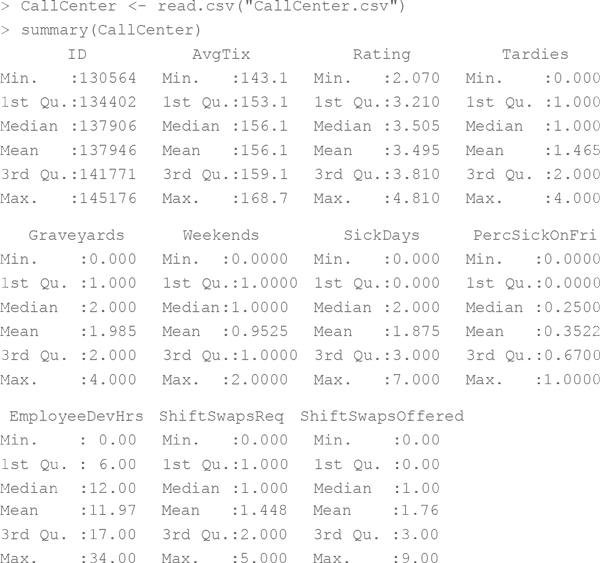
Как и в главе 9, необходимо нормализовать и отцентрировать данные. Для этого нужна только функция scale():

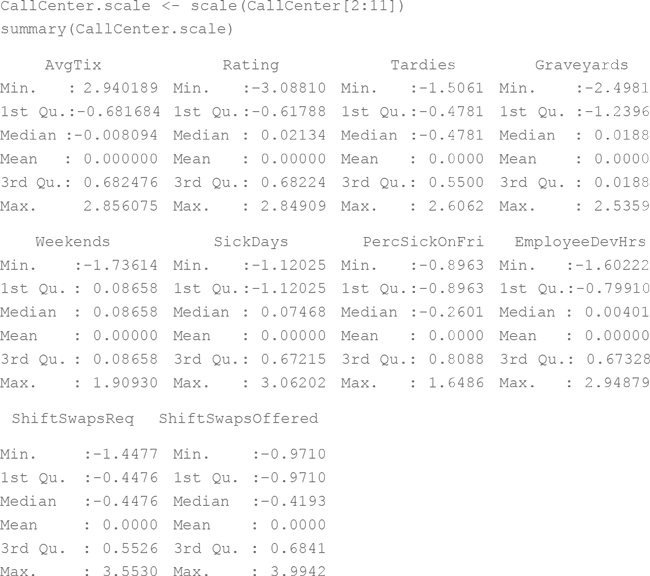
Подготовив данные, пропустите их через функцию lofactor(), которая находится в пакете DmwR:

install.packages(«DMwR»,dependencies=TRUE)

library(DMwR)

Вставьте данные и значение k (в этом примере 5, как и в главе 9) – и функция выдаст значения ФЛВ:

CallCenter.lof <– lofactor(CallCenter.scale,5)

Данные с самыми большими значениями (ФЛВ обычно несколько выше 1) – самые «выпуклые» точки. К примеру, можно выделить данные, ассоциированные с теми сотрудниками, чей ФЛВ превышает 1,5:

Это все те же два выдающихся сотрудника, которых мы уже встречали в главе 9. Но какая огромная разница в количестве строк кода, необходимых для данной операции:

> CallCenter <– read.csv(«CallCenter.csv»)

> install.packages(«DMwR»,dependencies=TRUE)

> library(DMwR)

> CallCenter.scale <– scale(CallCenter[2:11])

> CallCenter.lof <– lofactor(CallCenter.scale,5)

Вот и все!

Назад: Налаживаем контакт с R

Дальше: Подытожим