Мы уже упоминали выше, что обычное евклидово пространство определяется наличием двух структур: (i) оно представляет собой трехмерный континуум (т. е. его точки задаются тремя непрерывными координатами) и (ii) расстояние между двумя точками определяется простой формулой, следующей из теоремы Пифагора. Все другие структуры евклидова пространства можно вывести из этих двух фундаментальных свойств. Мы выяснили, что является аналогом первой структуры для пространства-времени специальной теории относительности: это четырехмерный континуум, точки которого (так называемые «события») задаются четырьмя непрерывными координатами – длиной, шириной, высотой и временем.

Остается определить, что служит аналогом понятия расстояния между двумя событиями. Этот аналог был введен Анри Пуанкаре и называется «пространственно-временным интервалом» между двумя событиями. Он определяется почти такой же простой математической формулой, как и расстояние между двумя точками в обычном пространстве. Формула основывается на кажущемся вполне невинном обобщении теоремы Пифагора, имеющем, однако, большие физические последствия: квадрат интервала между двумя событиями А и В равен сумме квадратов разностей значений координат А и В по длине, ширине и высоте минус квадрат разности временных координат А и В (умноженный на скорость света). В отличие от обычного евклидова пространства, где квадрат расстояния между двумя точками всегда дается суммой квадратов, каждый из которых входит со знаком плюс, здесь мы видим, что квадрат интервала содержит четыре члена: три квадрата входят со знаком плюс, тогда как квадрат четвертого – со знаком минус. Этот последний знак минус играет важную роль и имеет большое число физических последствий.

Во-первых, заметим, что из-за наличия минуса «квадрат интервала» между двумя событиями не всегда дает положительную величину (несмотря на то, что содержит в определении «квадрат»). Он может быть положительным, отрицательным или нулевым. Когда квадрат интервала между двумя событиями равен нулю, это означает, что два события могут быть связаны световым лучом (см. примечания к главе 1). Когда он отрицательный, это означает, что данные два события могут быть соединены мировой линией некоторого массивного объекта (какого-либо атома или наблюдателя), совершающего движение со скоростью, меньшей скорости света. В этом случае квадрат интервала между событиями после замены знака и деления на квадрат скорости света равен квадрату интервала времени между событиями для данного атома или наблюдателя, движущегося с постоянной скоростью. Наконец, в случае, когда квадрат интервала между двумя событиями положителен, существует некий наблюдатель, для которого эти два события одновременны и разделены пространственным расстоянием, квадрат которого равен квадрату интервала.

В целом мы видим, что квадрат интервала между двумя событиями в зависимости от его знака, по существу, измеряет либо квадрат расстояния, либо квадрат продолжительности времени (умноженный на квадрат скорости света). Мы также видим, что скорость света играет роль фактора перехода от продолжительности к расстоянию. Для простоты удобно использовать единицы, в которых нет необходимости явно вводить этот фактор. Для этого достаточно, например, измерять продолжительности в секундах, а расстояния – в «световых секундах». Напомним, что световая секунда означает расстояние, пройденное светом в течение секунды (так же, как «световой год» определяет расстояние, которое свет преодолевает за год). Световая секунда, таким образом, равна 300 000 км. В этих единицах скорость света равна 1 (т. е. одной световой секунде в секунду). В дальнейшем, как правило, мы будем использовать такие единицы измерения.

Понятие интервала между двумя событиями определяет то, что можно назвать «хроногеометрией» (или, если угодно, «хроногеометрией») пространства-времени, т. е. обобщение геометрии обычного пространства в том виде, как она определяется понятием расстояния между двумя точками. Геометрию пространства можно представить себе мысленно, изображая вокруг каждой точки P геометрическое место точек, находящихся на единичном расстоянии от точки P, т. е. сферу. Аналогично, хроногеометрию пространства-времени можно изобразить, представив вокруг каждого события P множество событий, разделенных с P единичным квадратом интервала. Однако, поскольку квадрат интервала между двумя событиями может быть положительным, отрицательным или нулевым, мы видим, что полное представление о хроногеометрии пространства-времени будет складываться из определения для каждой точки P форм, соответствующих трем типам событий: (i) события, разделенные с Р квадратом интервала, равным плюс один; (ii) события, разделенные с Р квадратом интервала, равным минус один; и (iii) события, разделенные с Р нулевым интервалом.

Эти множества событий не представляют собой сферы, как в случае евклидовой геометрии. Читатель найдет представление множеств (i), (ii) и (iii) на рис. 3. Заметим, что множество (iii) представляет собой двойной конус, состоящий из двух конусов, соединенных своими вершинами (один конус направлен «в верх» пространства-времени, т. е. к тому, что традиционно называется будущим, тогда как другой конус направлен «в низ» пространства-времени, т. е. к прошлому). Поскольку этот конус представляет собой события, связанные с событием Р посредством светового луча, он называется «световым конусом». Множество (i) имеет форму песочных часов (иными словами, выглядит как два конуса, соединенные своими вершинами, а затем деформированные таким образом, чтобы образовать горловину, через которую может сыпаться песок). Множество (ii) состоит из двух отдельных поверхностей: одна находится в верхней части светового конуса (направленного в будущее), а другая – в нижней его части (направленной в прошлое).

Рисунок 3, на котором представлена хроногеометрия пространства-времени, по своему виду напоминает то, что можно было бы назвать мировой шахматной доской. «Мир» в смысле Минковского означает пространство-время, тогда как структура «шахматной доски» определяет правила, разрешающие ходы между «клетками шахматной доски», т. е. между разными событиями пространства-времени. Например, световой конус указывает на возможность соединения двух событий посредством обмена световым лучом. Интересно также отметить, что шахматная доска состоит из фигур, напоминающих песочные часы. Временной поток отсутствует в пространстве-времени, однако каждые песочные часы напоминают нам о том, что даже в этом мире, существующем вне времени, структуры имеют вид необратимого потока. Возможно, Гераклит, представлявший себе время ребенком, играющим в шахматы, как свидетельствует эпиграф к этой главе, оценил бы такой образ мировой шахматной доски.

Мировая шахматная доска Минковского ничего не содержит. Она представляет собой пространственно-временной фон, который обрамляет существование материи и ее взаимодействия. Чтобы придать наблюдаемое значение хроногеометрии этого мира, необходимо заполнить его объектами, способными почувствовать эту хроногеометрию. Напомним, что, как и в приведенном выше примере мира насекомых на полу, объект, такой как насекомое, имеющий заметную продолжительность жизни, оставляет след в виде трубы, проходящей снизу вверх в пространстве-времени. Жизнь человека также описывается подобной пространственно-временной трубой (рис. 4). Эта труба соответствует ходулям в приведенном выше отрывке из Пруста. Отметим также, что интуиция Пруста не обманула: эта труба занимает место, гораздо более значительное во времени, нежели в пространстве.

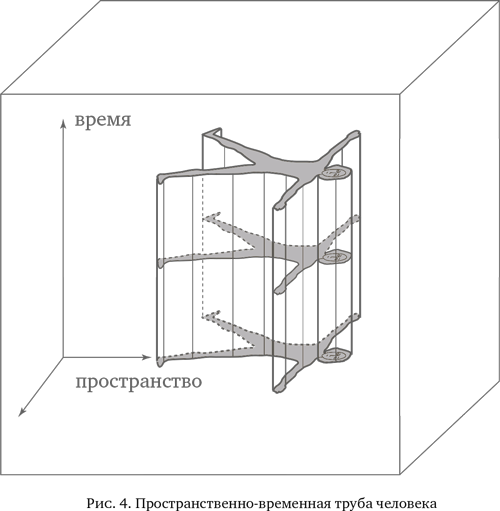
Действительно, при измерении, как уже говорилось, продолжительности в секундах, а расстояния в световых секундах эта труба имеет (временную) высоту в несколько миллиардов секунд, а ее (пространственная) ширина составляет лишь несколько миллиардных долей одной световой секунды. Другими словами, соотношение между высотой и шириной составляет порядка миллиарда миллиардов. В предельном случае, когда рассматриваемый объект обладает очень малыми пространственными размерами, скажем атом или элементарная частица, его пространственно-временная трубка сводится к обычной линии, толщиной которой можно пренебречь. Эта пространственно-временная линия пересекает пространство-время снизу вверх и заканчивается лишь там, где данная частица появляется или исчезает (см. пример на рис. 3).

Наконец, важно понять, что происходит с парадоксом близнецов в пространстве-времени. Для понимания сути этого явления необходимо рассмотреть хроногеометрию пространственно-временного треугольника. Пусть это будет пространственно-временной треугольник ABC (рис. 5). Стороны треугольника представляют собой пространственно-временные линии, связанные с парой часов идентичного производства. Первые часы идут вдоль стороны AC (направленной «по времени», т. е. соответствующей отрицательному квадрату интервала), в то время как вторые часы идут изначально вдоль стороны AB, а затем вдоль стороны BC (обе эти стороны также направлены по времени). Тот факт, что стороны АВ и ВС наклонены по отношению к стороне AC, соответствует при разложении пространства-времени на обычное пространство и время утверждению, что вторые часы, положение которых совпадало с положением первых в начале (а именно в событии A), начинают удаляться, а затем приближаются с постоянной скоростью, пока не встретятся снова в пространственно-временной точке C.

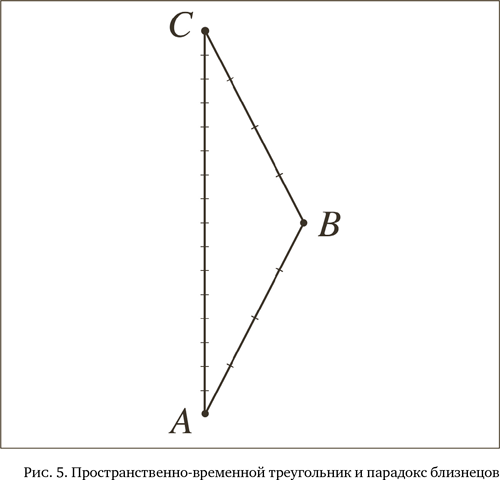
Согласно теории относительности, длительность жизни часов определяется исключительно суммарным интервалом вдоль пространственно-временной линии часов. Таким образом, первые часы будут отсчитывать длительность, равную длине (в смысле Минковского) стороны AC, а вторые – суммарную длину двух других сторон треугольника: AB + BC. Хроногеометрия пространства-времени, т. е. форма «песочных часов», определяющая мировую шахматную доску, говорит нам, что суммарный интервал сторон треугольника AB + BC короче интервала, соответствующего третьей стороне AC. Иначе говоря, количество тиков вторых часов, перемещающихся из A в В, а затем из B в С, меньше числа тиков первых часов, выбравших прямой маршрут в пространстве-времени из A в С. Данное «пространственно-временное неравенство треугольников» имеет противоположенный эффект, нежели неравенство треугольников обычного евклидова пространства, согласно которому сумма сторон всегда длиннее третьей стороны. Это различие вызвано особенностью формы пространственно-временной хроногеометрии, в которой теорема Пифагора содержит один знак минус для квадратов сторон прямоугольного треугольника, направленных по времени.

Независимо от вопроса о том, длиннее прямой путь или короче, чем непрямой, принципиальным моментом является то, что само существование геометрической интерпретации продолжительности жизни часов указывает на отсутствие абсолютного универсального времени. Согласно Ньютону, абсолютное время имеет универсальный и равномерный темп во всем пространстве, для всех часов и всех живых организмов, чувствующих «течение времени». Согласно Эйнштейну, временного потока не существует и каждые часы «видят собственное время», которое просто измеряет «длину» их пространственно-временной линии. Поэтому сколько разных часов, столько же разных времен.