Таким образом, совместное измерение Алисы дает случайный результат. В зависимости от этого результата либо фотон Боба всегда будет давать результат, который бы дал исходный фотон при измерении в том же направлении, либо он будет давать результат, противоположный потенциальному результату исходного фотона. Эти две ситуации равновероятны, и до этого момента Бобу не очень интересно участвовать в эксперименте. У него есть один шанс из двух получить такой же результат, который бы дал исходный фотон, и один шанс из двух на противоположный результат. Чтобы добиться этого, Бобу вообще ничего не надо делать: он же знает, что при всего двух возможных результатах вероятность правильного – 50 %. Но в процессе квантовой телепортации Алиса уже знает результаты собственного совместного измерения, поэтому ей заранее известно, какой результат измерения получит Боб. Следовательно, чтобы закончить процесс квантовой телепортации, Алиса должна сообщить Бобу о положении его дел.

Теперь нам становится понятно, как квантовая телепортация уходит от передачи сигнала на произвольных скоростях: процесс закончится только тогда, когда Боб получит информацию о результате совместного измерения, запутывающего два фотона Алисы. Эта коммуникация между Алисой и Бобом необходима, потому что без нее результаты измерений Боба будут чисто случайными, и он не сумеет их истолковать. Алиса передает информацию о результатах своих измерений по классическому каналу со скоростью света или медленнее. Но передача результата Алисы с необходимостью идет со скоростью света или медленнее. Следовательно, квантовая телепортация – от начала до конца – не идет со скоростью выше скорости света. Да, когда Алиса выполняет свое совместное измерение, что-то загадочное происходит на стороне Боба: его фотон переходит из неопределенного состояния в одно из двух возможных. Но Боб не может об этом узнать, ведь какое бы измерение он ни провел, его результат будет просто случайным. Но как только Алиса сообщает ему, в каком из двух состояний находится его фотон, Боб узнает, что он должен делать, чтобы систематически получать тот же результат, который получила бы Алиса, если бы выполнила измерение на своем исходном фотоне. Так фотон Боба оказывается в квантовом состоянии исходного фотона.

Заметьте, что Бобу совсем не обязательно измерять свой фотон. Он может сохранить его в целости на будущее и даже телепортировать куда-то еще. Можно вообразить целую телепортационную сеть с узлами, расположенными где-то в пятидесяти километрах друг от друга – на это расстояние эффект запутанности хорошо распространяется по оптоволокну. Если Боб узнает от Алисы, что его фотон всегда будет выдавать противоположный результат, Боб должен просто развернуть свой фотон. Это можно сделать, не тревожа частицу, потому что Боб переориентирует поляризацию фотона, но не получает никакой информации о его состоянии. Заметим также, что Боб может телепортировать свой фотон дальше без «выпрямления». Необходимо лишь сообщить получателю, что тому нужно провести инверсию самому. В итоге конечный получатель рассчитает, сколько раз ему нужно развернуть фотон. Если это нечетное число, то нужно развернуть фотон один раз, а если четное, то не нужно и этого.

Важно еще вот что. Ни Алиса, ни Боб ничего не знают о телепортированном квантовом состоянии исходного фотона. Результат совместного измерения Алисы над двумя фотонами всегда совершенно случаен. Он не дает информации о квантовом состоянии, которое мы телепортируем, и это не должно нас удивлять. Мы видели, что если мы имеем дело с запутанным состоянием, то результат измерения в любом конкретном направлении всегда совершенно случаен – в том смысле, что он нередуцируемо случаен. И наоборот, если мы начинаем с поляризованного фотона, каким бы ни было направление поляризации, и спрашиваем: «Ты такой же?» – результат будет также совершенно случайным в указанном смысле. В некотором смысле это обратные по отношению друг к другу процессы. Рассуждая дальше, мы видим, что это абсолютно необходимо. Если бы Алиса и/или Боб могли узнать что-то о телепортируемом состоянии, они бы могли повторять процесс, телепортируя его взад и вперед, используя каждый раз новую пару запутанных фотонов, пока не накопили бы достаточно информации, чтобы воспроизвести точную копию этого состояния, а это противоречило бы теореме о невозможности клонирования (см. главу 4).

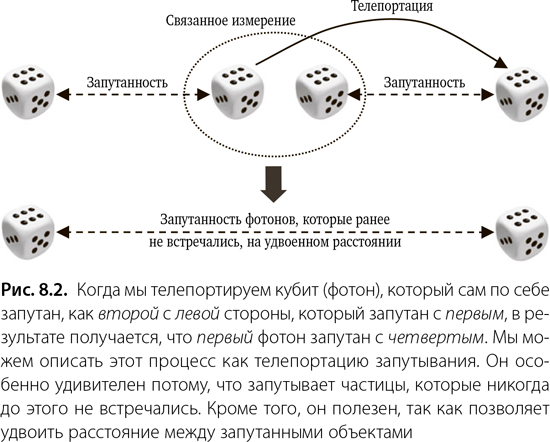
И наконец, Алиса и Боб могут телепортировать состояние фотона, который сам запутан с неким четвертым фотоном. Так как они ничего не узнают о телепортируемом состоянии, то не разрушают телепортируемую запутанность. Так мы используем оба аспекта запутанности: дважды для того, чтобы создать корреляцию разнесенных в пространстве фотонов, и один раз при совместном измерении. Мы можем запутать фотоны, которые никогда не встречались друг с другом и не имеют общего прошлого, как показано на рис. 8.2. В этом случае можно говорить о телепортации запутанности.