Книга: Для юных физиков. Опыты и развлечения (сборник)
Назад: 4. Немного арифметики на спичках
Дальше: 6. Немного физики на спичках
5. Немного геометрии на спичках
Горизонтально и вертикально
Задача 32-я
Попросите товарища положить на стол одну спичку горизонтально. Он положит, разумеется, так:
Рис. 44.
Затем попросите его положить возле первой спички вторую спичку вертикально. Сделает он это примерно так:  Рис. 45.
Рис. 45.
Товарищ ваш и не подозревает, что вы его «поддели». Боюсь, что вы и сами этого не подозреваете.
Ведь задача-то решена неверно!
Решение Обе спички (рис. 45) горизонтальны! Вы удивлены? Но подумайте: спичка, лежащая на горизонтальнойповерхности стола, может ли иметь вертикальноенаправление? Вертикальное направление – это направление сверху вниз, к земле(точнее, к центру земного шара), – а как бы вы ни положили спичку на стол, она не будет направлена к земле.

Девяносто девять человек из ста делают эту ошибку, – не исключая даже и иных математиков. Едва ли ваш товарищ будет тот сотый, который не попадет впросак. Два четырехугольника Задача 33-я 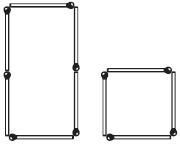 Рис. 46.
Рис. 46.
На рис. 46 изображен четырехугольник из 6 спичек, площадь которого вдвое больше площади квадрата со стороною, равною одной спичке.

Так как длина спички вам известна – 5 см, то вы легко определите площадь вашего четыреугольника в сантиметрах: 5x10=50 кв. см. Задача состоит в следующем: не изменяя длины обвода [25] этого четырехугольника, изменить форму его так, чтобы площадь его уменьшилась вдвое, т. е. равнялась 25 см. Как это сделать? 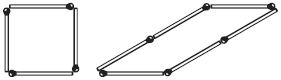 Рис. 47.
Рис. 47.
Пусть читатель обратит внимание на то, что речь идет о составлении четырехугольнойфигуры (а не непременно прямоугольной): углы новой фигуры не обязательно должны быть прямые.
Решение Надо из 6-ти спичек сложить параллелограммтак, чтобы его высота равнялась одной спичке (рис. 47). Такой параллелограмм, имеющий одинаковые основание и высоту с квадратом, должен иметь и одинаковую с ним площадь.

Что больше? Задача 34-я 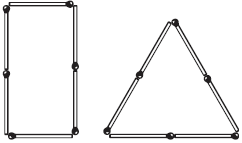 Рис. 48.
Рис. 48.
Из 6-ти спичек сложены прямоугольник и равносторонний треугольник. Обводы этих фигур, конечно, одинаковы. А у какой больше площадь? (рис. 48).

Решение 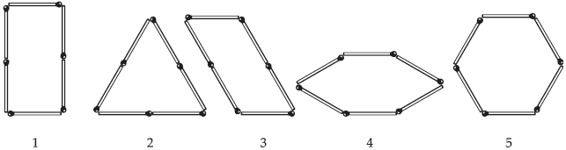 Рис. 49.
Рис. 49.
Чтобы решить эту задачу, надо знать, как вычисляется площадь треугольника: умножают длину основания на высоту и полученное произведение делят пополам; или – что то же самое – умножают половину основания на высоту. В нашем треугольнике половина основания = одной спичке, т. е. основанию прямоугольника. Если бы высоты этих фигур были одинаковы, то обе фигуры имели бы равные площади. Но легко видеть, что высота треугольника меньше двух спичек, т. е. меньше высоты прямоугольника. Значит, и площадь треугольника меньшеплощади прямоугольника.
Фигура с наибольшей площадью Задача 35-я Сейчас мы составили из 6-ти спичек прямоугольник и равносторонний треугольник. Но из того же числа спичек можно составить еще и другие фигуры, имеющие одинаковый обвод. Некоторые из этих фигур изображены на рис. 49.

Площади всех этих фигур различны. Спрашивается, у какой же из них площадь наибольшая? Решение 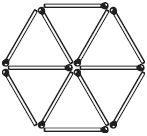 Рис. 50.
Рис. 50.
Мы уже знаем, что площадь фиг. 1 больше площади фиг. 2. Легко сообразить, что она больше также и площади фиг. 3 (сравните их высоты!). Остается, следовательно, сравнить по величине площади фигур 1, 4 и 5. Мы можем рассматривать все три фигуры, как шестиугольники с равными сторонами (у фиг. 1 два угла выпрямлены). В курсах геометрии доказывается, что из всех многоугольников с одинаковым числом сторон и одинаковым обводом наибольшую площадь имеет многоугольник правильный,т. е. такой, у которого равны не только стороны, но и углы. Этому условию удовлетворяет фигура 5; она, следовательно, и имеет наибольшую площадь, какую можно ограничить шестью спичками [26] .
Покажем кстати, как можно сложить из спичек правильныйшестиугольник. Для этого нужно примкнуть друг к другу 6 равносторонних треугольников, как показано на рис. 50, и затем вынуть внутренние спички.

Мост из двух спичек Задача 36-я  Рис. 51.
Рис. 51.
На рис. 51 вы видите остров, окруженный каналом. Ширина канала как раз равна длине одной спички, так что перебросить мостик через канал с помощью одной спички нельзя: невозможно опереться концами о берега канала.

Не удастся ли вам перекинуть мост через канаву с помощью двух спичек? Помните, однако, что склеивать или связывать эти две спички не полагается. Решение  Рис. 52.
Рис. 52.
Решение этой задачи основано на том, что длина линии, соединяющей противоположные углы квадрата (так называемая диагональ),меньше длины 1 1/2 спичек (см. рис. 52).

Зная это, мы можем построить требуемый мост так, как показано на рис. 53, – т. е. одну спичку кладем в положение 5–6, а другую в положение 7–4. Расстояние 2–7 очевидно равно расстоянию 5–7; расстояние 2–4, т. е. диагональ квадрата, меньше длины полутора спичек; а так как расстояние 2–7 равно половине спички, то пролет 7–4 короче длины спички. Отсюда и вытекает возможность сооружения нашего моста. 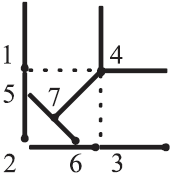 Рис. 53.
Рис. 53.

Задача эта может оказаться и практически полезной в том случае, когда, имея две одинаковые жерди, нужно перебросить (не связывая их между собою) мост через канаву, ширина которой как раз равна или даже чуть больше длины одной жерди. Возможно это, впрочем только в том месте канавы, где она поворачивает под прямым углом (рис. 54). 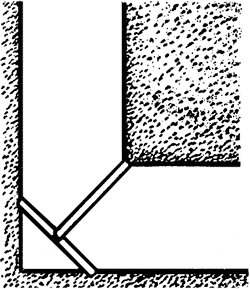 Рис. 54.
Рис. 54.

В витрине спичечного треста Задача 37-я  Рис. 55.
Рис. 55.
В витрине магазинов спичечного треста нередко выставляют ради рекламы огромные спичечные коробкй, по фасону совершенно подобные обыкновенным; а внутри коробка видны столь же чудовищные спички. Предположим, что такой коробок в 10 раз длиннее обыкновенного. Спрашивается:
1) сколько весит одна исполинская спичка, принимая вес обыкновенной спички в 1/10 грамма?
2) сколько спичек обыкновенного размера мог бы вместить один коробóк-великан?
Ответ, что спичка-великан весит (1/10) x 10, т. е. всего один грамм, – конечно, явно несообразен: ведь это чуть не настоящее полено – правда, всего в 2 см толщины, зато в полметра длины!
Так же несообразно допустить, что в огромном коробкé всего вдесятеро больше спичек, чем в обыкновенном, – т. е. столько, сколько в 10 коробках. Десять выложенных в ряд коробков не похожи на тот внушительный ящик, который выставлен в витрине.
Каковы же правильные ответы?
Решение Огромная спичка не только в 10 раз длиннее обыкновенной, но и в 10 раз толще и шире; следовательно, она превышает обыкновенную спичку по объему в 10x10x10, т. е. в 1000 раз. Отсюда определяем вес ее:
(1/10) x 1000 = 100 граммов.
Точно так же коробок-великан вместительнее обыкновенного в 1000 раз, и, значит, в него может войти около 50.000 обыкновенных спичек.
Высотомер из спичечного коробкá Высотомерами называются инструменты, посредством которых можно определять высоту предметов – дерева, столба, башни, – не взбираясь на их вершину. Лесничий всегда имеет при работе удобный инструмент такого рода, нередко карманного размера, для измерения высоты деревьев. Вы можете также обзавестись небольшим удобным дальномером, смастерив его из обыкновенного спичечного коробка. Вам понадобится для этого даже и не весь коробок, а только его наружная часть.
Чтобы приспособить ее для дальномера, нужно прежде всего ее укоротить, сделав длину равной ширине. Отрезав лишнюю часть коробка, как показано на рис. 55 и 56, надо заклеить отверстия полоской бумаги. У короткого края заклеенного прямоугольника проделывают небольшое отверстие – примерно в полсантиметра.

Этим исчерпывается изготовление дальномера. Объясним теперь, как им пользоваться для измерения высот. 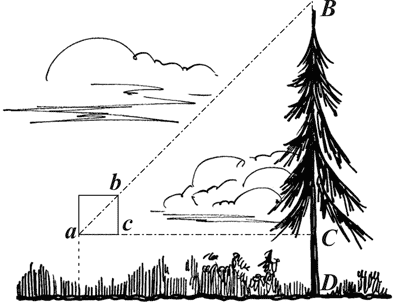 Рис. 57
Рис. 57
Пусть вы желаете измерить высоту дерева BD(рис. 57). Вы становитесь на некотором расстоянии от дерева и, держа дальномер так, чтобы нижний край его (близ которого устроено отверстие) располагался горизонтально, смотрите через отверстие на верхушку дерева. Приближаясь к дереву или удаляясь от него, отыскиваете такое место, стоя на котором вы увидите через дырочку аверхушку дерева В,как бы касающуюся верхнего края Ьспичечного коробка (рис. 58). Найдя это место, вам остается лишь измерить расстояние аСот этого места до основания дерева: тем самым вы определите и высоту дерева. Точнее говоря, не полную высоту дерева, а лишь высоту его над горизонтальной линией аС,проведенной на уровне ваших глаз; остается прибавить только кусок СD,который легко измерить непосредственно.


(Из рисунка 57 нетрудно понять, почему это так. Расстояние Ьсравно расстоянию ас– мы ведь так обрезали коробок. Из геометрии мы знаем, что при этом должны равняться между собою также и расстояния ВСи аС.)Успех измерения зависит в значительной мере от того, удалось ли удержать коробок так, чтобы асбыло горизонтально (или – что то же самое – чтобы Ьсбыло отвесно). Только тогда длина ВСбудет действительно равна аС.Чтобы обеспечить отвесное положение Ьс,можно прикрепить близ края коробкá небольшой отвес из нити с тяжелой бусиной (или пломбой) на конце.
Назад: 4. Немного арифметики на спичках
Дальше: 6. Немного физики на спичках

