Книга: Психология профессиональной пригодности
Назад: Глава 9. Методические приемы психологического обследования
Дальше: Раздел III. Результаты экспериментальных исследований и практические рекомендации по определению профессиональной пригодности
Глава 10. Приемы разработки и оценки методов диагностики и прогнозирования профессиональной пригодности
10.1. Показатели оценки профессиональной пригодности учащихся
Для определения прогностической ценности методик оценки и прогнозирования профессиональной пригодности необходимо иметь эффективные внешние критерии, то есть провести сравнение результатов экспериментально-психологического обследования с характеристиками успешности профессионального обучения (эффективность приобретения и закрепления знаний, умений и навыков) и реальной профессиональной деятельности.
Суммируя результаты оценок, выставляемых учащимся высших учебных заведений в процессе теоретического обучения на зачетах и экзаменах, по результатам обучения на тренажерах, по состоянию здоровья и физической подготовленности, необходимо помнить, что в ряде случаев текущие оценки могут играть роль «стимулирующего» фактора, то есть могут быть несколько завышенными или заниженными по сравнению с истинным уровнем знаний, умений и практических навыков. Характер оценок определяется также субъективными критериями инструкторов и преподавателей, и поэтому они могут существенно различаться. В связи с этим необходимо использовать несколько независимых показателей успешности профессионального обучения с последующим выделением ведущего критерия (оценка профессиональных способностей) и обобщающей оценки успешности обучения в вузе.
Например, при обучении курсантов летных училищ для выделения ведущего критерия используется ряд показателей успешности освоения программы летного обучения по курсам, типам самолетов (отдельно для учебного самолета первоначального летного обучения и выпускного учебно-боевого самолета) и за весь период обучения в училище в целом.
Профессиональная характеристика отражает успешность освоения программы профессионального обучения на каждом курсе (профессиональная подготовка, практика, контрольные задачи, самостоятельная работа в нормальных условиях и в усложненной обстановке). Характеристика курсантов-летчиков должна, в частности, включать такие параметры, как переносимость летной нагрузки, организация внимания в полете, координация движений, осмотрительность, реакция на отклонения; стойкость закрепленных навыков; знание и соблюдение законов, регламентирующих летную работу; соблюдение условий безопасности полетов, действий в особых случаях и содержать выводы о летных качествах и способностях курсанта; целесообразности его дальнейшего летного обучения по профилю училища.
Практика показывает, что на хороших и отличных студентов (курсантов) характеристики составляются достаточно объективно. В отношении же слабоуспевающих лиц, выявление которых наиболее важно для разработки, например, вопросов психологического отбора, допускается много субъективизма: недостатки нередко сглаживаются или опускаются, а в отдельных случаях (если студент, курсант не отчисляется, а остается для дальнейшей учебы) истинная картина прямо искажается. Поэтому к официальным профессиональным характеристикам как критерию способностей следует относиться с большой осторожностью.
В авиационной практике оценки в летных книжках выставляются инструктором за выполненные упражнения (задачи) и обобщаются каждый летный день. Теоретически считается, что при этом используется общепринятая 5-балльная шкала. Однако, как правило, оценки «1» и «2» не записываются. Согласно существующему положению переводить курсанта на следующую задачу можно в том случае, если предыдущую он освоил не ниже, чем на «хорошо». Таким образом, шкала оценок фактически сводится до 2-балльной. Наконец, использование оценок для формирования уверенности, бдительности, а также некоторые другие специфические для авиации обстоятельства не всегда соответствуют поставленным баллам «4» или «5». Поэтому, как показывает опыт, оценки в летных книжках курсантов не отражают истинного положения вещей и непригодны для использования в качестве внешних критериев летных способностей.
Более информативными являются оценки за выполнение практических задач. Результаты вывозного налета – количество полетов и время до первого самостоятельного вылета на каждом вновь осваиваемом типе самолета – характеризуют быстроту овладения летными навыками. Субъективность определения готовности к самостоятельному вылету сглаживается, с одной стороны, теми обстоятельствами, что ни один летчик-инструктор не выпустит в «воздух» курсанта, не будучи уверенным, что он сможет благополучно завершить полет. С другой стороны, летчик-инструктор не станет давать полетов больше необходимого минимума, так как их количество в определенной степени характеризует профессиональное и педагогическое мастерство самого инструктора, его авторитет, а завершение вывозной программы значительно облегчает его последующую работу. Кроме того, разрешение на самостоятельный вылет курсанта дает только командир эскадрильи, который, естественно, ко всем курсантам подходит с одинаковой меркой.
У разных командиров эта мерка неизбежно различна. К тому же на готовность курсантов к самостоятельному вылету сильно влияют пропуски летных дней из-за погодных условий и других обстоятельств. Это затрудняет сравнение курсантов, летающих с разных аэродромов, а также курсантов одних и тех же курсов за несколько лет и делает практически невозможным сравнение курсантов разных училищ, не говоря уже о тех случаях, когда сравнивается вывозная программа на неодинаковых типах самолетов.
Перечисленные недостатки устраняет сравнение полученного налета в нормированном отклонение по формуле
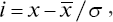
где x – фактический налет курсантов; 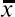 – средний налет в эскадрильи; σ – среднее квадратическое отклонение [72].
– средний налет в эскадрильи; σ – среднее квадратическое отклонение [72].
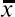 – средний налет в эскадрильи; σ – среднее квадратическое отклонение [72].
– средний налет в эскадрильи; σ – среднее квадратическое отклонение [72].Формула позволяет сравнивать налет отдельных курсантов по величине их отклонения от среднего налета в эскадрилье в единой системе координат. Например: курсант А из первой эскадрильи совершил 105 полетов до первого самостоятельного вылета, а курсант Б на другом аэродроме – 107 полетов. Средний налет и среднее квадратическое отклонение у курсантов соответственно равны 115 и 20, 123 и 22. В соответствии с этим налет в нормированном отклонении для курсанта А равен – 0,5, а для курсанта Б – 0,73. В данном случае налет курсанта Б лучше, чем у курсанта А, хотя фактический налет свидетельствует об обратном.
Коэффициент корреляции между количеством вывозных полетов и их временем, рассчитанный на весьма большой выборке, оказался равен 0,9. Это говорит о том, что в качестве критерия достаточно использовать лишь один из данных показателей. Естественно, более удобным для расчетов является количество полетов.
Вывозной налет характеризует лишь первый этап в освоении программы летного обучения на данном типе самолета. Для оценки качества летного обучения в целом, в том числе освоения различных видов полетов, этого недостаточно.
Оценка профессиональных способностей по 9-балльной шкале. Ее лучше всего проиллюстрировать на примере оценки летных способностей. Летчиков-инструкторов и командиров знакомят с приводимой ниже шкалой оценок, в соответствии с которой они должны оценить успеваемость каждого курсанта. Непременным условием является соблюдение независимости оценок – командир не должен знать, как оценил данного курсанта другой командир или летчик-инструктор. Уточненная оценка летных способностей по 9-балльной шкале является исходной для выделения ведущего критерия.
9-балльная шкала оценок летных способностей курсантов
9. Очень высокие летные способности. Лучший курсант в части, один из лучших в училище.8. Высокие летные способности. Выделяется среди других по легкости освоения летной профессии. Один из лучших в полку.7. Хорошие летные способности. Быстрее других усваивает технику пилотирования. Один из лучших курсантов в эскадрильи.6. Летные способности выше средних. Несколько лучше, чем большинство других, овладевает летным делом. Один из лучших курсантов звена.5. Средние летные способности. Обычный курсант, ничем особенно не отличается. Быстрота освоения летного дела и качество пилотирования средние. Есть курсанты, успевающие лучше, есть хуже.4. Летные способности ниже средних. Перерывы в полетах, усложнение обстановки, новые задачи сказываются на его успеваемости больше, чем на других. В звене считается слабым курсантом.3. Летные способности низкие. Навыки вырабатываются медленно, требует больше внимания, чем другие курсанты. Один из слабых курсантов в эскадрильи.2. Летные способности очень низкие. Технику пилотирования осваивает медленнее остальных курсантов, летные навыки недостаточно прочные; требует очень много дополнительных вывозных и контрольных полетов. Один из слабых курсантов полка, неперспективный для обучения профессии летчика.1. Летные способности отсутствуют или недостаточны для овладения профессией летчика по профилю училища. Лучше избрать другой вид деятельности. Представляется на отчисление по летной неуспеваемости.
Ранговые порядки учащихся. Путем бесед с преподавателями, инструкторами определяется место в ранговом порядке, занимаемое каждым учащимся в группе, на курсе по качеству освоения программы обучения (не считая отчисленных): Л – лучший, С – средний; Х – худший; Н – неперспективный.
В результате сравнения ранговых порядков в группе, на курсе выводится скорректированная ранговая оценка.
Оценка напряженности учащихся. Инструкторский и преподавательский состав по приводимой ниже схеме оценивает силу и продолжительность, форму и место проявления, внешние признаки напряженности и указывает причину ее появления.
I. Сила и продолжительность: 1) кратковременная, незначительная или средняя; 2) кратковременная, сильно выраженная: а) имела место только в начале обучения; б) систематически вновь повторяется при переходе к новым элементам и видам; 3) длительная, незначительная или средняя; 4) длительная, значительная: а) поддается устранению; б) не поддается устранению.
II. Форма проявления: 1) тормозная – преобладает заторможенность, скованность действий, запоздалые реакции; сужен объем памяти и внимания, медленное переключение и распределение; заторможенность мышления, вычислительных операций, сообразительности; 2) импульсивная – преобладают импульсивные, резкие, размашистые, несоразмерные и некоординированные движения и действия; нарушение дифференцировки поступающих сигналов, забывание порядка действий; взгляд «бегает» по приборам, при ведении радиообмена кричит; 3) генерализованная – резкое ухудшение деятельности обучающихся с одновременным снижением темпа работы и нарастанием ошибок; неспособность целенаправленно сконцентрировать внимание на приборах и органах управления, собраться с мыслями, вспомнить порядок действий; не может разобраться в происходящем.
III. Место проявления (для курсантов-летчиков): 1) перед посадкой в кабину; 2) при запуске двигателя; 3) на максимальных оборотах; 4) на рулении; 5) на взлете; 6) в полете (какой этап); 7) на посадке.
IV. Внешние признаки: 1) вегетативные – повышенный пульс; поверхностное дыхание, непроизвольные задержки его; выраженные изменения кровяного давления; заметное усиление потоотделения; изменение цвета лица и мимики; сухость во рту (изменяется интонация голоса); расширение зрачков; 2) эмоционально-моторные – ухудшение координации и точности движений; «зажим» ручки управления; нарушение дифференцировки усилий; несоразмерность усилий; несоразмерность движений; понижение способности сохранять равновесие или правильное положение тела в кабине самолета; 3) эмоционально-сенсорные – замедленное или ошибочное считывание показаний приборов; нарушение распределения и переключения внимания; «прилипание» внимания; ухудшение восприятия речи и звуков, ведения радиообмена; понижение мышечного и тактильного чувства; 4) эмоционально-интеллектуальные – снижение критичности оценки своих действий; затруднение мыслительных операций; ухудшение памяти вплоть до забывания простейших действий; появление немотивированных действий.
V. Причины: 1) эмоциональная – новизна обстановки; неуверенность в своих силах, знаниях и способности успешно выполнить элемент, фигуру или полет в целом; ожидание сложных элементов или ситуаций; работа в жестком лимите времени; работа в сложном информационном поле; временные неудачи в полете; различные эмоциональные воздействия индивидуального значения; 2) интеллектуальная – низкий уровень общей подготовки и специальных знаний; недостаточная подготовленность к конкретному вылету; 3) психофизиологическая – слабое развитие профессиональных качеств; недостаточное соответствие психофизиологических особенностей личности требованиям летной профессии; воздействия экстремальных факторов деятельности; плохая переносимость деятельности; переутомление, заболевания; 4) методико-педагогическая – постановка непосильных задач; временные неудачи; неучет психологических особенностей учащихся; грубое обращение перед и во время выполнения задачи; 5) мотивационная – нежелание учиться; ошибка в выборе профессии; чрезмерное старание.
Ошибочные действия и предпосылки к профессиональным происшествиям. В процессе беседы с инструктором, а также из документов (например, журнал руководителя полетов, карточка учета и т. д.) выясняется, какое количество ошибочных действий допустил учащийся, их характер, повторяемость, воздействие их на безопасность труда (несущественные, компенсируемые и создающие угрозу выполнению задания).
Отчисления из учебного заведения. Одним из наиболее существенных показателей эффективности профессионального обучения являются случаи отчислений учащихся по «неуспеваемости». Кроме того, мы считаем, что отчисления по «нежеланию», «недисциплинированности», «теоретической неуспеваемости» и в ряде случаев по «медицинскому несоответствию» являются показателями плохой адаптации учащихся к условиям пребывания в вузе и служат косвенными критериями профессиональных способностей.
Дополнительно, для оценки общего уровня развития, специальной подготовки курсанта могут использоваться показатели обучения (оценки по семестрам, курсам, из справки к диплому и др.), по теоретическим дисциплинам и тренажной подготовке.
10.2. Показатели оценки профессиональной пригодности специалистов
Задача определения профессиональной пригодности специалистов более сложна и требует более внимательного подхода. Для правильной оценки профпригодности, например, летчиков необходимо получить и проанализировать такие вопросы, как классность (когда и какой класс получил, его ежегодное подтверждение и при переучивании), освоенные типы самолетов, налет по годам и типам самолетов, продвижение по «служебной лестнице», ошибочные действия и предпосылки, характеристики командования (независимые характеристики, оценка по 9-балльной шкале) и др.
Кроме изучения документов, характеризующих профессиональную подготовку летчиков по указанным выше критериям, с командирами проводится краткая целенаправленная беседа анкетного характера: 1) испытывал ли он затруднения при вводе летчика в строй в части после окончания училища (по сравнению с другими молодыми летчиками)? 2) к какой группе летчик относится: лучше всех; входит в число лучших; на уровне обычных летчиков; несколько слабее других; самый слабый? 3) какое место летчик занимает отдельно по летным способностям и деловым и психолого-педагогическим качествам? 4) какой должности по своим летным и деловым качествам будет соответствовать данный летчик через 10–15 лет?
После ответа на вопросы (в анкету могут быть включены и другие вопросы) командирам предлагается оценить профессиональную деятельность летчика в соответствии с 9-балльной шкалой оценок (приводится ниже). Каждый из них должен оценить летчиков по данной шкале конкретным баллом. При этом необходимо соблюдать условие, чтобы каждый командир давал оценку самостоятельно, не зная оценок других. Разъясняя командирам цель сбора этих сведений и их неофициальный характер, следует подчеркнуть, что эти критерии будут использованы исключительно в научных исследованиях. Строгое соблюдение этих условий, а также необычность системы оценок позволяют получить достоверную информацию.
9-балльная шкала оценок профессиональной деятельности летчика
Отличный летчик
9. Блестящие летные способности. Выдающийся воздушный ас, непобедимый в бою. Лучший летчик части или даже соединения.
8. Очень высокие летные способности. Талантливый летчик, намного выделяющийся среди остальных, даже более опытных. Один из лучших летчиков части.
7. Высокие летные способности. Отличный летчик, быстрее своих товарищей по возрасту (летному стажу) овладевающий летным мастерством. Один из лучших летчиков части.
Хороший летчик
6. Хорошие летные способности. Перспективный летчик, среди таких же, как он, по возрасту Является одним из лучших по технике пилотирования.5. Хорошие летные способности. Обычный хороший летчик, ничем особенно не выделяющийся. По технике пилотирования средний среди летчиков того же возраста.4. Средние летные способности. В обычных условиях хороший летчик, однако перерывы в полетах, усложнение обстановки снижают его работоспособность заметнее, чем у других.Средний летчик
3. Средние летные способности. Неплохой летчик, однако профессиональные навыки недостаточно прочны. Требует больше внимания, чем большинство летчиков того же возраста.2. Летные способности ниже средних. Овладевает летной профессией медленнее, чем другие летчики.Слабый (неперспективный) летчик
1. Недостаточные летные способности. В полетах допускает много ошибок. Было бы лучше, если бы он не поступал в летное училище, а избрал другую профессию.
10.3. Приемы оценки прогностической ценности методик
Прогностическая ценность (информативность, прогностичность) как отдельных методик, так и интегрального показателя профессиональной пригодности может определяться в зависимости от целей выявления профпригодности (отбор, подбор, экспертиза и т. д.) по одному из критериев профессиональной успеваемости, эффективности реальной деятельности, по их совокупности или по ведущему критерию (по оценке профессиональных способностей).
При сопоставлении указанных параметров большое значение имеет выбор соответствующих математико-статистических моделей оценки различий и связи между признаками. В практике психологического отбора летчиков себя оправдали такие методы, как анализ альтернативных признаков, критерии величины и достоверности различий, корреляционный анализ и др.
Основные критерии, по которым можно проводить сравнение результатов экспериментально-психологического обследования с успешностью летного обучения и деятельности для определения прогностической валидности методик психологического отбора, приведены в таблице 2.
Анализ альтернативных признаков. Определяя основные показатели профпригодности и успешности профессионального обучения, приходится иметь дело с изменчивостью качественных признаков, которые в вариационные ряды не распределяются, а рассматриваются как противопоставляемые друг другу состояния. Например, из 700 кандидатов в IV группу психологического отбора вошло 50 человек. Анализируя данные, мы противопоставляем эту группу оставшимся 650 кандидатам. В такой альтернативной форме могут рассматриваться как качественные, так и количественные признаки сравниваемых явлений.
Таблица 2.
Основные показатели оценки результатов экспериментально-психологического обследования и профессиональной деятельности
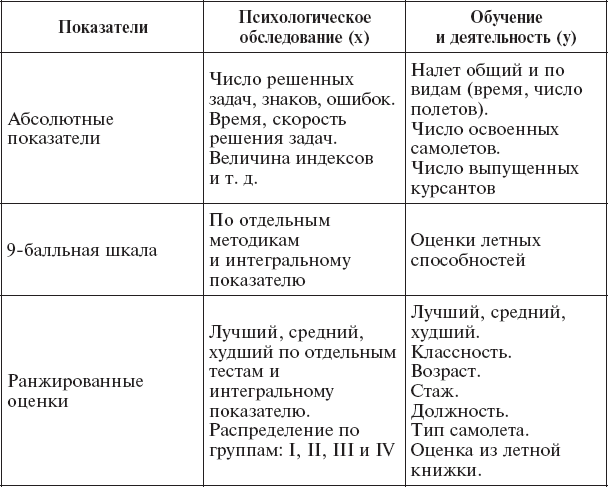
Альтернативные признаки выражаются в абсолютных значениях частот, с которыми они встречаются в данной совокупности, а также в долях единицы или в процентах от общего числа наблюдений. Например, в отношении обследованных 700 кандидатов можно сказать, что среди них IV группа составляет 7 %.
Основным альтернативным признаком для оценки эффективности психологического отбора в целом следует считать относительное распределение по группам и баллам учащихся, отчисленных по различным причинам и отдельно по профессиональной неуспеваемости (табл. 3).
Таблица 3
Количество курсантов, отчисленных по летной неуспеваемости, по группам, по 9-балльной шкале психологического отбора и курсам обучения

Аналогично можно проанализировать другие причины отчислений из училища (теоретическая неуспеваемость, медицинское несоответствие, нежелание учиться, недисциплинированность).
Прогностическая эффективность отдельных методик и интегрального показателя психологического отбора могут быть также определены по формуле:
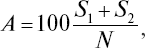
где А – общий процент оправдавшихся прогнозов; S1, S2 – число положительных и отрицательных прогнозов, которые оправдались; N – общее число кандидатов.
Критерии, по которым оценивается эффективность психологического отбора в отношении успешности освоения программы профессионального обучения (исключая отчисленных), приведены в таблице 4.
Таблица 4
Распределение средних величин ранговых порядков, оценок летных способностей, числа полетов по группам, 9-балльной шкале психологического отбора и курсам обучения (1–4)
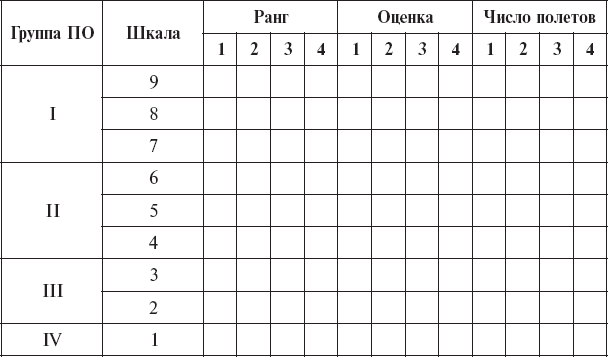
Имея ранжированные критерии успешности летного обучения (оценка летных способностей по 9-балльной шкале и ранговые порядки), необходимо через них проанализировать прогностичность критериев психологического отбора (табл. 5).
Для правильной оценки полученных средних величин критериев психологического отбора при сопоставлении их с критериями успешности обучения необходимым является определение величины и достоверности различных сравниваемых параметров.
Критерии величины и достоверности различий. Прогностическая валидность методик в зависимости от характеристик оценок используемых внешних критериев и теста может определяться также путем выделения из всего контингента двух групп: а) заведомо хороших специалистов (лучших); б) бесспорно плохих (худших) или отчисленных по неспособности к обучению. Результаты психологического обследования по методике или интегральному показателю этих групп составляют два вариационных ряда, и по различиям между ними определяется прогностическая валидность. Если ряды окажутся статистически неразличимы, то данная методика не содержит сведений для дифференциальной диагностики пригодных и непригодных специалистов, то есть ее информативность мала. Чем больше степень различия, тем выше информативность методики. Сравнение вариационных рядов можно проводить с помощью различных методов.
Таблица 5
Распределение средних величин результатов психологического отбора по 9-балльной шкале летных способностей и ранговым порядкам при освоении учебного (учебно-боевого) самолета
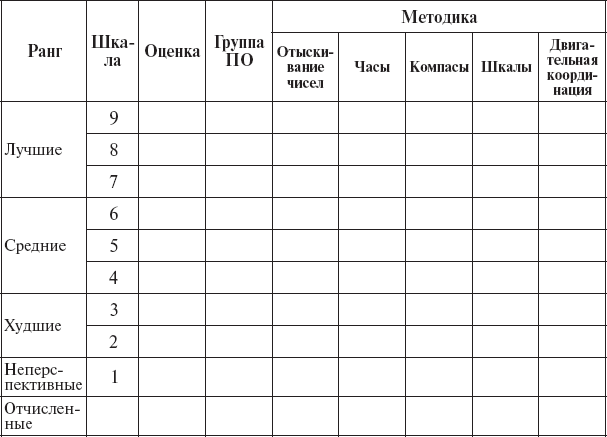
В большинстве случаев, когда распределение вариант в изучаемых совокупностях достаточно близко к нормальному виду, для сравнения средних значений применяется критерий Стьюдента (1), являющийся величиной безразмерной.
Уровень значимости различий P между сравниваемыми средними находится по t в специальной таблице. P зависит от числа степеней свободы (К) или объема выборки (N) и величины t. В практике статистической обработки результатов исследований принято использовать три уровня значимости: P1 = 95 %, P2 = 99 %, P3 = 99,9 %. Величина уровня значимости устанавливается самим исследователем в зависимости от степени точности, с какой проводится исследование, и ответственности выводов, вытекающих из него. Обычно уровень значимости различий между сравниваемыми параметрами, равный 95 %, считается достаточно надежным. Однако в тех случаях, когда на основании проведенных исследований делаются широкие обобщения и выводы особенно строгие, принимаются (99 %) и 99,9 %-ные уровни. Например, когда исследователь приходит к выводу о необходимости включения новой методики в комплекс имеющихся тестов или о нецелесообразности приема для обучения определенной категории кандидатов в связи с высоким процентом отчислений и большими денежными затратами на их подготовку, то уровень значимости, конечно, должен быть очень высоким.
В случаях, когда необходимо проверить гипотезу при небольшой выборке и отсутствии нормального распределения, проверка значимости различий между сравниваемыми параметрами может быть осуществлена с помощью критериев, не требующих трудоемкого вычисления каких-либо статистических параметров, то есть непараметрических критериев различия. Кроме того, они весьма удобны для анализа таких исследований, где сравниваемые показатели выражаются не в конкретных (абсолютных) мерах измерения (количество полетов, время и т. п.), а шкалами порядка, баллами или рангами по изучаемому признаку.
Учитывая, что все методики и интегральный показатель психологического отбора, а также основные критерии успешности профессионального (летного) обучения выражаются именно в баллах и рангах, использование непараметрических критериев должно найти широкое применение.
Применяя непараметрические критерии различий, необходимо вначале использовать менее мощные (критерий Вилкоксона и критерий Розенбаума), но и менее трудоемкие, а при получении сомнительных результатов применить более мощные (критерии Ван дер Вардена, Колмогорова – Смирнова).
Для определения различий при помощи критерия Вилкоксона [141] следует расположить все данные в один упорядоченный ряд и проставить их ранги (R). Например, необходимо сравнить результаты психологического отбора по методике «Шкалы» у лучших (x) и худших (y) по летной подготовке на учебном самолете – соответственно 9 и 9 курсантов.
Располагаем баллы лучших и худших в упорядоченные ряды:
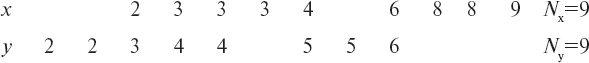
Далее, упорядоченные ряды необходимо проранжировать и подсчитать сумму рангов для каждого из рядов:
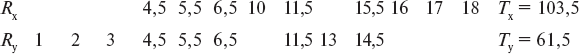
После подсчета находим в специальной таблице на пересечении Nx и Ny критическое значение T, которое сравнивается с меньшей из суммы Tx и Ty, и определяется уровень достоверности различий. В случае, когда меньшая из сумм превосходит критическое значение T, разница между сравниваемыми параметрами считается недостоверной или, наоборот, достоверной на 95 %-ном или более уровне значимости.
В разбираемом случае критическое значение T для Nx = 9 и Ny = 10 на уровне достоверности различий в 95 % равно 64, а в 99 % – 58. Анализируя прогностичность методики «Шкалы», можно отметить, что критическое значение T больше суммы Ty (меньшая из двух); 65 больше 61,5, а это свидетельствует о достоверности различий между лучшими и худшими по летной подготовке на уровне 95 % в выполнении ими данного теста.
Параметрические и непараметрические критерии можно использовать при определении достоверности различий между группами психологического отбора, интегральным баллом, баллами по отдельным методикам, с одной стороны, а с другой – различными категориями отчисленных студентов (курсантов), баллами профессиональных способностей, рангами, числом полетов, то есть практически между всеми критериями психологического отбора и успешности обучения.
Корреляционный анализ. При изучении взаимосвязи критериев психологического отбора с успешностью обучения и профессиональной деятельности можно заметить, что изменения первого признака соответствуют изменениям второго. В некоторых случаях зависимость проявляется очень сильно, однако такие однозначные или функциональные связи встречаются редко, особенно в психологических исследованиях, где числовой характеристике теста может соответствовать не одно определенное значение критерия профессиональной деятельности, а целый ряд их варьирующих значений.
В большинстве психолого-педагогических исследований связь между результатами обследования и успешностью обучения довольно часто и сильно нарушается различными привходящими факторами, поэтому она не всегда может быть четко установлена. В таких случаях зависимость между изучаемыми критериями носит характер, при котором каждому значению одной из переменных соответствует не какое-то конкретное значение, а определенная групповая средняя другой переменной.
Такая связь называется корреляционной (корреляция), а математический анализ связей, существующий между ними, составляет содержание корреляционного анализа.
В задачи корреляционного анализа при определении прогностической валидности методик входит измерение тесноты или степени сопряженности между варьирующими признаками, ее направления и формы, а также последующая оценка достоверности полученных показателей связи.
Корреляционную связь между изучаемыми признаками можно обнаружить с помощью ряда показателей. Решению вопроса о выборе наиболее адекватного метода помогает предварительное расположение в определенном порядке двух сопряженных рядов, позволяющее судить о наличии или отсутствии связи между ними. Более информативным является составление корреляционных матриц и графиков регрессии, дающих наглядное представление о форме и направлении корреляции, а также ее динамике.
При выборе того или иного показателя необходимо учесть, по каким признакам проводится корреляционный анализ (качественным или количественным), форму корреляционной зависимости (линейная или нелинейная) и возможность группирования изучаемых величин в вариационные ряды. Следует помнить, что корреляционный анализ служит инструментом только количественного выражения связей между варьирующими признаками и позволяет оценить достоверность корреляции. Поэтому, несмотря на большую ценность этого метода, его не следует переоценивать, а тем более подменять им профессиональный и психолого-педагогический анализ факторов.
При изучении связи между критериями психологического отбора и успешностью летного обучения целесообразно построение «корреляционной решетки» (табл. 6).
Таблица 6
Образец построения корреляционной решетки для 9-балльной шкалы

Частота вариант сопряженных видов – Pxy, занимая в таблице определенное положение, позволяет судить о наличии и направлении и частично о тесноте связи между баллами психологического отбора и баллами успешности летного обучения (варьирующими признаками) – x и y.
Если частоты Pxy располагаются преимущественно по диагонали с левого верхнего угла решетки к правому нижнему, как показано в нашем примере, – это указывает на положительную связь между признаками. При отсутствии корреляционной связи частоты распределяются по клеткам корреляционной решетки равномерно. О наличии отрицательной связи свидетельствует распределение частот в направлении от верхнего правого к нижнему левому углу. Это правомерно для тех случаев, когда баллы (классовые варианты) располагаются по возрастанию или убыванию (однонаправленно) слева направо сверху вниз.
После предварительного изучения (по характеру распределения частот в корреляционной решетке) тесноты и направления связи при определении необходимости дальнейшего анализа вычисляется коэффициент корреляции (r).
При изучении корреляции между критериями, выраженными в абсолютных величинах и с небольшим количеством сопоставляемых пар, техника вычисления r довольно проста. Например, необходимо изучить связь между результатами выполнения методики «Часы» (число ошибок) – x и количеством полетов на учебно-боевом самолете – y (табл. 7).
Для вычисления коэффициента корреляции необходимо еще определить величину дисперсии – С для x, y, d по формуле
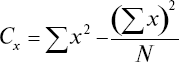
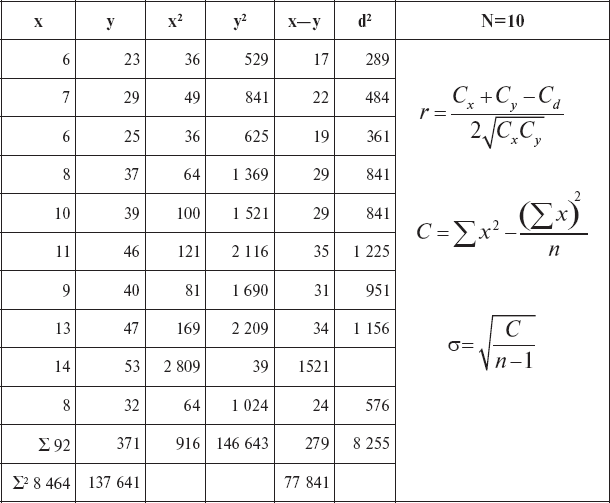
Подставляя значения из таблицы в формулу, находим: Cx = 69,6; Cy = 878,9; Cd = 470,9; r = 0,965. Устанавливаем достоверность полученного коэффициента корреляции:
Таблица 7
Вычисление коэффициента корреляции
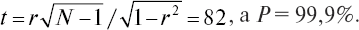
В данном случае коэффициент корреляции можно было вычислить не по абсолютным (числовым) значениям признаков, а по соответствующим рангам, которые имеет каждый курсант. Такой анализ взаимосвязи называется «показатель корреляции рангов» (табл. 8).
Показатель корреляции рангов несколько отличается от коэффициента корреляции, так как ранги не могут точно соответствовать равностоящим значениям количественных величин. Учитывая, что неточность не превышает нескольких процентов, а вычисление показателя корреляции рангов значительно проще, он может служить приближенной оценкой коэффициента корреляции.
При изучении корреляционной зависимости между критериями, выраженными в баллах или классовых вариантах и при большом количестве сопоставляемых пар, целесообразней r вычислять по способу сумм [141] с использованием корреляционной решетки и формулы
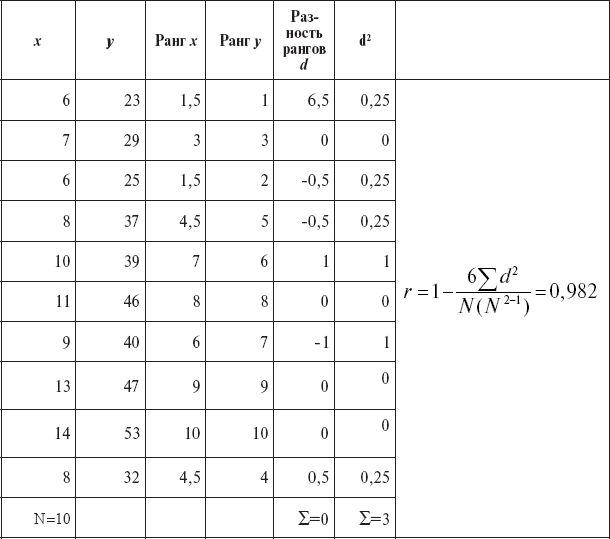
Таблица 8
Расчет показателя корреляции рангов
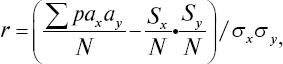
где Spaxay – сумма произведений частот корреляционной решетки (Pxy) на соответствующие порядковые номера классов (баллов); S – сумма первого полного ряда накопленных частот, получаемого кумуляцией частот каждого ряда в направлении, обратном порядковой нумерации классов; σx и σy – средние квадратические отклонения рядов; N – общее число парных наблюдений.
Изучая корреляционную связь между двумя признаками x и y, необходимо помнить о возможности существования зависимости или влияния на них других варьирующих признаков. Поэтому наряду с изучением парных корреляций возникает задача измерения множественных связей между варьирующими признаками индивидуальных психофизиологических особенностей организма и критериями успешности обучения. Для решения этой задачи необходимо воспользоваться коэффициентом общей или совокупной корреляции и частными или парциальными коэффициентами корреляции.
Совокупный коэффициент корреляции между варьирующими признаками x, y и z вычисляется по следующей формуле:
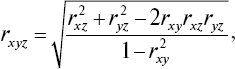
где rxy, rxz и ryz – парные коэффициенты линейной корреляции между признаками x и y, x и z, y и z.
На практике чаще применяется парциальный коэффициент корреляции, измеряющий связь между двумя варьирующими признаками x и y при постоянном значении третьего – z – учитываемого признака, который может иметь или имеет связь с первыми двумя. Так, парциальный коэффициент между x и y при исключительном влиянии на эту связь, составляет
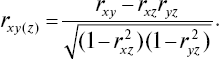
Соответственно рассчитываются коэффициенты парциальной корреляции между x и z при влиянии y– rxz(y); y и z – при влиянии x– ryz(x).
Как видно из приведенных формул, расчет значений совокупного и парциальных коэффициентов корреляций производится на основе парных коэффициентов корреляций.
В некоторых случаях возникает необходимость изучения связи между несколькими внешними критериями, даваемыми разными экспертами (независимые характеристики, ранжирование и др.), и ее достоверности. Например, для обеспечения объективности выведения оценки летных способностей курсантов по 9-балльной шкале по мнению четырех экспертов А, Б, В, Г из летно-инструкторского состава (командир и его заместители) необходимо определить степень совпадения их мнений в отношении одних и тех же курсантов. Для этой цели используется показатель корреляции рангов для суммарной ранжировки – коэффициент конкордации
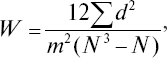
где Σd2 – сумма квадратов отклонений индивидуальных сумм рангов от средней индивидуальной суммы рангов; m – число сравниваемых ранжированных рядов; N – численность выборки. W показывает степень согласия ранжированных рядов, и его значения могут колебаться от 0 до 1 (табл. 9).
В данном примере он достаточно высок (W = 0,91) и свидетельствует о единстве мнений внешних экспертов по оценке летных способностей курсантов.
В ряде случаев, когда критерии профессионально-психологической пригодности и успешности обучения не распределяются в вариационный ряд, корреляция между ними устанавливается по наличию нескольких качественных признаков в связи с качественными признаками обучения.
Корреляция между качественными признаками, группируемыми в 4-клеточную корреляционную решетку, определяется c помощью коэффициента ассоциации (ra) Дж. Юла – тетрахорического показателя связи. Когда изучается корреляционная зависимость между несколькими качественными признаками, группируемыми в многоклеточные таблицы, используется коэффициент взаимной сопряженности (К) – полихорический показатель связи.
Таблица 9
Расчет коэффициента конкордации
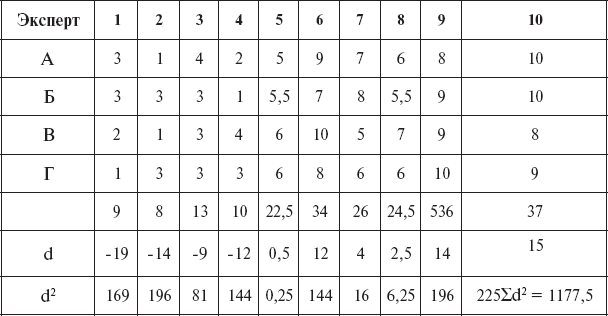
Таблица 10
Расчет коэффициента ассоциации
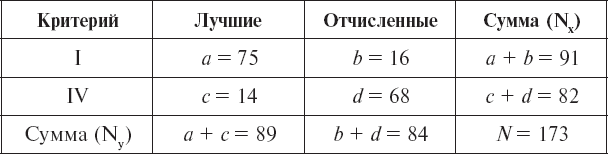
Рассмотрим пример вычисления коэффициента ассоциации при изучении связи между такими критериями пригодности, как I и IV группы, и критериями успешности обучения – лучшие и отчисленные:
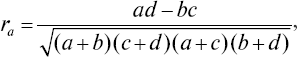
где a, b, c, d – численности альтернативных признаков (практически неограничены).
В корреляционной решетке (табл. 10) приведены исходные данные для расчетов (x – группа; y – успешность обучения).
Подставляя в формулу соответствующие значения из таблицы, находим величину коэффициента ассоциации (ra = 0,65), который выражается в долях от 0 до 1. Достоверность оценивается по его отношению к средней ошибке, определяемой по формуле
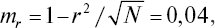
откуда t = 16,25.
Достоверность ra может быть определена также и по специальным таблицам [52].
При изучении корреляционной зависимости между вариационными рядами с отсутствием линейной зависимости более правомерным является вычисление корреляционного отношения, которое измеряет состояние любых, в том числе и нелинейных, связей между признаками.
В отличие от коэффициента корреляции, изучающего двустороннюю связь между x и y, корреляционное отношение (η) показывает только зависимость изменений второго (y) признака от изменений первого (x), или наоборот. Корреляционное отношение – величина относительная, положительная и принимает значение от 0 до 1. Показатели корреляционного отношения обычно не равны между собой – ηy/x ≠ ηx/y. Они определяются по следующим формулам
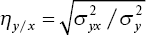
и
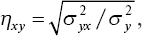
где

Эти формулы можно выразить и в другом виде:
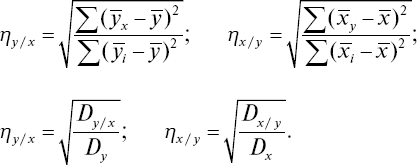
По приведенным формулам удобно определять коэффициенты корреляционного отношения для небольших выборок, а при наличии большого числа наблюдений необходимо предварительно весь материал группировать в вариационные ряды и вносить в корреляционную таблицу.
Рассмотрим вычисление корреляционного отношения на выборке из 10 наблюдений (табл. 11).
Таблица 11
Вычисление корреляционного отношения
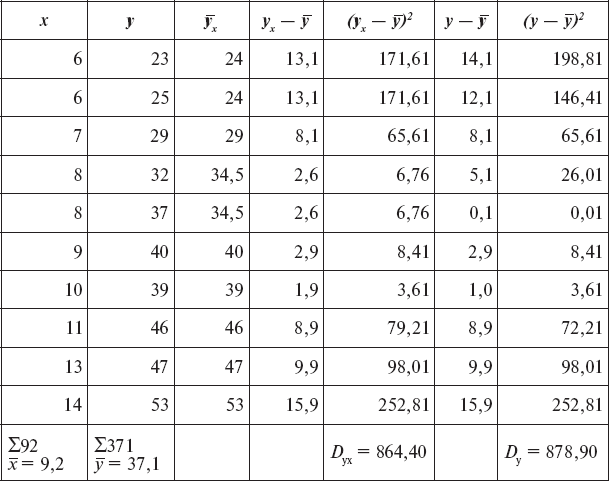
Сначала находим коэффициент корреляционного отношения полетов y по грубым ошибкам x, то есть ηy/x, для чего ранжируем выборку по x (значения x расположены в возрастающем порядке сверху вниз). Затем определяем вспомогательные величины для вычисления корреляционного отношения по x и подставляем в формулу, откуда ηy/x = 0,99.
Таким же способном определяем корреляционные отношения грубых ошибок x по полетам y, ранжируя выборку по y и определяем ηy/x.
Для оценки достоверности полученных величин используем формулу
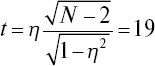
и по специальной таблице [52] находим значение P = 99,9 %.
Вычисление корреляционного отношения на больших выборках после предварительного заполнения корреляционной решетки можно производить по способу произведений, способу условных средних и способу суммирования [141].
Регрессионный анализ. Описанные показатели корреляции позволяют измерять степень связи, направление и форму существующей между ними зависимости. Однако они не дают информации о том, насколько в среднем может измениться в ту или другую сторону один из признаков при изменении другого. Такая информация представляет большой практический интерес для разработки методик психологического отбора, а также изучения влияния специальных методов подготовки на успешность профессионального обучения.
Функция, позволяющая по величине одного признака (x) находить средние (ожидаемые) значения другого признака 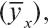 связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.
связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.
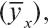 связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.
связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.Важную роль в регрессионном анализе играет коэффициент регрессии (R), являющийся не только параметром уравнения, но и мерой регрессии y по x и x по y. Показатели его величины (n) характеризуют зависимость между переменными x и y по их абсолютным значениям, а показатели корреляции – величины относительные и измеряют тесноту связи между признаками в долях единицы. Коэффициент регрессии характеризует только линейную связь, при которой увеличения (уменьшения) одной переменной – y– пропорциональны увеличениям другой – x, и в зависимости от направления связь либо положительна, либо отрицательна. По значениям R легко определяется коэффициент корреляции 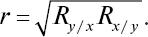 Зависимость между R и rпозволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.
Зависимость между R и rпозволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.
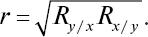 Зависимость между R и rпозволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.
Зависимость между R и rпозволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.Коэффициент регрессии позволяет рассчитать, насколько в среднем изменится признак при изменении на единицу меры другого связанного с ним признака. Он рассчитывается по коэффициентам корреляции и средним квадратическим отклонениям сопряженных видов по следующим формулам:
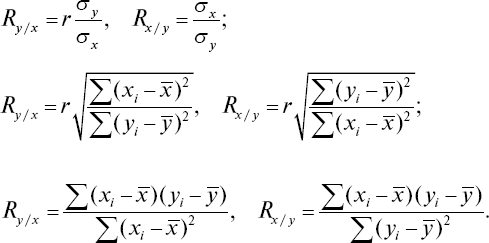
По формулам Ry/x определяется среднее (ожидаемое) значение y при изменении на единицу меры х, а по формулам Rx/y находят среднюю величину х при изменении на единицу меры признака у.
Имея возможность легко менять условия проведения эксперимента по методике у и быстро оценивать полученные результаты, мы можем установить необходимые или оптимальные условия для другой методики x – более сложной и трудоемкой. Зная интеркорреляционные связи между методиками «батареи» тестов и проводя регрессионный анализ, можно добиться оптимальных и наиболее целесообразных условий их проведения и соответственно повысить прогностичность «батареи» в целом. Например, коэффициент корреляции между результатами обследования по методике y (время – с.) и x (количество ошибок) равен +0,25; σy = 27, σx = 5. Подставляя значения в формулу, находим Ry/x = 1,35 и Rx/y = 0,995. Это означает, что увеличение времени выполнения на 1 сек соответствует увеличению количества ошибок в среднем на 0,05 ошибок, а увеличение на одну ошибку при выполнении задания соответствует увеличению времени чтения таблицы на 1,35 с.
Если сравнивать время чтения и количество ошибок по отношениям между средними арифметическими величинами этих признаков (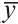 = 242,
= 242, 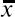 = 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку – 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии y по x и x по y. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.
= 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку – 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии y по x и x по y. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.
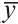 = 242,
= 242, 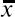 = 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку – 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии y по x и x по y. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.
= 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку – 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии y по x и x по y. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.Достоверность коэффициента регрессии, как и любого другого выборочного показателя, оценивается по критерию Стьюдента с числом степеней свободы K = N–2. В обоих случаях ty/x и tx/y коэффициенты регрессии достоверны на 99,9 %-ном уровне.
Для прогнозирования успешности обучения и реальной деятельности (по результатам психологического обследования) может быть использован аппарат регрессионного и последовательно-дискриминантного анализа. А. Н. Лебедев разработал компьютерные программы факторного, кластерного и регрессионного анализа, которые использовались для распознавания внешнего критерия эффективности службы в системе органов внутренних дел [196].
Мерой связи между внешним критерием (например, фактором «профессионализм») и тестовым показателем служит коэффициент линейной корреляции по Пирсону. Коэффициент принимает значения от –1 до +1. Показатели связаны положительно, если с ростом одного из них возрастает и второй, и, наоборот, при росте одного и уменьшении другого. Коэффициенты корреляции рассчитываются для выборки в целом. Однако интерес представляет конкретный человек, у которого по показателям психодиагностических измерений можно было бы предсказать профессиональную успешность. Для этого используется техника регрессионного анализа.
В простейшем случае, если обозначить буквой «Д» прогнозируемую оценку профессиональной успешности конкретного человека, а «Х» – его тестовый показатель, то прогноз можно определить по формуле:
Д = r × Х,
где r – коэффициент корреляции.
От относительных величин (нормированных) легко перейти к абсолютным. В этом случае формула регрессии принимает вид:
Д = А + кХ,
где Д и Х – нормированные показатели; А – свободный член; к – коэффициент при аргументе, то есть тестовом показателе.
Полностью поведение человека непредсказуемо, и коэффициент корреляции между внешним (рабочим) поведением и результатами отдельных тестовых измерений, как правило, составляет 0,2–0,3. Однако множество разных тестовых показателей, взятых в совокупности, связаны с прогнозируемым поведенческим качеством сильнее. Происходит совокупное усиление возможностей в задаче распознавания внешнего «образа».
Для прогноза в этом случае используется уравнение множественной регрессии типа:
Д = А + R Х1 + m • X2 + i • X3 + … + q • Xn,
где Д – прогнозируемая поведенческая величина (например, уровень «профессионализма»), R, m, i, q – коэффициенты уравнения, полученные ранее на большой выборке испытуемых; X1, X2, X3 … Xn – показатели тестовых измерений.
Для получения коэффициентов диагностических уравнений множественной регрессии иногда используют не всю выборку, а только полярные группы, то есть самых успешных профессионалов и тех, от которых целесообразно избавиться.
Разработанный методический подход, по мнению Б. Г. Бовина, имеет свои преимущества и недостатки [196]. Положительными качествами являются, в частности, быстрота расчета и эффективность оценивания информативности применяемых методов. Одновременно можно использовать практически любое количество показателей, из которых автоматизированная процедура позволяет сделать выбор тех, которые имеют отношение к распознаванию заданного «образа». Заданным «образом» может быть любой внешний критерий: наиболее и наименее профессионально успешные сотрудники, студенты с разным уровнем академической успеваемости, виновники аварийных ситуаций и т. п.
Другим преимуществом является достаточно полная картина статистических характеристик, получаемых на промежуточном этапе, которые позволяют исследовать многочисленные связи между используемыми параметрами. Различные психодиагностические методы могут сравниваться по тому вкладу, который они вносят в распознавание заданного «образа». В этом случае можно проверять валидность любых тестов, использование которых дает цифровой показатель.
Последнее преимущество имеет и свой недостаток – происходит определенное «выхолащивание» качественного, содержательного аспекта диагностики. Другим недостатком является нестабильность получаемых моделей распознавания. Каждая новая выборка дает новую модель распознавания неизменного внешнего критерия. В эту модель могут войти другие показатели, ранее отвергнутые в ходе регрессионной процедуры. Это создает ощущение определенной ненадежности полученных результатов. Однако эта неопределенность объясняется тем, что различные показатели обусловлены одним и тем же фактором, то есть несмотря на многовариативность моделей, содержательная сущность их сохраняется.
10.4. Математические процедуры разработки шкал методик
Результаты обследования (абсолютные показатели) по всем методикам, используемым при психологическом отборе, выражаются в оценках (относительных величинах) по 9-балльной шкале. Перевод абсолютных величин результатов обследований в относительные (баллы) может быть осуществлен путем расчета средних арифметических величин и сигмы или путем процентного распределения согласно закону «нормальной кривой» применительно к 9-балльной шкале.
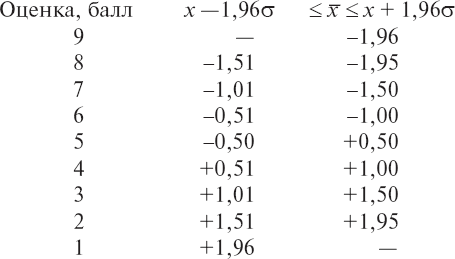
Для середины 9-балльной шкалы (5 баллов) берется интервал, включающий в себя варианты, отстоящие от средней величины на ±0,50 s. Каждый последующий балл в обе стороны от балла 5 составляет интервал в 0,5 s. Такое построение 9-балльной шкалы справедливо, когда число наблюдений (N) превышает 120. При меньшем количестве наблюдений и другом выбранном уровне значимости доверительный интервал определяется по стандартным значениям критерия Стьюдента из специальных таблиц.
Рассчитанная таким образом шкала требует дополнительной корректировки в процессе обследования, так как не дает плавного распределения всего массива результатов. Сама же корректировка проводится опытным путем, что снижает объективность и точность получаемых шкал. Кроме того, расчет s – довольно трудоемкий процесс.
В настоящее время доказано [18, 66], что распределение оценок многих стандартизированных психологических тестов апроксимируется формой «нормальной кривой». Поэтому представляется целесообразным расчет шкал для методики психологического отбора проводить с использованием закона нормального распределения случайных величин.
Расчет шкал с использованием закона нормального распределения случайных величин применительно к 9-балльной шкале оценок производится следующим образом: из всего массива абсолютных показателей сначала выделяется 4 % лучших и 4 % худших показателей, и всем вариантам, начиная с худшего в первом случае и лучшего во втором, соответственно присваиваются баллы 9 и 1; далее из оставшихся снова выделяется, но уже 7 % лучших и худших результатов, и всем вариантам в этих пределах соответственно присваиваются баллы 8, 2 и т. д.
Для того чтобы разработанная шкала отвечала научным требованиям, число наблюдений, на которых она разработана, должно быть 500 и более, так как только в этом случае закон нормального распределения случайных величин (показателей изучения психологических качеств) вступает в силу и будут учтены (оценены) все возможные варианты в пределах указанных процентов применительно к 9-балльной шкале.
Таблица 12
Распределение процентов «нормальной кривой» по группам и баллам интегральной оценки психологического отбора

Корректировка процентов по соответствующим баллам для интегральной оценки и групп психологического отбора проводится на основе экспериментальных исследований и определяется потребностями практики распределения (дифференцировки) кандидатов по результатам психологического отбора (табл. 12).
За абсолютный показатель при выведении интегральной оценки или группы берется сумма баллов (L) по всем методикам с учетом их весовых коэффициентов или коэффициентов корреляции с интегральным внешним критерием. Расчет шкалы производится, как указано выше, аналогично расчету для отдельной методики:
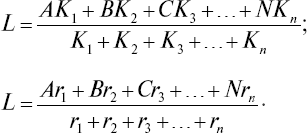
Нормативные оценки по 9-балльной шкале для некоторых методик психологического отбора летчиков по абсолютным показателям приведены в таблице 13.
При разработке шкал как отдельных методик, так и интегрального показателя возникает вопрос определения достаточного объема наблюдений для получения достоверных статистических показателей. Для этого на основе предварительных исследований определяется среднее квадратическое отклонение (s), ориентировочно характеризующее колеблемость изучаемого признака в генеральной совокупности. Далее устанавливается необходимый уровень доверительной вероятности (P), который определяется целями исследования и соответствует значениям:
Таблица 13
Нормативные оценки методик психологического отбора
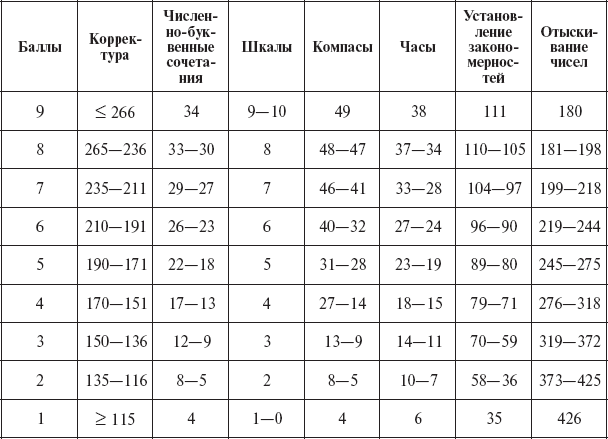
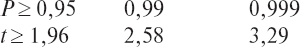
Наконец, задается (произвольно, на основании опыта) степень точности (D) характеристики среднего значения генеральной совокупности (допускаемая ошибка отклонения от генеральной совокупности). Расчет необходимой выборки производится по формуле
N = t 2 σ2/Δ2.
Например, необходимо установить N при разработке шкалы конкретной методики. По предварительным расчетам σ = 23, уровень доверительности вероятности P = 0,99 и соответственно t = 2,58, а допускаемая ошибка Δ = 3 с. Подставляя значения в формулу, находим N = 352.
Увеличение или уменьшение выборки произойдет при установлении другого доверительного уровня или точности характеристики среднего значения (допускаемой ошибки). Например, при P = 0,999 количество наблюдений N = 580 и т. д.
Величину допускаемой ошибки можно определить и по формуле
Δ = 2tσ/nk,
где n – размерность используемой шкалы; k – градация абсолютных показателей внутри каждого из 9 баллов; цифра 2 введена для учета знаков «минус» и «плюс». При определении максимально допустимого значения ошибки k не учитывается. Для более точного определения Δ градация внутри каждого балла k должна составлять 3,5 или более вариантов. Например, величина ошибки для 9-балльной шкалы методики при P = 0,99 и σ = 23 и трех вариантов значений абсолютных показателей внутри каждого балла (3 с) будет составлять: Δ = 4,4 с, а максимально допустимая величина Δ = 13 с, то есть без градаций внутри каждого балла. При изменении доверительной вероятности и градаций внутри баллов будет меняться и Δ.
Правильность (не валидность) построения методик может быть проверена путем изучения фактического распределения абсолютных показателей в процентах по соответствующим баллам 9-балльной шкалы. Так, если фактическое распределение совпадает с расчетным, методика составлена правильно. Если произошел сдвиг в сторону 1 или 9 баллов, то это означает, что степень трудности, условия или время предъявления подобраны неправильно и этот недостаток необходимо устранить. Например, при выполнении методики «Часы» результаты обследования распределились по 9-балльной шкале со сдвигом к 9 баллам по отношению к расчетным. Это означает, что время на выполнение задания (12 мин) велико и большее, чем должно быть, число испытуемых успевают правильно решить все задачи. Уменьшение времени выполнения до 8 мин привело к нормальному (расчетному) распределению полученных результатов.
Для определения правильности выбора единиц измерения или градаций методики можно воспользоваться формулой Δ = 2tσ/nk. В тех случаях, когда Δ составляет часть от неделимой единицы измерения, эта единица измерения не может быть использована в качестве дифференциации данного текста. Например, в методике «Компасы» единицей измерения является задача из одного компаса, то есть он может быть учтен или нет. Эта единица измерения неделима, часть компаса не может быть учтена. Полученная часть единицы дает сведения о том, на сколько нужно увеличить (расширить) количество задач или как изменить единицу измерения. Так, например, если Δ оказалась равной 1,3 – это значит, что количество задач в тесте должно быть увеличено в 3 или более раза. С увеличением числа задач в тесте этот недостаток устраняется. Практические исследования показывают, что количество задач в тесте должно быть (при P = 0,95 и максимально допустимом значении Δ) не менее 20.
В. С. Аванесов [5] приводит примерные числа высказываний для разработки вопросников: минимальное число – 10; достаточное – от 23 до 29; практически оптимальное – от 30 до 40; теоретически желаемое – свыше 41.
10.5. Статистический алгоритм разделения субъектов на классы профессиональной пригодности
10.5.1. Постановка задачи
Пусть информация о психологических особенностях человека содержится в n-мерном векторе v (v1, v2, …, vn). Каждое из vj (i = 1, 2, …, n) – число, полученное при помощи той или другой методики (среди них могут быть определенным образом закодированы и качественные характеристики человека). В дальнейшем компоненты v будут называться признаками. Выбор признаков обычно производится с учетом психологических требований к профессиональной пригодности. Предлагаемый алгоритм позволяет отбросить те из используемых признаков, которые оказываются неинформативными для данной конкретной задачи определения профессиональной пригодности.
Предполагается, что группам лиц, с одной стороны, пригодных (группа «А»), а с другой стороны, непригодных (группа «В») к рассматриваемой деятельности соответствуют два класса n-мерных векторов {vA} и {vB}, которые могут сильно пересекаться, но статистически различны. В дальнейшем всегда будем считать, что {vA} – класс векторов, характеризующих пригодных к данной деятельности субъектов.
С математической точки зрения задача определения профессиональной пригодности заключается в отнесении с определенной вероятностью ошибки вектора (v1, v2, …, vn) к одному из двух классов – «А» или «В».
Имеется много различных методов решения этой задачи. Во всех методах необходим этап «обучения»: статистический анализ уже имеющегося опыта. Для целей определения профессиональной пригодности они не получили большого распространения – одни из-за крайней громоздкости и сложности применения даже при помощи вычислительных машин, другие потому, что оказались не очень эффективными.
Успех классификации по многим признакам в задачах диагностики зависит от информативности этих признаков и способа интеграции информации. Этот способ интеграции должен быть:
1) простым в вычислительном отношении и доступным при использовании;
2) малочувствительным к отсутствию какого-либо признака;
3) в какой-то мере инвариантным к сдвигу распределений признаков (последнее существенно в силу необходимости считаться с разными методическими условиями получения одного и того же признака).
Этим требованиям в значительной степени удовлетворяет алгоритм, основанный на модификации последовательного статистического анализа отношения вероятностей [58]. Он был предложен для диагностических целей и оказался весьма эффективным при дифференциальной диагностике ряда заболеваний по таким признакам, на основании которых постановка диагноза оказывалась затрудненной даже для опытных специалистов [63].
Для целей определения профессиональной пригодности этот алгоритм должен быть еще более эффективным, так как психологические признаки v1, v2, …, vn являются слабо статистически зависимыми, а при этих условиях последовательный анализ отношения вероятностей является оптимальной процедурой для классификации на два класса [64].
10.5.2. Алгоритм
Алгоритм состоит из двух этапов: первого – этапа обучения, во время которого накапливается информация о признаках на основании уже имеющегося опыта и оценивается информативность выбранных признаков, и второго – этапа классификации, на котором выносится решение о пригодности субъекта к определенной деятельности.
Обучение. Предполагается, что на основании предыдущего опыта можно выделить группы субъектов «А» и «В», которые отражают наше понимание пригодности (или непригодности) к данной деятельности и являются определенными эталонами для дальнейшего прогнозирования пригодности. Ряд практических вопросов, связанных с образованием классов «А» и «В», будет рассмотрен ниже. Далее предполагается, что имеется какой-то набор признаков v1, v2,…, vn, существенность которых для определения профессиональной пригодности можно и не знать. Теперь можно построить множество векторов {vA} и {vB}, соответственно характеризующих группы субъектов «А» и «В».
Процесс обучения состоит в получении оценки дискретных одномерных распределений вероятностей признаков v1, v2,…, vn для класса «А»: fA1(v1), fA2(v1),…, fAn(v1) для класса «В»: fB1(v1), fB2(v1),…, fBn(v1).
Предполагается, что v1, v2,…, vn слабо зависимы. Если, однако, этого нет, то для увеличения эффективности процедуры в рассмотрение вводятся сложные признаки – синдромы, определение которых можно получить на основании опыта и теоретических соображений или же используя соответствующий математический аппарат. Построение одномерных распределений существенно облегчает процесс обучения, а в случае слабой зависимости потери информации при этом невелики.
Если классы «А» и «В» многочисленны, то можно получить достаточно хорошую оценку требуемых вероятностей {fА(vj)} и {fB(vj)} (i = 1, 2, …, n).
В тех же случаях, когда численности классов «А» и «В» невелики, приходится прибегать к грубому квантованию признаков на 2–3–4 градации. Практическая проверка показывает, что при наличии в группе 25–30 человек и соответствующем квантовании можно получить удовлетворительные результаты.
Полученные в результате обследования данного контингента лиц показатели могут иметь различную ценность для целей прогнозирования профессиональной пригодности. Поэтому следующим этапом «обучения» является оценка информативности признаков.
Признак будет тем более информативным, чем больше различие между его распределениями у представителей класса «А» и «В». Оценка информативности признака v1 может выражаться величиной Pj – вероятностью того, что распределения fАj(vj) и fBj(vj) различны. Это достигается при помощи вычисления χ2. Интуитивно ясно, что вероятность Pj может быть хорошей мерой информативности признака vj при данной конкретной классификации. Необходимо отметить, что признаки, информативные в одном случае, могут оказаться совсем не информативными для решения задачи профотбора других специалистов.
Вычисление c2 производилось по формуле:
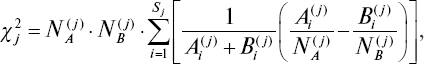
где NA(j) и NB(j)– общее число лиц соответственно в классах «А» и «В», данные которых использовались при построении распределений для j-го признака;Ai(j) и Bi(j) – частоты появления индивидов в i-й градации j-го признака для сравниваемых классов; Sj – число градаций для j-го признака.
Вероятности Pj определялись по таблицам Л. Большова и Н. Смирнова [52]. Оценка информативности может быть также получена и при помощи расстояния Кульбака. В принятых здесь обозначениях и несколько измененной форме это расстояние имеет вид:
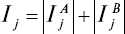
где
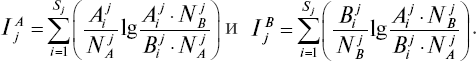
Эта мера имеет ряд преимуществ, особенно при теоретических исследований. Для практики представляет интерес возможность измерения значимости признаков v1(j = 1, 2, …, n) отдельно для вынесения решения о принадлежности v к {vA} или {vB} (соответственно слагаемые IAj и IBj ).
Используя ту или другую меру, признаки целесообразно расположить по их убывающей информативности, а те из них, которые неинформативны (P слишком велико или I – мало), использовать не надо. Если окажется, что информативных признаков осталось мало, то необходимо ввести новые признаки.
Процесс «обучения» можно считать законченным, когда оценки распределений fАj(vj) и fBj(vj) (j = 1, 2, …, n) достаточно надежны, признаки упорядочены по их информативности и их достаточно много.
Классификация (решающее правило). При классификации можно допустить две ошибки. Субъект из класса «А» может быть ошибочно отнесен к классу «В» и, наоборот, субъект из класса «В» может быть ошибочно причислен к классу «А». Первую из указанных ошибок классификации будем обозначать через α, а вторую через β.
Вероятности ошибок α и β определяются до проведения классификации. При выборе этих вероятностей должна быть учтена важность той или другой ошибки классификации, а также реальная ситуация, возникшая при решении данной конкретной задачи.
Пусть при обследовании субъекта S были получены признаки v10, v20,…, Vn0 (они приведены здесь в порядке их убывающей информативности). Пусть на основании здравого смысла выбраны допустимые вероятности ошибок α и β. Рассмотрим отношение вероятностей, соответствующих первому признаку:
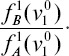
Если это отношение будет меньше, чем
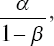
то это будет означать, что полученное значение признака v10 настолько вероятнее для класса «А», что можно с выбранным уровнем надежности (α, β) утверждать, что данное лицо относится к классу «А» (пригодно к данной профессиональной деятельности). Если это отношение
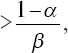
то с тем же уровнем надежности принимается решение о непригодности к рассматриваемой деятельности. Если
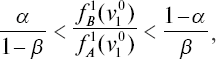
то информация, заключенная в признаке, недостаточна для отнесения к классам «А» и «В» и рассматривается следующий признак v20.
Если
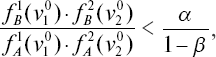
то выносится решение об отнесении индивида в класс «А»; если
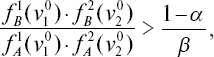
то в класс «В».
Когда же
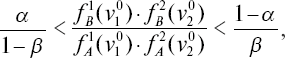
то рассматривается значение третьего признака v30 и т. д.
Если, перебрав все признаки, не удается отнести субъекта к тому или иному классу с данным уровнем надежности, то есть рассматриваемое отношение не выходит за пределы требуемых рубежей, то это означает, что имеющиеся результаты обследования не позволяют сделать прогноз с выбранным уровнем надежности. В этих случаях можно понизить этот уровень и таким образом сделать прогноз или обратиться за дополнительной информацией.
При отсутствии дополнительной информации для минимизации вероятности ошибки целесообразно построить два распределения отношения правдоподобия по всем признакам соответственно для групп «А» и «В» и на основе этих распределений выбрать один порог. Особенности распределения обычно таковы, что этим порогом редко бывает 1.
Как известно, в схемах последовательного статистического анализа [58] процедуры обосновываются для однородного случая, когда fA1(v1) = fA2(v2) =… = fAn(vn) и fB1(v1) = fB2(v2) =… = fBn(vn)
Однако нетрудно показать, что зависимость порогов от вероятности ошибок α и β переносится и на случай неодинаковых распределений, возникающих в диагностической задаче.
Практически удобно иметь дело не с отношениями вероятностей, а с логарифмом этого отношения. Тогда все вычисления сводятся к последовательному сложению.
Итак, определение принадлежности векторов v (v1, v2, …, vn) к множеству {vA} или {vB} осуществляется следующим образом. Последовательно вычисляются величины L1, L2, …, Lk, где
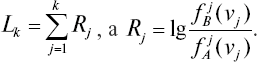
Каждое вычисленное Lk сравнивается с порогами
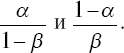
Если при некотором k < n
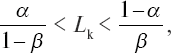
то вычисляется Lk+1. Если же
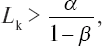
то v ⊂ {vB}; если же
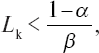
то v ⊂ {vB}.
10.5.3. Градация признаков
При использовании любых количественных методов для отбора приходится прибегать к квантованию признака, так как часто не удается достаточно точно измерить то или другое свойство человека, определяющее его индивидуальные психологические особенности. В таких случаях количество градаций зависит от нашего умения дифференцировать данный признак. Если признак измеряется достаточно точно (например, время реакции), то число градаций можно объективизировать. В данном случае, когда необходимо строить одномерные распределения признаков, число градаций в первую очередь зависит от количества лиц в обучающих группах. Если число лиц достаточно велико, число градаций принимается равным 9–12.
Если же число лиц невелико (25–30 человек), то квантование признака на диапазоны обеспечивается, исходя из особенностей получающихся гистограмм. На основании опыта установлено, что в таких случаях достаточно 2, 3, 4 диапазона. В ряде случаев, когда распределения имеют сложную форму, диапазоны градаций будут неодинаковыми.
Общим правилом здесь может быть указание, предписывающее делать такие диапазоны, при которых расстояние (например, X2) между соответствующими распределениями fA(V) и fB(V) будет наибольшим.
10.5.4. Выбор порога
В последовательной статистической процедуре отношения вероятностей предусматриваются два порога:
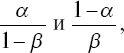
где α, β – ошибки классификации, которые назначаются заранее. Простая зависимость порогов от вероятностей ошибок классификации позволяет выбирать нужный порог, основываясь на сложившейся конъюнктуре.
Необходимость выбора небольшого числа лиц из больших контингентов делает возможным определить a = b порядка 0,001 или даже 0,0001. С другой стороны, при ограниченном количестве лиц естественно выбрать α = β = 0,05 или даже 0,10.
Если окажется, что ошибка пропустить хорошего специалиста и, наоборот, ошибка приема малопригодного неравноценны, то имеется возможность учесть это, выбирая разные вероятности α и β.
Таким образом, выбор порогов является весьма гибким и учитывает реальную обстановку, а также цену возможных ошибок.
10.5.5. Пример
Проиллюстрируем на примере изложенный выше алгоритм определения профессиональной пригодности по психологическим показателям.
Разбиение на классы. В качестве исходного материала для составления дифференциально-диагностической таблицы были использованы результаты психологического обследования двух групп операторов, которых по объективным производственным показателям и характеристикам ведущих специалистов можно отнести к классу «хороших» («А») и «плохих» («В») специалистов.
Представители этих двух классов различались между собой по своей квалификации, а также, частично, по опыту работы.
Операторы, отнесенные к классу «А» (34 человека в возрасте 27–32 лет), прошли длительную подготовку по специальности и имели практический опыт работы в сложных системах управления. Все они характеризовались как специалисты высокой квалификации.
Лица, объединенные в класс «В» (33 человека в возрасте 23–29 лет), имели более низкий уровень подготовки и выполняли операторскую деятельность в менее сложных системах управления.
Психологические показатели. Для оценки состояния ряда психологических качеств и психофизиологических функций был использован комплекс табличных тестов и аппаратурных методик, выбор которых определен требованиями к состоянию ведущих систем организма у данных специалистов. Это:
1. Корректурная проба с кольцами: а) время выполнения задания в сек; б) относительная частота ошибок;
2. «Компасы»: коэффициент успешности;
3. «Отыскивание чисел с переключением»: а) время выполнения задания в сек.; б) производительность – время выполнения одной операции в сек.; в) количество ошибок;
4. «Сложение с переключением»: а) производительность – количество сложений за мин.; б) величина различия в темпе работы; в) относительная частота ошибок;
5. «Перепутанные линии»: а) производительность – количество просмотренных линий за 10 мин.; б) количество ошибок;
6. «Расстановка чисел»: а) производительность; б) относительная частота ошибок;
7. «Память на числа» – воспроизведение сразу после экспозиции: а) коэффициент успешности
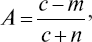
где с – общее число зафиксированных чисел, m – число ошибочно воспроизведенных чисел, n – число невоспроизведенных чисел; б) количество правильно воспроизведенных чисел;
8. «Память на числа» – воспроизведение через 30 мин. после экспозиции: а) коэффициент успешности; б) количество правильно воспроизведенных чисел;
9. «Реакция на движущийся объект»: а) относительная частота точных ответов
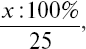
где x – количество точных ответов; б) суммарная величина отклонений от «0»;
10. Тремометрия – проведение стержня в прорези: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;
11. Тремометрия – удержание стержня в отверстии: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;
12. Рефлекс на время – 1 сек.: величина ошибки;
13. Рефлекс на время – 15 сек.: величина ошибки.
Построение распределений. Небольшое число лиц в группах «А» и «В» потребовало проведения грубого квантования, которое был сделано в соответствии с изложенными выше рекомендациями (см. 10.5.3). Диапазоны квантования приведены далее в таблице 15.
Полученные распределения, как правило, существенно отличаются от нормальных, а в ряде случаев имеют U—образную форму (например, показатель относительной частоты ошибок в корректурной пробе). Важно отметить, что для классов «А» и «В», вообще говоря, получены разные по форме распределения одного и того же признака.
Информативность признаков. Оценка признаков проводилась при помощи критерия χ2.
Если Pj > 0,10, то признак считался неинформативным.
В результате анализа было установлено, что некоторые признаки мало информативны для различения классов и могут не рассматриваться. Необходимо отметить, что при других диапазонах квантования информативность признаков может быть несколько другой. Экспериментальное варьирование диапазонов в разумных пределах показало, что получающееся изменение информативности не очень существенно.
Построение диагностической таблицы. Теперь все готово для построения рабочей диагностической таблицы. Для каждого информативного признака вычисляется логарифм отношения вероятностей для значений психофизиологических признаков, попадающих в соответствующие диапазоны, то есть для j-признака и i-диапазона (градации) вычисляются по формуле
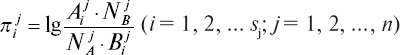
(обозначения определены выше).
Этапы последовательного вычисления диагностических коэффициентов иллюстрируются на примере одного признака (табл. 14).
Таблица 14
Пример вычисления диагностических коэффициентов
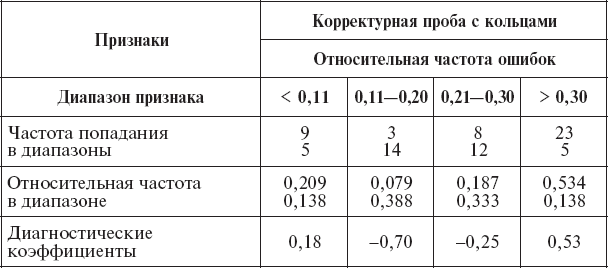
Расположение тех признаков, которые остались после отбраковки, в порядке убывающей информативности с соответствующим «диагностическим коэффициентом», сведены в таблицу 15. В ней заключается вся необходимая информация для проведения классификации на два класса «А» и «В» для новых контингентов людей.
Работа с таблицей и проверка ее эффективности. Пусть допустимые вероятности ошибок классификации a = b = 0,05. Тогда пороговыми значениями будут числа
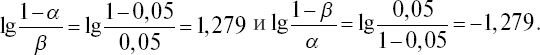
У обследуемого В-ва получены следующие психологические признаки: 1) 0,26; 2) 45; 3) 17; 4) 0,11; 5) 24; 6) 174; 7) 0,14; 8) 1,9; 9) 4,3; 10) 16 и др. (название признаков см. в таблице 15 под теми же номерами)
Находим в таблице 15 соответствующие этим значениям диагностические коэффициенты и последовательно их складываем
(-0,250) + (-0,496) + (-0,449) + (-0,604) + (-0,203)+(0,380)+ (-0,356) + (0,491)+…
Таблица 15
Значения диагностических коэффициентов (пример)
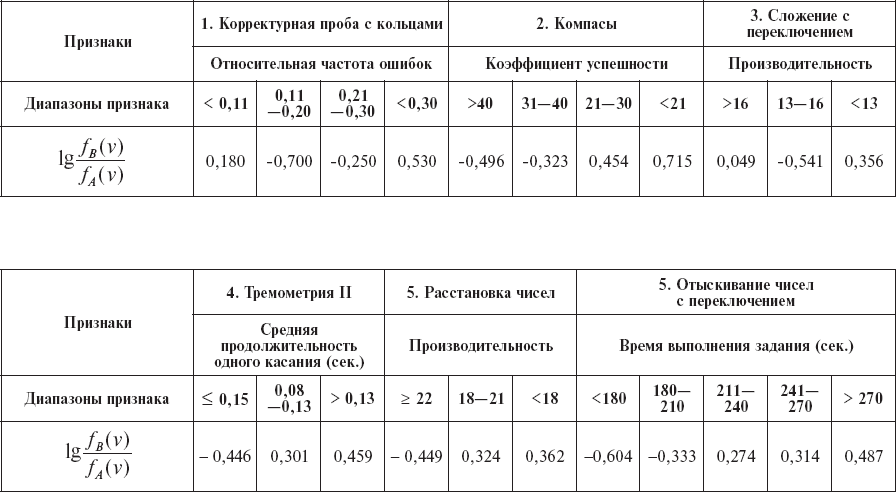
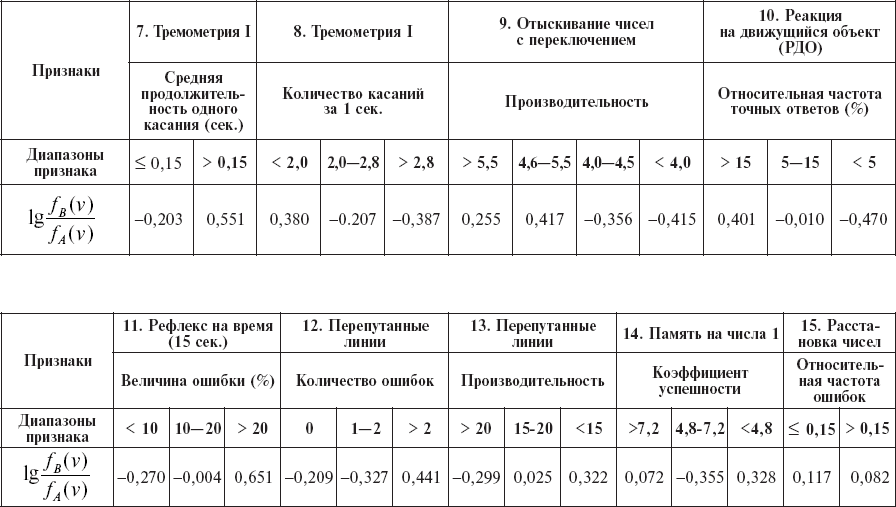
В этом примере оказывается достаточной лишь сумма первых шести признаков, чтобы превысить нижний порог с уровнем надежности P = 0,05.
Таким образом, делается вывод о пригодности обследуемого В-ва к данной операторской деятельности.
Понятно, что эта таблица может быть использована лишь для частного специального случая определения профессиональной пригодности. В других случаях необходимо построение новых подобных таблиц.
Оценку эффективности таких таблиц можно получить, проверив результаты классификации для группы лиц, данные которых послужили основой для ее составления (табл. 16).
Опыт применения классифицирующихся алгоритмов показывает, что результаты различения для проверочной группы оказываются не хуже, чем для группы обучающей [63]. Имелась возможность убедиться в этом при классификации класса «А» на основании данных повторных исследований, сделанных через 30 дней (табл. 17).
Таблица 16
Эффективность диагностической классификации (пример)
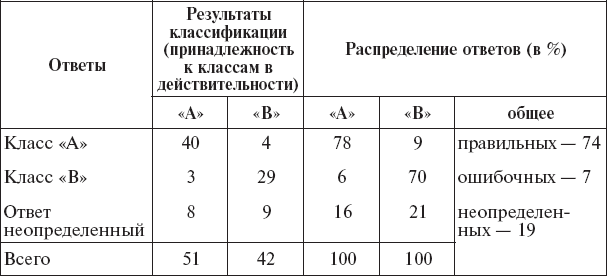
Таблица 17
Результаты повторной оценки эффективности классификации группы «А»
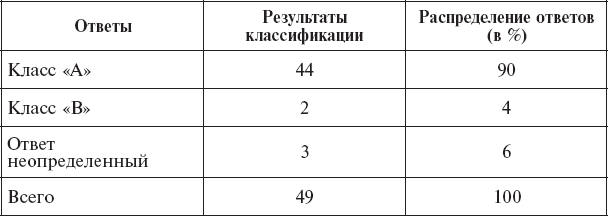
Соответствие ошибок классификации тем, которые были назначены, указывает на то, что в нашем случае статистическая зависимость между признаками мала. И действительно, вычисление интеркорреляций между признаками показало, что в подавляющем числе случаев они оказались статистически независимыми.
Имеются основания считать, что несколько худшие различения класса «В» (см. табл. 17) связаны с наличием большей зависимости между признаками в этом случае.
Таким образом, предлагаемый алгоритм можно рассматривать как реальную основу для решения конкретных задач определения профессиональной пригодности. При использовании простых вычислительных средств оказывается возможным определение наиболее прогностических методик, а после построения таблиц (подобных табл. 14), отнесение данного субъекта с заданной вероятностью ошибки к классу «А» или «В».
Пользоваться такой таблицей удобно – действие сводится к сложению трехзначных чисел. Необходимо подчеркнуть, что последовательный характер вынесения решения позволяет также последовательно получить и психологические характеристики личности, что в большинстве случаев делает излишним проведение полного набора психологических исследований. Кроме того, это также существенно экономит время проведения психологической экспертизы.
Предлагаемый алгоритм имеет определенные преимущества перед другими способами определения профессиональной пригодности не только своей вычислительной простотой и удобством, но и своей эффективностью. Дело в том, что известные математические способы, используемые для целей определения профессиональной пригодности, как правило, предполагают нормальное распределение признаков, что в действительности не имеет места. Эффективность же предлагаемого алгоритма не зависит от вида распределений, а в случае независимости признаков, по-видимому, является и оптимальным методом разделения на два класса.
Уязвимым местом многих статистических алгоритмов является их большая чувствительность к сдвигу центра распределения признаков. Такой сдвиг естественно возникает как результат различных условий проведения тестирующих исследований. Ведь совершенно ясно, что условия получения признаков в обучающих группах и в реальной ситуации могут быть весьма различны. Отношение же вероятностей мало чувствительно к однонаправленному сдвигу центра распределений, и поэтому эффективность неоднородной последовательной статистической процедуры существенно при этом изменяться не будет. Она в какой-то степени инвариантна по отношению к однонаправленному сдвигу центров:
fАj(vj) и fBj(vj) (j = 1, 2, …, n)
В то же время необходимость обучающих групп «А» и «В» является существенным и неустранимым недостатком настоящего алгоритма и может вызвать трудности при решении некоторых задач. Другой недостаток заключается в том, что алгоритм не учитывает зависимость признаков, но этот недостаток может быть устранен при введении сложных признаков – синдромов.
Есть основания считать, что предлагаемый алгоритм будет полезным при решении и ряда других задач, возникающих в прикладной и теоретической психологии. Отметим возможность его применения для тонкой дифференциации психологических состояний на основании наблюдений большого числа признаков, каждый из которых содержит мало информации для различения.
Назад: Глава 9. Методические приемы психологического обследования
Дальше: Раздел III. Результаты экспериментальных исследований и практические рекомендации по определению профессиональной пригодности

