Существует большая разница между тем, как создаются новые идеи и хорошие идеи.

Некоторые определяют ее как различие между правым и левым полушарием мозга. Я бы предложил, как в свое время советовал Дж.-П. Гилфорд, вести речь о конвергентном и дивергентном типах мышления.

Конвергентное мышление – наиболее комфортный из двух типов мышления. Это процесс, о котором мы больше всего читаем в книгах по бизнесу и менеджменту. Это тема семинаров и причина корпоративных перестановок. Конвергентное мышление, как одна часть процесса изменений, принимает идеи и находит им применение.

Дивергентное мышление, с другой стороны, труднее определить. Если схождение (конвергенция) логично (а таковым оно и является), расхождение (дивергенция) магично. Его нельзя организовать, но можно стимулировать.

Табл. 5.1. Конвергентное и дивергентное мышление

Чтобы создать изменения, циклы должны бесконечно чередоваться.

Лучший способ найти хорошую идею – это иметь множество идей.

Но смешивать два этих способа нельзя. Мысль, приведенная к гармонии, сама по себе вредна. Когда мнения совпадают, когда взгляды похожи один на другой, когда различия стираются, когда стандарты унифицируются, а единообразие становится стандартом, изредка случающиеся столкновения идей дают очень мало света. Как и электричество, творческий потенциал есть функция разницы, которая должна поддерживаться между двумя типами мышления: тем, что позволяет изобретать, и тем, что дает возможность оценивать и выносить суждения.

Так что дело в освоении потенциала мышления, которое управляет всеми «за» и, намного позднее, «против», задавая ритм дивергенции и конвергенции, чередуя количество и качество. Изобретательство и критический подход – две разные функции, которые нельзя осуществлять одновременно, даже если время на исходе.

Управление полным циклом мышления, магической его фазой и логической, – задача более сложная, чем те, что привыкли решать лидеры в области политики, бизнеса и профсоюзов. Избыток конвергентного мышления может привести к катастрофе, но то же самое произойдет, если переборщить с дивергентным. Некоторые компании, работавшие в области информационных технологий, канули в Лету, потому что хотели продолжать делать одно и то же, не прислушиваясь к рынку. Другие даже не успели заявить о себе, так и не сумев довести до ума свой продукт, подававший такие надежды!

Если слово «творчество» снова и снова всплывает в их дискуссиях, то почему они не используют методы, которые позволили бы им применить его на практике?

Есть время рассуждать и время действовать. Иными словами, время сомневаться и время принимать решения. И то и другое необходимо и оправдано, но совместить их сложно.

Изменения трудно осуществимы, когда обе операции пытаются проделать одни и те же люди. Можно ли свободно придумать новую структуру, создать новую систему, представить себе новые функции, если знаешь, что предстоит стать частью этой новой структуры, быть вовлеченным в систему или даже исполнять одну из функций? Не будет ли такой человек обречен на муки, как шахматист Стефана Цвейга, который пытается играть сам с собой, сначала с одной стороны, потом – с другой?

Возможно, наши проблемы возникают оттого, что те, кто принимает решения на самом верху, не в состоянии признать важность сомнений, а те, кто способен сомневаться, сами хотят принимать решения. В мире менеджмента препятствием становится многое: мы принимаем желаемое за действительное, вкладываем излишнюю эмоциональность, слышим то, что хотим слышать, и фильтруем информацию.

Демократия также полагается на различные механизмы принятия решений. Каждый должен найти свое место и выполнить свою роль. Платон потерпел поражение, когда в Сиракузах попытался приложить свои концепции к жизни общества. Ньютон, проведший десятки лет в парламенте, выступил там всего один раз, и то лишь затем, чтобы попросить кого-то закрыть окно! Эйнштейн усвоил этот урок и отказался стать президентом только что сформированного государства Израиль.

Неудивительно, что в мире бизнеса мы встречаем столько пар. У них одни и те же ценности, но разные способы мышления. Билл Хьюлетт и Дейв Паккард (HP), Чарльз Роллс и Фредерик Ройс (Rolls-Royce), Гордон Мур и Энди Гроув (Intel), Поль Дюбрюль и Жерар Пелиссон (Accor), Билл Бауэрман и Фил Найт (Nike), Джефф Безос и Джефф Уилк (Amazon), Ларри Пейдж и Сергей Брин (Google). Успех строится на конвергенции и дивергенции.

Творчество – это вопрос гармонии между талантливыми людьми, чередования областей компетентности, пути сообщения между дисциплинами. Короче говоря, это признание незаменимости вклада «Другого». Творческий подход выживет только в том случае, если компании начнут обсуждать идеи.

Если слишком часто случается, что думающие немы, а руководители глухи, это происходит только потому, что отсутствует скрупулезно и симметрично организованное пространство, где уважение к идеям одних соседствует с уважением к ответственности других. Существует множество книг о механизме конвергенции-дивергенции. Я выбрал упражнение, демонстрирующее эту конструкцию и одновременно иллюстрирующее возможность обрести заново творческий подход в информационную эпоху.

Copyгight ©

Задача очень проста (во всяком случае для понимания). Выберите числа из таблицы так, чтобы их сумма равнялась 100:

Скорее всего вам не очень легко даются задачи такого типа. Не сомневайтесь, большинство из нас относятся к ним так же. Но те из вас, кто не сумел ее решить, должны хотя бы задать себе несколько вопросов.

Во-первых, зачем нужна математика? Для того, чтобы справиться с этой задачей, достаточно «азов». Так зачем же она?

А для чего нужна информатика? Представьте, что у вас есть компьютер. Навскидку, что еще может сделать компьютер, кроме того как перепробовать все варианты?

Сколько получается комбинаций? Больше, чем вы думаете. Точнее сказать, два в двенадцатой степени, еще точнее – 4096. Это довольно легко доказать.

Представьте очень простой случай, когда у вас всего три числа. Существует восемь способов выбрать числа. «Ни одного», «все», и еще остается три способа выбрать одно число, и три способа выбрать два; в сумме это дает восемь возможных вариантов.

Табл. 5.2. Убийственные фразы

Это уводит нас на сотни лет назад, потому что цифры (1,3,3,1) взяты из знаменитого треугольника Блеза Паскаля:

Пирамиду можно продолжать до бесконечности, просто складывая два смежных числа, чтобы определить значение того, что под ними. У этого треугольника есть много важных характеристик, но одна из самых интересных для нас – это сумма элементов в строке. Следующее сложение (1,4,6,4,1) дает 16 (два в четвертой степени), и повторение показывает, что сумма каждой строки равна двум в энной степени.

Если вы любитель математики, пролистайте книгу до конца этой главы и полюбуйтесь еще одной знаменитой и прекрасной демонстрацией в решениях к упражнениям.

Так что количество возможностей выбрать числа из дюжины, представленной выше, действительно равно двум в двенадцатой степени (4096).

Их, конечно, можно перепробовать. Однако легко представить, что если бы у нас была, к примеру, сотня чисел, найти ответ таким образом было бы просто немыслимо. Вообще, существует много задач подобного типа. Как распределить частоты для независимых радиостанций, определить, является ли число простым, проверить счета, минимизировать протяженность сети железных дорог – во всех этих случаях метод проб и ошибок настолько же неизбежен, насколько непрактичен.

Одна задача может быть и детской игрушкой, и настоящей головоломкой. Все зависит от размера привходящей информации. Интересная разновидность взаимоотношений, которая заслуживает изучения, – это связь между вычислением необходимого времени и проработанным количеством информации. Возможны практически все сценарии.

Иногда сложность проблемы не зависит от объема информации. Это мечта для пользователя и кошмар для продавца компьютеров, потому что он не может больше увеличивать цену за счет этого! Присвоение новых автомобильных номеров, к примеру, требует усилий, которые ни в коей мере не зависят от количества номеров в пользовании.

Чаще все-таки время расчетов увеличивается пропорционально объему проработанной информации. Это линейная функция, как в случае суммы, где удвоение количества чисел, которые нужно сложить, попросту увеличивает объем работы вдвое.

В большинстве случаев, тем не менее, сложность увеличивается быстрее, чем количество информации, как показано на рис. 5.2. Сортировка миллиона карточек – это намного больший объем работы, чем тысяча отдельных сортировочных процедур для тысячи карточек, и компания, выросшая втрое, должна ввести систему учета, возможно, в десять раз более сложную, чем та, которую она заменила.

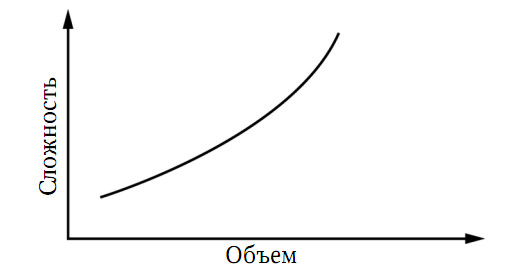
Рис. 5.2. Соотношение объема информации и сложности работы

Практически для всех задач время расчетов увеличивается намного быстрее, чем объем задействованной информации.

Небольшое упражнение, которое мы проделали, наглядно демонстрирует эффект снежного кома. Количество возможных комбинаций взлетает (математики называют это комбинаторным взрывом), и за определенным порогом эта задача превышает возможности даже самых современных компьютеров.

Выражение, которое мы цитировали, можно изменить на «ядерный взрыв» в случае с шахматами, где предвосхищение даже десяти ходов попросту находится за пределами того, что может сегодня информатика.

Вопреки нашим предположениям сегодня пределы расчетов очень редко связаны с трудностью самих расчетов. Чаще они возникают из-за объема информации, которую надо проработать, и необходимости астрономическое количество раз повторить простые расчеты.

И здесь мы должны снова взглянуть на вопрос и обратиться к нашим творческим способностям, которые, если только мы уверены в них, всегда дадут нам преимущество перед любой машиной.

Возвращаясь к начальной задаче – просто измените свое восприятие, подойдите к делу иначе! Попытайтесь увидеть не просто 12 случайных чисел, поищите что-нибудь необычное, какую-нибудь закономерность. Посмотрев на 12 чисел боковым, латеральным, взглядом, убеждаемся, что все они кратны трем, кроме 53 и 17, состоящих из чисел кратных трем плюс 2. Эврика!

Дело в том, что 100 (сумма, которую нам нужно получить) – это число кратное трем плюс 1. Решение, следовательно, обязательно включит в себя 53 и 17. Это единственный способ создать число кратное трем плюс 1, то есть в данном случае 70. Недостающее число (30) получаем как сумму 6+9+15.

Эта задачка из двенадцати чисел была одной из игр, которую стюардессы авиакомпании British Arways подсовывали детям, чтобы на время их утихомирить.

Наше небольшое упражнение также показывает абсолютную необходимость творческого подхода в эпоху информации. Использование латероскопии помогает нам выйти за пределы заданного механизма, потому что момент творчества время от времени прерывает алгоритм. В действительности большой логики в том, что мы внезапно подумали о числах кратных трем не было. Если бы это было логично, мы могли бы запрограммировать компьютер на такие операции. Нас вела уверенность, что дополнительный взгляд на проблему найдет альтернативу «грубой силе», без которой, как казалось на первый взгляд, не обойтись.

Мечта компьютерного ученого состоит в том, чтобы найти для отдельно взятой задачи методику, при которой время расчетов не будет зависеть от объема информации, которую нужно переработать и которая позволит решить систему трех уравнений с тремя неизвестными так же быстро, как и систему из двух уравнений с двумя неизвестными.

Хорошим примером может послужить теннисный турнир, где играют на выбывание. Нам нужно выяснить, сколько состоится игр, включая финал. Представим, что в турнире участвуют 80 игроков, и некоторым из них нужно будет сыграть отборочные игры, чтобы попасть в первый тур. Можно прибегнуть к громоздкому сложению: один финал плюс два полуфинала плюс четыре четверть-финала и так далее, включая отборочные матчи, если количество игроков не равно двум, возведенным в степень. Подойдя к делу творчески, получаем ответ очень быстро. (См. решение в конце главы.)

Творчество в киберпространстве – это рефлекс, который сводится к попытке изменить методы, а не инструментарий.

Творчество в информатике – изменение алгоритма, необходимое, чтобы справиться с большим объемом информации в то же расчетное время. Это рефлекс, предполагающий переосмысливание программ вместо инвестиции в переоборудование.

Космическому зонду Voyager II, запущенному в начале 1970-х годов, потребовалось двенадцать лет, чтобы долететь до Нептуна. Вот пример ускорения маятника. Даже если за эти двенадцать лет население Земли увеличилось бы на миллиард человек, для другого края солнечной системы это незначительный, бесконечно малый срок.

Космический зонд был оборудован бортовым компьютером с 32 КБ памяти! Вся его компьютерная мощность состояла в том, что сегодня может быть доступно в часовом механизме. В NASA была целая команда компьютерных специалистов, основная задача которых состояла в том, чтобы как можно меньше знать, оставаться в стороне от прогресса и не развиваться. Работая без каких бы то ни было новых систем, они в течение долгого времени модифицировали программы летательного аппарата, используя удаленную передачу данных.

Осведомленность, безусловно, является одной из опасностей, присущих технологии. Если бы кому-нибудь пришло в голову спросить сотрудников любого научно-исследовательского центра мира, можно ли отправлять к Нептуну космический корабль со столь крошечной памятью, они почти наверняка ответили бы, что это совершенно невозможно.

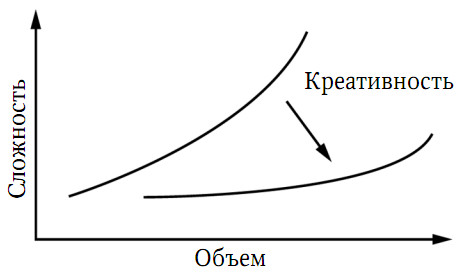
Рис. 5.3. Сложность и творческий подход

Давайте суммируем. Когда требуется решить специфическую задачу, полагайтесь на «магическое мышление». Не бросайтесь сразу в пучину логики. Существует два основополагающих вида суждений: «да, но…» и «да и…». Сказать «да, но…» можно тысячью разных способов – только взгляните на список убийственных фраз из таблицы 5.2 и добавьте свои собственные! Я бы, однако, советовал привыкнуть к «да и.». Это не означает «да», это попросту значит «спасибо». Спасибо за то, что помогли мне выйти за рамки привычного и открыть новую дверь.

Когда я использую упражнение с 12 числами, то через несколько минут кто-нибудь обычно говорит: «Слушай, они же кратны трем!» Кто-то другой тут же добавляет: «Да, но не 17». И они теряют возможность найти решение. Тогда как, сказав: «да и 100 тоже не кратно трем», они могли бы добиться успеха.