Давайте представим как игру отношения двух партнеров: Дона (синий цвет) и Бетти (красный).

Дон и Бетти не относятся к людям с излишне высокими моральными принципами, они не станут переживать из-за собственной измены просто потому что “изменять – плохо”. Вместо этого они предпочтут выйти из игры (из своих отношений с постоянным партнером), набрав как можно больше очков. Результат каждого партнера зависит от избранной им стратегии, что можно изобразить в виде таблицы, которая в математике называется “матрицей выигрышей”:

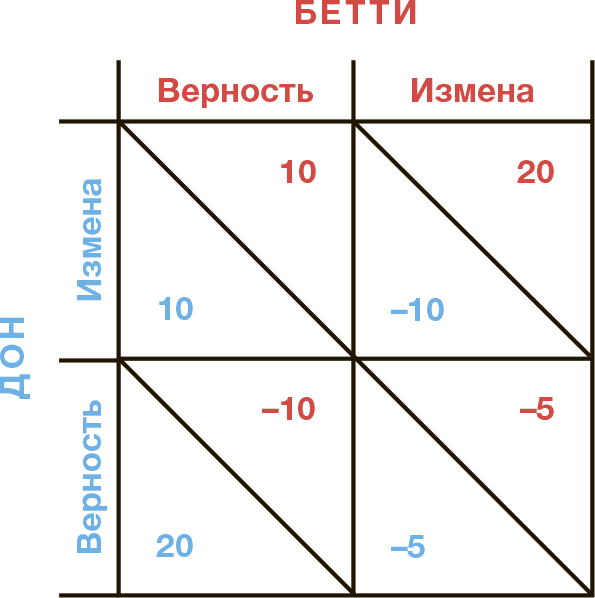
Лучшим вариантом для обоих будет, если Дону и Бетти удастся сохранить верность друг другу. В этом сценарии (который называется “Парето-оптимум”) обе стороны должны остаться в выигрыше, продолжая отношения. Для наглядности давайте представим себе, что в этом случае они оба получают по 10 очков (как мы помним, и Дон, и Бетти хотят в конечном итоге получить как можно больше очков).

Но в этой игре, как и в жизни, всегда будет возникать искушение обмануть партнера (то есть изменить ему). Если Дон решит изменить, он может сохранить свои отношения с Бетти, но при этом заработать “на стороне” 20 очков. При этом Бетти будет травмирована изменой Дона и потеряет 10 очков.

В то же время у самой Бетти примерно такая же ситуация: у нее тоже есть стимул для того, чтобы изменить Дону. Посмотрите, что произойдет, если оба партнера поддадутся искушению и начнут изменять: в этом случае оба проигрывают. Каждый выходит из игры, имея минус 5 очков, отношения разрушены, и оба партнера оказываются в гораздо худшем положении, чем если бы сохраняли верность друг другу.

Цифры в данном примере выбраны произвольно, но нам важно их соотношение: если изменяет только один из партнеров, то он получает больше очков, чем если бы он оставался верен. Но если ваш партнер тоже обманывает вас, то это плохо для вас; и плохо для обоих, если оба партнера обманывают один другого. Применение этих условий превращает игру в верность в эквивалент одной из самых известных и хорошо изученных проблем в теории игр – в “дилемму заключенного”.

Эта дилемма состоит в следующем: двух заключенных порознь допрашивают об одном и том же преступлении. У каждого из них есть два варианта: не выдавать друг друга (то есть молчать) – и тогда они получат одинаковые, сравнительно небольшие сроки – или заговорить и выдать товарища. В последнем случае заговоривший предатель может выйти на свободу – но только при условии, что его подельник продолжает молчать. Если же заговорят оба, то оба получают длительные сроки. Структура выигрыша здесь такая же, как и в игре в верность: давать показания, если другой молчит, выгоднее, чем молчать обоим, а это, в свою очередь, выгоднее, чем взаимное предательство. Для каждого из игроков хуже всего, когда он сам молчит, а партнер его предает.

Конечно, такой подход приводит к довольно депрессивному взгляду на отношения. Получается, что подлинного сотрудничества трудно добиться и еще труднее его поддерживать. И если теория верна, то возможны ли вообще счастье и верность в такой нестабильной области, как отношения?

Да, возможны, поскольку отношения – это не вопрос разовых решений. Матрица выигрыша/проигрыша неприменима к отношениям в целом. Ведь вы играете в эту игру изо дня в день, и каждый день решаете, изменять ли партнеру или хранить ему верность. И здесь кроется ключевое различие. В ходе регулярной игры с одним и тем же партнером расклад меняется. Внезапно вы обнаруживаете, что хотите набрать больше очков в сумме игр, а не в каждой игре по отдельности. Получается, что в долгосрочной перспективе вам обоим выгоднее хранить верность друг другу!