1.7. Медлер и лорд Кельвин

О, эти бездны, влекущие нас ввысь!
Станислав Ежи Лец

Иоганн Генрих Медлер и Уильям Томсон (лорд Кельвин) были первыми профессиональными учеными, предложившими корректное решение фотометрического парадокса.

Немецкий астроном Иоганн Медлер вырос в Берлине. В 19 лет он потерял обоих родителей и был вынужден взять на себя заботу о трех младших сестрах. Медлер стал преподавать в семинарии, давать частные уроки и одновременно посещать занятия в Берлинском университете. В 1824 году он начал читать лекции по астрономии и по математике богатому банкиру Вильгельму Беру, встреча с которым изменила всю жизнь Иоганна. Медлер убедил банкира построить небольшую частную обсерваторию, на которой они с Бером, начиная с 1830 года, стали активно работать. Основным результатом совместной работы Медлера и Бера стала первая подробная карта Луны «Марра selenographica» (1834 год) и подробный текст к ней (1837 год). Эта работа сделала имя Медлера известным и с 1836 года он становится сотрудником Берлинской обсерватории. В 1840 году, после ухода Василия Струве в Пулковскую обсерваторию, освободилось место директора обсерватории в Дерпте (Тарту, Эстония). Медлер занял этот пост, а также стал профессором Дерптского университета. В 1866 году из-за болезни глаз, сделавшей невозможным проведение наблюдений, Медлер ушел в отставку и вернулся в Германию.

Основные научные результаты Иоганна Медлера связаны с исследованием и картографированием поверхностей Луны и Марса, изучением двойных звезд, собственных движений звезд. Известен предложенный Медлером проект календаря, более точного, чем григорианский (в этом календаре на каждые 128 лет приходится не 32 високосных года, а 31).

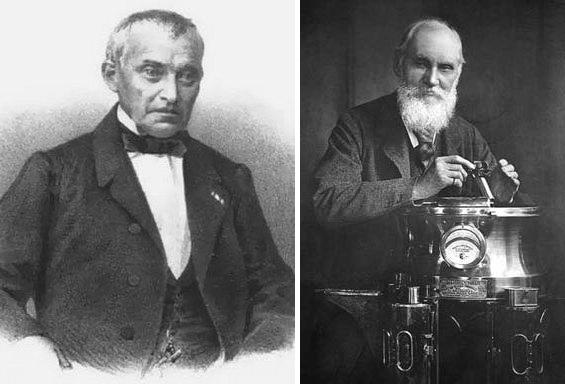
Рис. 13. Иоганн Генрих Медлер (1794–1874) и Уильям Томсон (лорд Кельвин) (1824–1907)

Иоганн Медлер был также очень известным историком и популяризатором астрономии. Его книга «Популярная астрономия», опубликованная в 1841 году и выдержавшая шесть прижизненный изданий, стала знаменитой, ее читали по всему миру. Упоминается в этой книге и фотометрический парадокс, причем разные издания отражают изменение взгляда Медлера на эту проблему. В первых четырех изданиях парадокс обсуждается в терминах поглощения света от далеких звезд. В пятом издании (1861 год) Медлер пишет, что в бесконечной Вселенной, заполненной бесчисленным количеством звезд, все небо должно сиять как Солнце. Этого нет и, следовательно, должно быть расстояние, начиная с которого свет звезд до нас не доходит. Далее, ссылаясь на Ольберса, он упоминает поглощение света, как возможный механизм такой блокировки излучения. Затем следуют слова: «Действительно, такое расстояние существует, но причина совсем в другом. Скорость света конечна; конечное время прошло от начала Творения до наших дней и мы, следовательно, можем наблюдать небесные тела только до расстояния, которое свет прошел в течение этого конечного времени… Вместо того, чтобы говорить, что свет с этих расстояний не дошел до нас, надо говорить, что он еще не дошел до нас».

Приведенные слова Медлера дают четкое решение фотометрического парадокса: Вселенная конечна во времени (но может быть пространственно-бесконечной), скорость света также конечна и, следовательно, начиная с определенного расстояния, равного произведению возраста Вселенной на скорость света, свет более далеких звезд до нас еще не дошел и поэтому ночное небо остается темным.

В XIX веке решение Медлера не привлекло особого внимания. Единственным известным человеком, заметившим его, был Фридрих Энгельс. В своей «Диалектике природы» (1873–82, 1885–86 годы) он написал о приведенных выше словах Медлера как о «великолепном» возражении «против так называемого поглощения света», а предположение, «что только поглощение света способно объяснить темноту заполненного во все стороны на бесконечное расстояние светящимися звездами неба», Энгельс назвал «старомодным взглядом».

В 1895 году, после смерти Энгельса, рукопись «Диалектики природы» попала к его другу – Эдуарду Бернштейну, который ее, однако, не опубликовал. Возможной причиной этого был отзыв Эйнштейна, прочитавшего в 1924 году по просьбе Бернштейна рукопись Энгельса. К идее публикации «Диалектики» Эйнштейн отнесся в целом одобрительно, хотя, по его мнению, она не представляет особого интереса ни для физики, ни для истории физики.

Имя английского физика Уильяма Томсона, более известного как лорд Кельвин, знакомо практически каждому жителю Земли благодаря введенной им абсолютной шкале температуры – шкале Кельвина – и, соответственно, градусам Кельвина. Однако не это сделало его одним из самых выдающихся и авторитетных физиков XIX века. Как писал Эйнштейн, «одаренный богатой фантазией, редким умением применять математический аппарат и проникновенным умом, Томсон около 60 лет участвовал в развитии физики и различных отраслей техники, добыв множество результатов, сохранивших свое значение до сегодняшнего дня; немногие ученые были столь же плодотворны».

Работы Уильяма Томсона относятся к термодинамике, одним из основоположников которой он является, гидродинамике, электромагнетизму, упругости, математике. Очень много сделал Томсон в практической физике и в технике – он изобрел или улучшил множество приборов, вошедших во всеобщее употребление. К концу своей долгой жизни Томсон зарегистрировал 70 патентов и опубликовал более 600 научных работ. За деятельность, связанную с прокладкой трансатлантического кабеля, Уильям Томсон в 1866 году был возведен в дворянское достоинство, а в 1892 году королева Виктория пожаловала ему пэрство с титулом «барон Кельвин».

В 1884 году Уильям Томсон выступил в США с циклом лекций перед избранной аудиторией, состоявшей в основном из американских физиков. Позднее Томсон расширил и дополнил эти лекции, и они были изданы в 1904 году под названием «Балтиморские лекции». Однако еще раньше – в 1901 году – одна из лекций была опубликована как отдельная статья в «Philosophical Magazine». В этой статье Томсон проанализировал фотометрический парадокс в рамках модели свободной от поглощения, однородной статической Вселенной и предложил его первое количественное решение.

Сначала Томсон, используя подход, аналогичный описанному в п. 1.2, оценивает относительную долю небесной сферы α, закрываемую изображениями звезд, равномерно распределенных внутри сферы радиуса r :

где Ν — полное число звезд внутри этой сферы, а a – линейный радиус звезды (все звезды считаются равными Солнцу по светимости и размеру). Далее он отмечает, что эта доля – α – может быть выражена и через отношение яркости покрытого звездами неба I ( sky ) к яркости диска Солнца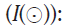

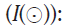
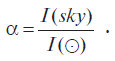
Последняя формула примечательна своей простотой и наглядностью. Из нее сразу следует, что яркость звездного неба (не фона неба, а неба в целом) может быть записана просто как I ( sky ) =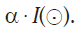

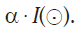Как отметил Эдвард Харрисон, удивительно, что за четыреста лет истории парадокса Кельвин оказался единственным человеком, обратившим внимание на эту простую связь между яркостью звездного неба и долей небосвода, покрываемого изображениями звезд.

Далее Томсон переходит к количественным оценкам. Он берет характеристики нашей звездной системы, примерно соответствующие модели Галактики Вильяма Гершеля, – r = 1000 пк = 3×1016 км, Ν = 109 и а = 7×105 км – и из формулы (3) получает, что α ~ 10-13. Это означает, что яркость неба, определяемая звездами Галактики, какой во времена Томсона ее себе представляли, очень мала и небо должно оставаться темным.

Для того чтобы при сохранении средней пространственной плотности звезд увеличить а, например, до 0.04 (то есть 4 % небесной сферы будет покрыто изображениями звезд), необходимо увеличить радиус звездной системы в 100 миллиардов раз, то есть он должен быть равен 3×1027 км. Свет будет преодолевать это расстояние примерно за 3×1014 лет. Однако, как отмечает Томсон, существуют неоспоримые динамические аргументы в пользу того, что Солнце может существовать как светящийся объект лишь несколько десятков миллионов лет [9] .

Если допустить, что все звезды светят в течение 100 млн лет, то время, в течение которого свет от внешних областей нашей воображаемой сферы добирается до Земли, будет в 3 миллиона раз превышать время жизни звезд. Следовательно, для того чтобы вся небесная сфера была заполнена излучением, необходимо предположить, что приход излучения от звезд, находящихся на разных расстояниях от Земли, синхронизирован – чем дальше от нас звезда, тем раньше она зажглась. Это, конечно, невозможно, поскольку означало бы выделенность положения Земли во Вселенной.

Кроме того, заключает Томсон, предположение о том, что звезды распределены однородно с одинаковой плотностью за пределами нашей звездной системы, конечно, необоснованно. В сфере с радиусом большим, чем наша Галактика, плотность звезд должна быть гораздо меньше и, в итоге, практически нет никакой возможности сделать так, чтобы значение α (то есть величина относительной яркости неба) превышала 10-12 или 10-11.

Таким образом, предложенное Томсоном решение фотометрического парадокса, по сути, состоит в том, что размер наблюдаемой Вселенной гораздо меньше того, который требуется для того, чтобы вся небесная сфера сверкала, как поверхность Солнца. Томсон, по-видимому, считал, что возраст нашей Вселенной ограничен – тогда, естественно, ограничен и размер доступной наблюдениям Вселенной – и поэтому его решение созвучно более ранним идеям Эдгара По и Медлера.

На этом я заканчиваю рассказ об истории фотометрического парадокса в его простейшей формулировке, описанной в начале этой главы. Этот рассказ, естественно, не полон, можно упомянуть еще ряд исследователей, так или иначе затрагивавших парадокс (например, Отто фон Герике, Роберт Гук, Бернар де Фонтенель, Христиан Гюйгенс и др.), однако с основными идеями и с главными действующими лицами в его истории мы уже познакомились. Если бы книга была посвящена только фотометрическому парадоксу, то на этом ее можно было бы закончить. Действительно, наша Вселенная может быть относительно небольшим звездным островком, окруженным со всех сторон темной стеной (так предполагал Кеплер), она может быть конечна во времени и в пространстве (Эдгар По, Медлер, лорд Кельвин) – все эти предположения избавляют нас от парадокса. Однако, конечно, интересно узнать, что на самом деле представляет собой окружающий нас мир и как в реальной Вселенной решается загадка темноты ночного неба. Не менее интересен ответ на этот вопрос в числах – почему ночное небо столь тускло и что из этого следует. Ответам на эти вопросы посвящены две следующие главы книги.

Назад: 1.6. Динамическая Вселенная Эдгара По

Дальше: Глава 2 Как устроена наша Вселенная