Книга: Парадоксы роста. Законы развития человечества
Назад: Что дает модель для понимания истории
Дальше: Литература
Приложение
Математическая теория роста населения Земли
Население мира N (Т) будет описываться функцией от времени Т, определяющей состояние демографической системы Земли. Тогда параметром порядка — ведущей переменной, подчиняющей все остальные переменные, — станет полное число людей N. Таким образом, в этом приближенном функциональном соотношении не учитывается ни распределение населения по нашей планете, ни его экономическое и возрастное состояние или расовый и национальный состав. Сам процесс роста также будет рассматриваться на значительном интервале времени T — большом числе поколений. Иными словами, мы будем рассматривать усредненные значения переменных и усредненные функции. Этим, в частности, вносится в уравнения память о прошлом, определяемая временем усреднения переменных.
Такое выделение главных переменных N и T и их усреднение характерно для системного подхода. Оно получило развитие в синергетике и лежит в основе асимптотических методов, разработанных для решения задач большой сложности, появляющихся при рассмотрении систем со многими степенями свободы. Существенно то, что эти переменные, которые представляют все социально значимые факторы о возрасте и поле, образованию и развитию, доходам и т. д., описываются статистическими распределениями. Поэтому, когда рассматриваются такие многофакторные проблемы, то можно полагать, что в известных пределах развитие системы статистически стационарно и потому происходит динамически самоподобно. Это сильное предположение означает, что остаются неизменными пропорции между относительными изменениями времени и населения.
Смысл этой основной гипотезы автомодельности состоит в том, что утверждается постоянство относительной скорости изменения системы аналогично принципу инерции. В таком случае можно показать, что такой самоподобный рост должен описываться степенной функцией без характерного параметра, такого как масштаб времени. Такие процессы обладают масштабной инвариантностью — скейлингом — аналогично развитой турбулентности в потоке жидкости. Эти понятия мало знакомы историкам и обществоведам, однако они должны помочь в расширении тех образов, которыми мы описываем исторический процесс.
Выше (см. с. 29) изложено, как данные демографии приводят к формуле:
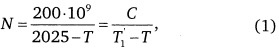
Это выражение как степенная функция обладает масштабной инвариантностью — отсутствием собственного масштаба времени, свойством, открытым еще Эйлером и указывающим на автомодельность роста. В нашей задаче о росте населения эта формула является лишь первым приближением. Как асимптотическое выражение оно ограничено областью применения, и задача теории в первую очередь состоит в установлении этих пределов как вблизи особенности, когда эта функция устремляется в бесконечность, так и в далеком прошлом, когда ее уменьшение происходит слишком медленно. Иными словами, асимптотика ограничена в прошлом нулем и полюсом в настоящее время.
Чтобы описать переход, следует учесть время, характеризующее внутренние процессы, определяемое продолжительностью жизни человека и его репродуктивной деятельности — тех факторов, которые при прохождении через демографический переход ограничивают скорость роста по мере приближения к моменту, когда скорость роста приближается к своему пределу. Для этого следует обратиться к выражению для скорости роста в зависимости от времени, продифференцировав (1):

и затем ввести в это расходящееся выражение характерное время τ, ограничивающее скорость роста:
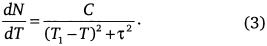
Этот прием может показаться произвольным шагом, однако полученное выражение очень хорошо описывает глобальный демографический переход. Так, мы обратились к методам в теоретической физике, которые развиты для регуляризации расходимости, появившейся при анализе демографического перехода.
Интегрируя (3), получим выражение для описания перехода:
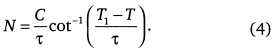
При обращении к последним данным демографии (см. рис. 15) были получены уточненные значения постоянных, что учтено в последующих вычислениях:
С = 163 · 109, Т1 = 1995 г., τ = 45 лет, и безразмерное число К = √C/τ = 60100. (5)
Из-за введения конечного τ полюс в Т1 сдвигается к новому значению Т1 = 1995 г., которое и принято при расчетах, описывающих как демографический переход, так и рост населения мира за пределы Т1 в выражении (4) (см. табл. 1).
В недалеком прошлом выражение (4) асимптотически непосредственно переходит в автомодельный гиперболический рост (1). Однако применительно к очень далекому прошлому скорость роста должна быть ограничена снизу. Этого предположения достаточно для того, чтобы приписать далекому прошлому линейный рост, при котором в первом приближении скорость роста не может быть меньше появления одного гоминида за характерное время τ, пока численность населения не достигает порядка 100 тыс. В популяционной генетике это число К характерно для численности стабильного вида, биологически подобного человеку, и именно с него 1,6 млн лет начинается квадратичный рост, который с тех пор становится доминирующим до эпохи перехода.
Величина К определяет не только масштаб численности человечества в начальную эпоху роста, но и дает оценку численности когерентной группы людей или племени — самодостаточной единицы населения. Как большой параметр задачи постоянная К определяет все соотношения между населением и длительностью процессов роста, а значительная величина константы К приводит к высокой эффективности асимптотических решений. В результате скорость роста населения Земли определяется нелинейным автономным дифференциальным уравнением:

где время t = Т/τ выражено в единицах времени τ, и в решениях уравнения (6) отсчитывается от момента прохождения через демографический переход Т1 Это характерное время одинаково для фазовых переходов в прошлом и настоящем. Сделанные предположения упрощают задачу, сводя все к одной переменной N (Т), рост которой зависит от состояния системы N в момент времени Т. Формула роста (6) выражает природу того коллективного нелинейного взаимодействия, которое ответственно за рост человечества в эпоху его взрывного развития между двумя сингулярностями. В этом уравнении для усредненных переменных T и N скорость роста приравнена к развитию, которое равно квадрату численности населения мира, как выражение меры системной сложности населения планеты.
Население планеты также можно рассматривать как результат парного взаимодействия N человек или как некое эффективное поле, феноменологически определяющее рост. Полное решение должно описывать рост человечества в течение трех эпох. Первая эпоха А — антропогенеза — начинается с линейного роста с указанной выше минимальной скоростью. Когда население достигает величины порядка ста тысяч, наступает эпоха В — взрывного роста — со скоростью роста, пропорциональной квадрату населения Земли. Начиная с этого момента, человек заселяет всю планету.
Когда скорость квадратичного роста достигла своего предела при удвоении за характерное время τ, наступил кризис мирового демографического развития, переход в эпоху С — стабилизации населения мира в рамках приближений теории.
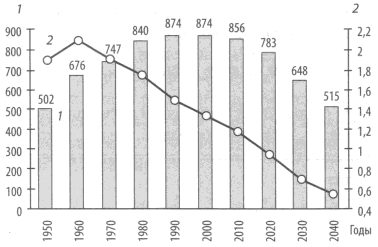
Рис. 18. Мировой демографический переход вблизи 2000 г.
1 — абсолютный прирост населения, усредненный за декаду, млн; 2 — относительный прирост,% в год (данные ООН)
В результате на основании (3) максимальная абсолютная скорость глобального роста во время демографического перехода равна:

при относительном росте:
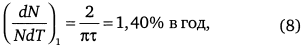
достигнутом в 1995 г., что согласуется с данными ООН, но дает несколько меньшее значение для абсолютной скорости роста при сравнении с табл. 1 (см. рис. 18).
Население нашей планеты в этот критический момент перехода Т1 равно:
N1 = К2/2 = 5680 млн. (9)
На основе этих выражений легко определить предел N∞, в два раза больший, чем N1 к которому в эпоху С асимптотически стремится население Земли:
N∞ = 2N1 = πK2 = 11 360 млн. (10)
В рамках сделанных предположений это число представляет верхнюю оценку населения Земли в предвидимом будущем. Таким образом, глобальное взаимодействие приводит к ускорению и синхронизации процессов и на заключительной стадии демографического перехода — к сужению перехода и тем самым к снижению предела для населения Земли. Этот вывод находится в согласии с эмпирическими наблюдениями демографов. Рассмотрение N (Т) как аналитической функции указывает на асимптотическое поведение при T → ∞, когда N → N∞, в предположении об отсутствии особенностей — полюсов или нулей — в обозримом будущем.
Начальный линейный рост дает оценку времени для эпохи антропогенеза — критической сингулярности в начале предыстории человечества, которая случилась:
T0 - T1 = π/2·Kτ = — τ√πN1/2 = 4,2 млн лет назад, (11)
если использовать известное значение N1 и одно и то же значение τ = 45 лет для сингулярности в далеком прошлом и в настоящем. Несмотря на сделанные упрощения, данная оценка вполне согласуется с оценками времени Т0 в антропологии.
Интересно определить полное число людей, живших на Земле. Если переставить переменные в (6) и проинтегрировать:
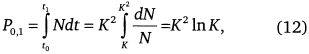
то получим число людей, живших от Т0 до нашего времени Т1 В оценках других авторов длительность поколения принята равной 20 годам, что ведет к оценке Р0,1 = 106 млрд [10]. Поэтому необходимо введение в (12) множителя 45/20 = 2,25:
Р0,1 = 2,25 К2 ln К = 90 млрд. (13)
Таким образом, в течение каждого из ln К = 11,0 выделенных периодов жило по 2,25 K2 = 8 млрд людей. Это число является инвариантным для числа людей, живших в экспоненциально сокращающихся циклах, а ln K указывает на число циклов.
Циклы можно получить, обобщая решение (6) в область комплексных переменных или же просуммировав экспоненциально сокращающиеся циклы:
ΔT = К τ ехр (-θ), (14)
где θ = |ln t| — номер цикла, определить длительность развития при К >> 1:
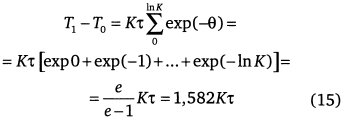
и сравнить ее с (11), где длительность равна Т1 - Т0 = π/2·Kτ = 1,571. В первом случае рост суммируется по гиперболической траектории, во втором — по (4) — N = K tan t/K.
Демографические циклы определяют периодичность развития всего человечества за 4–5 млн лет, включая проходящий по гиперболическому закону рост от конца антропогенеза до наших дней.
Для дальнейшего обзора результатов перейдем к переменной n = N/K:
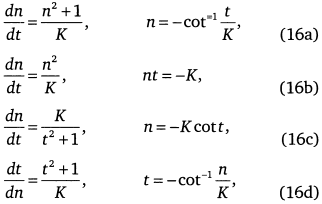
когда мерой численности становится К. Тогда уравнения для роста приобретают симметричный вид и видно сопряжение переменных n и t. Смена зависимой переменной в (16а) и (16d) видна при прохождении перехода, когда n становится независимой переменной вместо времени t, что выражено в уравнении роста (3).
Рост населения можно иллюстрировать геометрическим построением функции тангенса:
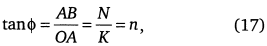
где угол Δφ = τ отображает течение времени, а приращение населения ΔN = 1 (рис. 16).
Линейный рост будет продолжаться до φA,B = Кτ = 1 и NB = tan 1 в точке В на касательной АС. Дальнейший рост N = К(π/2 — φ)-1 будет проходить по гиперболе, при которой время асимптотически стремится к π/2, а население достигнет значения Nc = К2. Когда система приближается к моменту особенности, то от уравнения (16а) следует переходить к уравнению (16d), чтобы описать рост при прохождении особенности в течение эпохи С. Построение показывает, что после перехода от линейного к гиперболическому росту на эпоху В остается в два раза меньше времени, чем на начальную эпоху А. Вывод этого соотношения для всей эпохи В (см. рис. 19) построен при К = 7, когда время от Т0 до Т1 разделено на 11 интервалов, и поскольку к/2 = 1/7, то Nc = К2 =49. Однако даже при таком малом значения К, когда In K = In 1,95 дает хорошую оценку для числа демографических циклов, 1 + In К ≈ 3. Таким образом нулевой цикл антропогенеза продолжался 7 единиц времени, первый цикл длился 3 и последний — одну единицу времени. Это построение показывает, как дискретность времени и населения приводит к появлению периодичности роста, выраженной в демографических циклах как главных эпохах развития человечества.

Рис. 19. Построение функции тангенса, показывающее пределы асимптотик роста
Линейный рост описывает поведение системы вблизи начальной сингулярности роста, начинающейся с N0 = 1 и положительных значений N. Далее следует рост по гиперболе и в конце — сингулярность демографического взрыва. Построение, когда переменные n и t при прохождении перехода меняются местами, мы оставляем читателю.
На рис. 18 показаны функции, описывающие рост системы при К = 1, которые появляются при построении решения, начинающегося с сингулярности в эпоху А, переходящего затем в эпоху В гиперболического роста и завершающегося эпохой С. Асимптотический переход решений, описывающий рост в начале развития и на его конечном участке, получим, обратившись к рядам для функции cot (t/K) и cot-1(t/K):

Эти функции пересекаются в точке А, посередине роста при логарифмическом представлении между временем T0 и T1 соответствующей наступлению неолита:
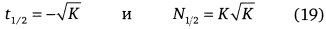
под углом 2/(3K) практически гладко при больших значениях К.
Очевидно, что решение можно строить, отсчитывая время от T0 — от эпохи антропогенеза А при t0 = 0. Тогда, исключив t из (15с), получим одно автономное дифференциальное уравнение, описывающее рост в зависимости от состояния системы, которое определяется населением Земли и где последний член добавлен с тем, чтобы рост в эпоху А никогда не был меньше одного гоминида при Δt = τ.

Интегрируя (20) при значениях K > 1 и начальных условиях t0 = n0 = 0, получим решение:

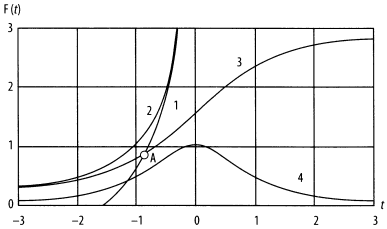
Рис. 20. Функции F (t), описывающие рост

Это решение показывает симметрию переменных N и T — населения и времени. Для развития в течение эпохи В вдали от особенностей роста это выражено в (16в) и следует из сложности причинных связей в рамках развитых представлений о нелинейной динамике глобальной системы населения нашей планеты.
Для того чтобы выяснить устойчивость развития, следует обратиться к уравнению роста человечества (20). На основании (15) в линейном приближении устойчивость роста к возмущениям
δN = δN0 exp(λt) (22)
определит показатель Ляпунова λ развития неустойчивости в системе населения:
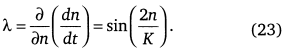
По этому критерию при λ > О движение неустойчиво до перехода. Только после него развитие системы становится асимптотически устойчивым и впредь таким и остается. Отметим, что в этих решениях значение констант роста К и τ не эволюционируют. Более полное определение устойчивости потребует введения распределений для n и обращения к методам статистической физики при обобщении развитой выше модели.
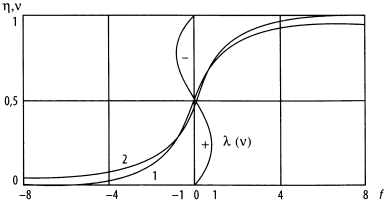
Рис. 21. Переходные процессы и устойчивость роста в линейном приближении
1 — логистический переход ν = 1/1+е-r; 2 — демографический переход η = 1/π соt-1 T и λ (ν).
При гиперболическом росте мгновенное значение экспоненциального роста равно древности,

что и определяет скорость процессов развития в момент времени Т.
В гиперболической хронологии мгновенный экспоненциальный масштаб времени роста линейной неустойчивости по Ляпунову зависит от древности и до демографического перехода равен удвоенному времени роста неустойчивости:
Te = 2τ/λ (25)
Однако наличие выделенных антропологами и историками демографических циклов указывает на глобальную устойчивость с малыми отклонениями системы от предельной траектории роста.
Наконец, из (15) следует, что после каждого цикла до демографического перехода остается приблизительно половина времени длительности цикла:
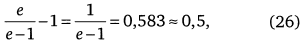
что вполне подтверждается данными истории и антропологии (см. табл. 2, с. 74).
* * *
Асимптотические решения для нелинейных задач приобретают, как заметил Я. Б. Зельдович, то же значение, что частные решения для линейных задач, где действует принцип суперпозиции. В нашей задаче автомодельные решения имеют асимптотический характер, при котором значение некоторых параметров оказываются несущественным, подобно тому как в частных решениях линейных задач происходит вырождение по некоторым параметрам. Так, частота колебаний в линейной задаче не зависит от их амплитуды.
В некоторых случаях независимость от параметра позволяет от уравнений в частных производных перейти к обыкновенным дифференциальным уравнениям. Именно это происходит в задаче о росте человечества, когда в нелинейном уравнении (6) можно пренебречь пространственным распределением населения, поскольку в первом приближении перемещение на конечной по размерам Земле — миграция населения — не влияет на само число людей.
В заключение заметим, что изложенная теория рассматривает задачу о росте и развитии демографической системы в асимптотическом приближении. Из этого следует, что в этом приближении ресурсы не влияют на глобальное взрывное развитие. Поэтому ограничение роста и переход к стабилизации населения мира обязаны внутренним процессам, выраженным в принципе демографического императива, и не подчиняется внешним, в первую очередь ресурсным факторам.
Здесь, несомненно, открывается обширное поле для исследования этой проблемы во всеоружии современных методов статистической физики, теории фазовых переходов и неравновесных систем. Более того, эта задача во многом подобна задачам космологии. Но она гораздо ближе к нам, поскольку имеет огромное значение для фундаментального понимания истории и экономики. Выразим поэтому уверенность, что эта проблематика приведет к развитию своих методов и в теоретической физике.
Назад: Что дает модель для понимания истории
Дальше: Литература

