Пятая глава
Доказывая Калаби

Математическое доказательство чем-то напоминает восхождение на гору. На первом этапе, конечно, требуется найти гору, которая стоила бы восхождения. Представьте себе отдаленную пустынную местность, где еще не ступала нога человека. В наши дни такую местность обнаружить непросто, не говоря уже о том, удастся ли там найти что-то стоящее. Затем альпинист разрабатывает план, как добраться до вершины, который кажется ему безупречным, по крайней мере, на бумаге. После приобретения нужных инструментов и оборудования, а также необходимых навыков, авантюрист приступает к восхождению, однако останавливается, столкнувшись с неожиданными трудностями. Но те, кто пойдет по его следам, используя те из его приемов, которые оказались удачными, выбирая другие пути, — достигнут новых высот на пути к вершине. Наконец появляется некто, не только имеющий хороший план, позволяющий избежать прошлых ошибок, но и решительно настроенный на то, чтобы покорить эту вершину и, возможно, установить на ней флаг в знак своего достижения. В математике угроза жизни и здоровью первопроходцев не столь велика, да и их приключения едва ли покажутся захватывающими кому-либо со стороны. И завершение долгого доказательства ученый не отмечает установкой флага. Он (или она) публикует это доказательство в научном журнале. Или в подстрочном примечании. Или в техническом приложении. В любом случае, и в нашей области есть и азарт, и опасность, с которыми мы постоянно сталкиваемся в процессе поисков, и успех сопутствует тем из нас, кому удалось по-новому взглянуть на скрытые тайны природы.

К началу 1970-х годов уже успело пройти не одно десятилетие с того момента, как Эудженио Калаби обнаружил свою «гору» — впрочем, мы по-прежнему нуждались в подтверждении того, что эта гора действительно была горой, а не, скажем, земляным холмиком. Я, например, вовсе не собирался безоговорочно верить тем неожиданным утверждениям, которые он представил перед нами. Причин для скептицизма, как я уже говорил, было немало. Прежде всего, многие сомневались в возможности существования компактных неограниченных многообразий с нетривиальной риччи-плоской метрикой (отличных от неинтересных нам плоских торов). В то время не было известно ни одного примера подобного многообразия, тогда как этот парень, Калаби, утверждал, что число многообразий данного типа огромно (или даже бесконечно).

Кроме того, Калаби, по словам Роберта Грина, в своей гипотезе воспользовался общим топологическим условием, чтобы получить частный геометрический вывод, который при этом должен быть верен для всего пространства. Для реальных многообразий, у которых отсутствует сложная структура, это неверно, однако для комплексных многообразий, к которым относится гипотеза, это в принципе возможно. Говоря более конкретно, с точки зрения Грина, гипотеза Калаби утверждает, что начиная со случая одного комплексного измерения (и двух вещественных), исходя из общей топологии и формы, где средняя кривизна равна нулю, можно найти метрику или геометрию, где кривизна везде равна нулю. Для случая высоких размерностей гипотеза Калаби конкретно указывает на кривизну Риччи (которая совпадает с гауссовой кривизной для двух вещественных измерений, но отличается от нее, если размерность выше двух), а условие равенства нулю средней кривизны Риччи заменяется условием обращения в нуль первого класса Черна. Калаби утверждал, что если топологическое условие обращения в нуль первого класса Черна выполняется, то должна существовать кэлерова метрика с нулевой кривизной Риччи. Таким образом, весьма широкое и размытое утверждение заменялось гораздо более узким и строгим — и именно поэтому Грин и большинство других математиков сочли это довольно неожиданным.

Я тоже с большим подозрением отнесся к данному утверждению, исходя из ряда формальных причин. Принято было считать, что никто никогда не сможет записать точное решение гипотезы Калаби за исключением разве что нескольких частных случаев. Если это предположение было правильным — что и было впоследствии доказано, — то ситуация становилась безнадежной, и тогда утверждение Калаби можно охарактеризовать как «слишком хорошее, чтобы быть правдой».

Можно провести следующую аналогию с теорией чисел. Хотя существует множество чисел, записать которые на бумаге не составляет ни малейшего труда, существует гораздо более обширный класс чисел, которые мы никогда не сможем записать в явном виде. Эти числа, называемые трансцендентными, включают в свое множество, например, e (2,718…) и π (3,1415…), запись которых даже с триллионом знаков после запятой все равно не будет полной. С технической точки зрения это происходит потому, что такие числа нельзя получить путем алгебраических преобразований и они не являются корнями полинома с рациональными коэффициентами. Ввести их можно только при помощи определенных правил, это означает, что мы можем дать сколь угодно точное и обширное их описание, но никогда — дословное.

Похожая ситуация возникает и с нелинейными уравнениями типа тех, что относятся к гипотезе Калаби. Решением нелинейного уравнения является функция. При этом едва ли стоит ожидать, что найденное решение будет иметь простой и явный вид, например, что его можно будет выразить при помощи точной формулы, поскольку в большинстве случаев таких формул просто не существует. Единственное, что остается, — это пытаться аппроксимировать решение хорошо известными нам функциями: полиномиальными, тригонометрическими (такими, как синус, косинус и тангенс) и некоторыми другими. Если же попытка аппроксимации решения уравнения известными нам функциями оказалась неудачной, у нас начинаются проблемы.

Держа в голове все вышесказанное, я попытался в свободное от работы время найти контрпримеры к гипотезе Калаби. Были волнующие мгновения: мне казалось, что я наконец нашел направление атаки, позволяющее опровергнуть эту гипотезу, — однако позже я обнаруживал изъяны в моей, вроде бы безупречной, конструкции. Это происходило неоднократно. В 1973 году на меня снизошло озарение. На этот раз я чувствовал, что действительно напал на верный путь. Подход, который я избрал — доказательство от противного, — был аналогичен тому подходу, который мы с Ричардом Шоном использовали для доказательства гипотезы о положительности массы. И на этот раз я мог поручиться за безупречность своего доказательства.

Так совпало, что эта идея пришла мне в голову во время международной конференции по геометрии, которая проходила в Стэнфорде в 1973 году, на которой Герох затронул вопрос о гипотезе положительности массы. Принято считать, что конференции — это отличный способ оставаться в курсе событий, как в своей, так и в смежных и даже очень далеких областях исследований, и эта конференция не была исключением. Она стала для меня прекрасным местом для обмена идеями с коллегами, которых я не имел возможности видеть ежедневно. Впрочем, не так уж часто бывают конференции, на которых ты решаешься изменить направление своей деятельности. Причем дважды.

Общаясь со своими коллегами на протяжении конференции, я случайно упомянул, что нашел возможный способ раз и навсегда опровергнуть Калаби. После непродолжительных уговоров я согласился посвятить один из вечеров неофициальному обсуждению своей идеи, хотя уже запланировал несколько официальных докладов. На мое выступление собрались порядка двадцати человек — и атмосфера была весьма накалена. Когда же я закончил изложение своих идей, все, казалось, согласились с моей аргументацией. Калаби также присутствовал и не высказал совершенно никаких возражений. Мне вынесли личную благодарность, объявив, что своим докладом я внес большой вклад в программу конференции, и впоследствии я весьма гордился этим.

Спустя несколько месяцев Калаби связался со мной, попросив прислать ему мое опровержение его гипотезы, поскольку он «ломал голову» над некоторыми деталями моих рассуждениях. Это побудило меня засесть за более строгое доказательство. Получив письмо Калаби, я почувствовал необходимость повторить весь ход своих рассуждений еще раз. Я работал очень усердно, на протяжении двух недель практически не оставляя времени даже на сон, чем почти довел себя до состояния нервного истощения. Всякий раз, когда мне казалось, что доказательство уже почти у меня в руках, в последнюю секунду все рассыпалось буквально у меня на глазах, причем самым обидным образом. После двухнедельного мучения я решил, что с моими рассуждениями что-то не так. Единственным выходом было сдаться и попробовать начать работу в противоположном направлении. Иными словами, я пришел к выводу о том, что гипотеза Калаби должна быть истинной. Это поставило меня в весьма любопытное положение: после изнурительных попыток доказать ошибочность утверждения Калаби мне теперь предстояло доказывать его истинность. А если гипотеза верна, то все, что из нее следует, все, что слишком хорошо, чтобы быть правдой, — действительно должно быть правдой.

Доказательство гипотезы Калаби подразумевало доказательство существования риччи-плоской метрики, а это означало решение уравнений в частных производных. Не просто любых дифференциальных уравнений в частных производных, а очень нелинейных уравнений определенного типа: комплексные уравнений Монжа-Ампера.

Уравнения Монжа-Ампера получили свое название в честь французского математика Гаспара Монжа, который начал изучать уравнения такого рода во времена Французской революции, и французского физика и математика Андре-Мари Ампера, продолжившего работу над ними несколько десятилетий спустя. Работать с этими уравнениями далеко не просто.

В качестве простейшего примера из повседневной жизни, поясняющего идеи Калаби, рассмотрим плоский пластичный лист с фиксированным периметром. Предположим теперь, что этот лист либо растягивается, либо сжимается. Вопрос в следующем: как в процессе сжатия или растяжения изменяется форма листа? Растяжение средней части листа приводит к возникновению на нем выпуклости с положительной кривизной, и соответствующее решение уравнения Монжа-Ампера будет принадлежать к эллиптическому типу. И наоборот, если внутренняя часть листа сжимается, то поверхность приобретает форму седла с отрицательной кривизной во всех своих точках, — решение будет гиперболическим. Наконец, если кривизна окажется равной нулю во всех точках, то можно ожидать решения параболического типа. Всем трем случаям будет соответствовать одно и то же уравнение Монжа-Ампера, но, как указал Калаби, «решать его необходимо совершенно разными методами».

Из трех перечисленных типов дифференциальных уравнений лучше всего мы умеем решать и анализировать уравнения эллиптического типа. Эллиптические уравнения относятся к простейшему — стационарному случаю, в котором рассматриваемые объекты неподвижны в пространстве и времени. Они описывают физические системы, не изменяющиеся с течением времени, такие как барабан, мембрана которого после остановки колебаний вернулась в состояние равновесия. Кроме того, решения эллиптических уравнений считаются наиболее простыми для понимания, поскольку соответствующие им графики являются гладкими и при их анализе проблемы с сингулярностями возникают весьма редко, хотя появление сингулярностей в решениях некоторых нелинейных эллиптических уравнений не исключено.

Гиперболические дифференциальные уравнения описывают процессы, подобные волнам или колебаниям, которые никогда не достигают равновесного состояния. Решения таких уравнений, в отличие от решений эллиптических, обычно обладают сингулярностями, и работать с ними намного сложнее. Если с линейными гиперболическими уравнениями, в которых изменение одной переменной приводит к пропорциональному изменению другой, мы уже научились управляться достаточно хорошо, то каких-либо эффективных инструментов для работы с нелинейными гиперболическими уравнениями, а именно для управления возникающими в них сингулярностями, попросту не существует.

Параболические уравнения лежат примерно где-то посередине. Они описывают стабильные физические системы, такие как колеблющаяся барабанная мембрана, которые только стремятся к равновесию, но на данный момент еще его не достигли, что привносит в физическую картину зависимость от времени. Эти уравнения менее склонны к сингулярностям, чем гиперболические, и сгладить их гораздо легче, что с точки зрения сложности решения опять-таки ставит их где-то между эллиптическими и гиперболическими.

Но существуют и еще более серьезные математические проблемы. Тогда как простейшие уравнения Монжа-Ампера содержат только две переменные, в более сложных случаях количество переменных значительно больше двух. Эти уравнения выходят за рамки гиперболических — их иногда называют ультрагиперболическими, и о их возможных решениях мы знаем еще меньше. Как заметил Калаби: «Мы понятия не имеем об этих других решениях, лежащих за пределами трех известных нам, поскольку мы совершенно не способны представить соответствующую им физическую картину». Из-за неодинаковой сложности трех типов уравнений в геометрическом анализе на сегодняшний день используются в основном либо эллиптические, либо параболические уравнения. Конечно, мы заинтересованы во всех трех типах уравнений, и существует множество интереснейших задач, связанных с гиперболическими уравнениями, например уравнения поля Эйнштейна, но обратиться к их решению нам мешает отсутствие необходимых для этого инструментов.

Уравнения, используемые в гипотезе Калаби, были нелинейными эллиптическими. Несмотря на связь этих уравнений с гиперболическими уравнениями поля Эйнштейна, гипотеза Калаби основана на несколько иных геометрических структурах. В рассматриваемом нами случае мы предполагаем, что время в нашей задаче остановилось, почти как в известной сцене из «Спящей красавицы», где на протяжении сотни лет никто и ничто не может сдвинуться с места. Благодаря этому допущению в доказательстве гипотезы Калаби можно было использовать эллиптические уравнения, устранив зависимость от времени. Это стало причиной, по которой я надеялся на то, что инструменты геометрического анализа — и в том числе те, о которых уже было сказано выше, — смогут быть с успехом использованы для решения нашей задачи.

Впрочем, даже имея в своем распоряжении все необходимые инструменты, мне предстояло проделать немалую подготовительную работу. Частично это было обусловлено тем, что никто до меня не решал комплексные уравнения Монжа-Ампера для случая более чем одного измерения. Как альпинист, постоянно стремящийся к покорению новых высот, я стремился к покорению более высоких размерностей. Чтобы подготовить себя к схватке с многомерным уравнениям Монжа-Ампера, нелинейность которых сама собой подразумевалась, мы с моим другом Ш. Ченгом принялись за исследование различных многомерных случаев, начав с задач в вещественных числах с целью впоследствии перейти к более сложным комплексным уравнениям.

Для начала мы рассмотрели знаменитую задачу, выдвинутую на рубеже XX века Германом Минковским. Задача Минковского состояла в том, чтобы установить возможность или невозможность существования некоей структуры, удовлетворяющей определенному набору критериев. Рассмотрим простой многогранник. Его структуру можно охарактеризовать, подсчитав число граней и ребер и определив их размеры. Задача Минковского состояла в обратном: можно ли, зная форму, площадь, число и ориентацию граней, определить, существует ли в действительности многогранник, удовлетворяющий данным критериям, и если да, то будет ли он единственным?

Задача на самом деле была более общей, поскольку имела отношение не только к многогранникам, но и в принципе к любым выпуклым поверхностям. Вместо того чтобы говорить об ориентации граней, с равным успехом можно говорить о кривизне, указав для каждой точки поверхности направление перпендикулярных к ней — нормальных векторов, что соответствует ориентации поверхности в пространстве. После этого уже можно задаться вопросом, существует ли объект с указанной кривизной.

Удобно, что эта задача может быть представлена не только в геометрической форме. Она также может быть записана в виде дифференциального уравнения в частных производных. По словам Эрвина Лутвака из Политехнического института при Нью-Йоркском университете: «Если вы сможете решить геометрическую задачу, то автоматически получите дополнительный приз: решение сложнейшего дифференциального уравнения в частных производных. Такая взаимосвязь между геометрией и дифференциальными уравнениями в частных производных делает эту задачу столь важной».

Мы с Ченгом нашли способ решения этой задачи, и наша статья, посвященная этому вопросу, вышла в 1976 году. Как выяснилось, другое решение было представлено несколькими годами раньше — в 1971 году российским математиком Алексеем Погореловым. Ни я, ни Ченг никогда не видели его статьи, поскольку она была опубликована на родном языке Погорелова. В конце концов, все свелось к решению сложнейшего дифференциального уравнения в частных производных из тех, которые никогда до этого не решались.

Несмотря на то что никому до нас не удавалось решить проблему данного типа, за исключением Погорелова, работа которого была нам неизвестна, процедура, позволяющая работать с нелинейными дифференциальными уравнениями в частных производных, на тот момент была уже хорошо разработана. Метод работы с подобными уравнениями, получивший название метода непрерывности, был основан на использовании последовательных приближений. И хотя этот общий подход никоим образом нельзя было назвать новым, особенность состояла в том, что каждая конкретная задача предусматривала разработку своей собственной стратегии, необходимой для ее решения. Основная идея заключалась в последовательной аппроксимации решения различными функциями так, чтобы каждое следующее приближение давало результаты лучше, чем предыдущее. Суть доказательства состояла в том, чтобы показать, что после достаточно большого числа итераций приближенная функция с большой точностью совпадет с решением искомого дифференциального уравнения. В случае удачи полученное путем аппроксимации приближение нужно рассматривать не как решение дифференциального уравнения, которое можно представить в виде определенной формулы, а как доказательство того факта, что решение существует. Для гипотезы Калаби и других задач того же типа существование решения дифференциального уравнения в частных производных эквивалентно доказательству существования определенной геометрии для заданных «топологических» условий. Это не означает, что вы ничего не знаете о решении, существование которого только что доказали. Схема, которая была использована для доказательства существования решения, зачастую может быть легко преобразована в численный метод для приближенного решения на компьютере. О численных методах речь пойдет в девятой главе.

Рис. 5.1. Математик Ш. Ю. Ченг (фотография Джорджа М. Бергмана)

Метод непрерывности был назван так потому, что он подразумевает непрерывное преобразование решения некоего известного уравнения вплоть до его полного совпадения с решением искомого. Процедуру преобразования, как правило, разбивают на две части, одна из которых работает только в непосредственной близости от известного решения.

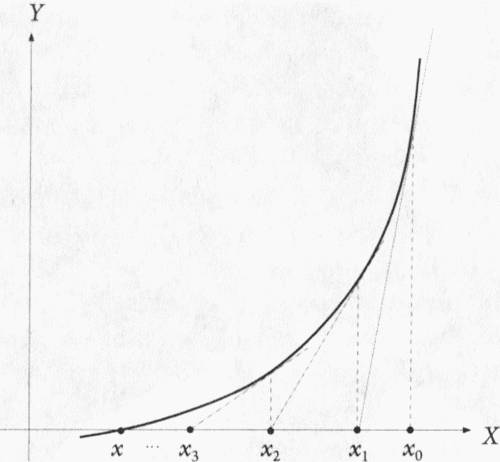
Рис. 5.2. Наглядная иллюстрация метода Ньютона. Для того чтобы найти точку пересечения определенной кривой или функции с осью X, сначала нужно наугад подобрать некую точку x₀ наиболее подходящую для этого. Затем необходимо провести касательную к кривой в точке x₀ и отметить точку, в которой эта касательная пересечет ось X (это будет точка x₁). В том случае, если наше изначальное предположение не было полностью ошибочным, продолжая этот процесс, мы будем получать точки все ближе и ближе к искомой

Одна из этих частей носит название метода Ньютона, так как она в определенной степени основана на методе, разработанном Исааком Ньютоном более трехсот лет назад. Для того чтобы продемонстрировать этот метод в действии, рассмотрим функцию y=x³-3x+1, которая описывает кривую, пересекающую ось X в трех различных точках, являющихся корнями этого полинома. Подход, предложенный Ньютоном, позволяет определить положение корней на оси X, что далеко не всегда можно сделать, просто взглянув на уравнение. Предположим, что напрямую решить уравнение нельзя, однако один из корней соответствующей функции можно найти вблизи точки x₁. Касательная, проведенная к кривой в этой точке, пересечет ось X в другой точке — x₂, находящейся ближе к искомому корню, чем точка x₁. Если мы проведем касательную в точке x₂, она пересечет ось X в точке x₃, которая будет еще ближе к искомому корню. Таким образом, многократное повторение данной процедуры должно довольно быстро привести нас к искомому корню, если только начальная точка x₁ была выбрана более-менее удачно.

В качестве еще одного примера рассмотрим набор уравнений E_t только одно из которых, Е₀ (для которого t = 0), мы способны решить. При этом в действительности нам нужно решить уравнение E₁ (для которого t = 1). Мы могли бы использовать метод Ньютона, если мы находимся в непосредственной близости к точке t = 0, решение уравнения в которой хорошо известно, но этот подход не может привести нас к 1. В этом случае необходимо прибегнуть к другому методу оценки, обладающему большей применимостью.

Как же это сделать? Представим, что над Тихим океаном была запущена ракета, которая приземлилась в радиусе ста миль от атолла Бикини. Это дает нам некоторое представление о том, где ракета может быть, другими словами — ее общую позицию, но мы хотели бы знать больше, например ее скорость, или ее ускорение, или как это ускорение изменялось в течение полета. Это можно сделать при помощи дифференциального исчисления — путем взятия первой, второй и третьей производных от функции, описывающей зависимость положения ракеты от времени. С таким же успехом можно брать производные и более высоких порядков, но для эллиптических уравнений второго порядка того типа, которым я занимаюсь, третьей производной вполне хватает.

Одного лишь знания производных функции недостаточно, хотя задача по их нахождению сама по себе может быть чрезвычайно трудоемкой. Кроме того, производные нужно «контролировать». Иными словами, необходимо установить для них границы — удостовериться, что они не могут быть ни чрезвычайно велики, ни чрезвычайно малы. Только в этом случае полученные решения будут «стабильны» — то есть не будут бесконтрольно раздуваться, тем самым дисквалифицируя себя как решения и разрушая наши надежды на них. Итак, взяв для начала нулевую производную — то есть исходную функцию, описывающую изменение положения ракеты с течением времени, мы устанавливаем для нее наличие верхних и нижних границ — иными словами, делаем оценки, показывающие, что решение по крайней мере возможно. Та же самая операция проводится для всех производных более высоких порядков, что позволяет удостовериться в том, что они не являются ни бесконечно большими, ни бесконечно малыми, а функции, их описывающие, не флуктуируют совершенно беспорядочным образом. Это позволяет априори оценить скорость, ускорение, зависимость ускорения от времени и т. д. Если мы можем таким образом проверить все производные от нулевой до третьей, значит, у нас есть хороший способ оценить уравнение в целом и приличный шанс найти его решение. Подобный процесс оценки и доказательства того, что оценочные данные сами по себе находятся под контролем, как правило, представляют самую сложную часть всего процесса.

Итак, в конце концов, все сводится к оценкам. Есть что-то ироническое в моем признании их актуальности для решения проблемы, с которой я столкнулся. Помню, когда я впервые попал в Беркли, в коридоре математического факультета я столкнулся с двумя постдоками из Италии. Они прыгали с радостными криками. На мой вопрос о том, что произошло, они ответили, что им только что удалось получить приближенную оценку. Когда же я спросил их о том, что это такое — оценка, они посмотрели на меня как на полного невежду, непонятно как попавшего в это здание. Именно с этого момента я пытался узнать как можно больше об априорных оценках. Калаби получил такой же урок несколькими десятилетиями ранее от своего друга и соратника Луиса Ниренберга: «Повторяй за мной, — говорил тогда Ниренберг, — без априорных оценок ты никогда не сможешь решать дифференциальные уравнения в частных производных!» А в начале 1950-х Калаби переписывался с Эндрю Вейлем по поводу своей гипотезы. Вейль, который полагал, что математические технологии того времени просто не созрели для нахождения решения, спрашивал Калаби: «Как вы собираетесь получить оценки?»

Два десятилетия спустя, когда я включился в игру, сама проблема не изменилась. Она по-прежнему оставалась невероятно сложной, хотя математический аппарат за это время успел развиться настолько, что решение стало в принципе возможным. Проблема состояла лишь в том, чтобы найти верный подход или, по крайней мере, создать необходимую точку опоры. Так что я подобрал более простое уравнение, а затем постарался показать, что его решение может в конечном счете «деформироваться» в решение более сложного уравнения.

Предположим, что вам нужно решить уравнение f(x) = x²-x при f(x) = 0. Подставим для начала x = 2 и убедимся, что этот вариант не подходит: f(2) = 2, а не 0. Тем не менее у нас теперь есть решение, если не для исходного уравнения, то для чего-то подобного. Перепишем первоначальное уравнение как f(x) = 2t. Для случая t = 1 его решение уже известно (x = 2), и теперь задача состоит в том, чтобы решить его при t = 0. Как же это сделать? Рассмотрим параметр t. Что произойдет, если немного изменить значение t, так, чтобы оно уже не было равно точно 1, но все же оставалось близким к единице? Интуиция подсказывает, что если t будет близко к 1, значение f(t) будет близко к 2. Это предположение оказывается верным для большинства случаев, а это означает, что при t близком к 1 мы можем решить уравнение.

Теперь будем уменьшать t, так чтобы рано или поздно его значение достигло нуля и в результате мы получили исходное уравнение. Выбирая все меньшие и меньшие значения t, будем записывать для каждого из них соответствующие решения уравнения. В результате возникнет последовательность точек, в которых решение уравнения существует, и каждой из этих точек соответствует собственное значение x, которое я буду называть x_i. Смысл этого упражнения заключается в том, чтобы доказать, что последовательность x_i сходится к определенному значению. Для этого нужно показать, что x_i ограниченно и не может возрастать до бесконечности, потому что для любой ограниченной последовательности по крайней мере некоторые ее части должны сходиться. Показав сходимость x_i, мы тем самым покажем возможность уменьшения величины t до 0 без столкновения с какими-либо непреодолимыми препятствиями. И если мы сможем это сделать, мы тем самым решим уравнение, показав, что случай с t = 0 также имеет решение. Иными словами, мы покажем, что решение исходного уравнения x²-х=0 должно существовать.

Именно такие рассуждения я использовал при доказательстве гипотезы Калаби. Ключевым моментом доказательства стала необходимость показать, что x_i представляют собой сходящуюся последовательность. Конечно, уравнение, лежащее в основе гипотезы Калаби, было намного сложнее, чем x²-х=0. В этом уравнении в роли x выступало не число, а функция, что безмерно увеличивало сложность, поскольку сходимость последовательности функций доказать, как правило, весьма и весьма непросто.

Итак, мы снова разбиваем большую проблему на более мелкие фрагменты. Уравнение, входящее в гипотезу Калаби, является эллиптическим уравнением второго порядка, и для решения подобных уравнений необходимо сделать оценки нулевого, первого, второго и третьего порядков. Сделав эти оценки и доказав, что они сходятся к желаемому решению, можно считать гипотезу доказанной. Это легче сказать, чем сделать, поскольку нахождение этих четырех оценок представляет собой отнюдь не простую задачу. Думаю, именно за способность делать такие вещи нас и ценят.

Впрочем этим наша с Ченгом подготовка к наступлению на уравнения Монжа-Ампера не ограничилась. Мы начали работу над так называемой проблемой Дирихле, названной в честь немецкого математика Лежёна Дирихле. Эта проблема относилась к категории краевых задач, решение которых, как правило, представляет собой первый этап решения эллиптических дифференциальных уравнений. Примером краевой задачи может служить проблема Плато, затронутая в третьей главе, которую обычно поясняют на примере мыльных пленок и которая утверждает, что для произвольного замкнутого контура всегда можно найти минимальную поверхность, ограниченную этим контуром. Каждая точка такой поверхности в действительности является решением определенного дифференциального уравнения. Иными словами, вопрос сводится к следующему: если известно граничное решение такого уравнения, то можно ли найти поверхность в целом и таким образом полностью решить уравнение? Несмотря на то что гипотеза Калаби не является краевой задачей, мы с Ченгом нуждались в проверке методов, которые могли впоследствии пригодиться нам в работе над комплексными уравнениями Монжа-Ампера типа того, что фигурирует в гипотезе Калаби. Для этого мы занялись решением задачи Дирихле в определенных областях комплексных евклидовых пространств.

Решить задачу Дирихле можно при помощи уже упомянутых ранее шагов, оценивая значения производных нулевого, первого, второго и третьего порядка для точек, лежащих на границе. Но мы должны сделать такие же оценки и для внутренних точек поверхности, поскольку рассматриваемый «мыльный пузырь» может иметь разрывы, сингулярности и другие отклонения от гладкости. Таким образом, общее число оценок равно восьми.

Рис. 5.3. Математик Луис Ниренберг

К началу 1974 года Калаби и Ниренберг, также работавшие над задачей Дирихле, одновременно с нами получили оценку второго порядка. Нахождение оценки нулевого порядка оказалось весьма простой задачей. Ну а оценку первого порядка можно вывести из оценок нулевого и второго порядков. Итак, оставалась только оценка третьего порядка, нахождение которой и открывало путь к решению задачи Дирихле.

Математический аппарат, необходимый для решения этой задачи, возник еще в конце 1950-х. Я еще учился в средней школе, когда Калаби нашел решение главной геометрической задачи, оказавшейся впоследствии решающей в вопросе нахождения оценок третьего порядка для внутренних точек поверхности в случае вещественных уравнений Монжа-Ампера. Сделать вклад в эту область Калаби во многом помогло стечение обстоятельств. В то время он работал над проблемой из области аффинной геометрии (аффинная геометрия представляет собой обобщение евклидовой геометрии, в подробности которого я, будучи весьма далек от этой области, не особо хочу вдаваться), тогда как Ниренберг и Чарльз Левнер из Стэнфордского университета занимались задачей Дирихле для уравнения Монжа-Ампера, но не с гладкой, а с так называемой сингулярной границей, подобной гребню волны. Увидев то уравнение, над которым работали Ниренберг и Левнер, Калаби понял, что оно непосредственно связано с тематикой его работ по аффинной геометрии. Калаби и Ниренберг догадались, как применить результаты Калаби, полученные им в 1950-х годах, к проблеме оценки третьего порядка для внутренних точек поверхности, с которой мы столкнулись в 1970-х. «Многие математические открытия происходят благодаря удачному стечению обстоятельств, такому как это, — заметил Калаби. — Порой стоит попробовать соединить кажущиеся несовместимыми идеи и затем посмотреть, где можно применить то, что получилось в результате».

Позже, в 1974 году, Калаби и Ниренберг объявили, что им удалось найти решение краевой задачи для комплексных уравнений Монжа-Ампера. Впрочем, оказалось, что они допустили ошибку, и оценка третьего порядка для точек, находящихся на границе, по-прежнему отсутствовала.

Вскоре мы с Ченгом представили и свою версию оценки третьего порядка на границе. Это произошло во время обеда, на который Ч. Ш. Черн пригласил нас, чтобы мы составили компанию ему с Ниренбергом. Ниренберг в то время уже был большой шишкой, тогда как мы только окончили университет, поэтому всю ночь перед предполагавшимся обедом мы посвятили проверке нашего доказательства и, к нашему ужасу, обнаружили в нем ошибки. На их исправление и переписывание доказательства нам потребовалась целая ночь. Следующим вечером мы показали наше доказательство Ниренбергу. Он остался им доволен, мы также остались им довольны, так что теперь можно было спокойно наслаждаться обедом. Но уже после обеда мы с Ченгом заново просмотрели доказательство и нашли в нем новые ошибки. Только через шесть месяцев после этого, в самом конце 1974 года, мы закончили работу над краевой задачей. Нам удалось решить ее путем исследования уравнения, близкого к тому, над которым работали Левнер и Ниренберг, только для более высоких размерностей. Метод, который мы использовали, позволял не принимать во внимание оценку третьего порядка, делая ее необязательной.

Закончив эту работу, я был готов приступить к комплексному варианту гипотезы Калаби — задаче, которая, в отличие от задачи Дирихле, сформулированной для комплексного евклидова пространства, относилась к случаю комплексного многообразия. Мое стремление как можно быстрее приступить к ее доказательству было столь сильным, что к публикации статьи, посвященной задаче Дирихле, мы смогли вернуться только через пять лет — в 1979 году.

Когда задача Дирихле осталась позади, большая часть оставшейся работы представляла собой обобщение или, иными словами, перевод оценок, сделанных для вещественных уравнений Монжа-Ампера, в оценки для комплексных уравнений. Этот путь мне пришлось преодолевать уже в одиночку, поскольку дороги Ченга лежали немного в другом направлении.

Когда-то, в 1974 году, Калаби и Ниренберг совместно с Дж. Дж. Коном из Принстона уже начинали работу над комплексной разновидностью задачи Дирихле в евклидовом пространстве. Они добились определенных успехов в исследовании оценок третьего порядка, так что мне оставалось применить их результаты к случаю искривленного пространства. В том же году у меня возникли некоторые идеи по поводу нахождения оценок второго порядка для гипотезы Калаби, при этом я опирался на собственную работу 1972 года, посвященную так называемой лемме Шварца. Эта лемма, или мини-теорема, появилась еще в XIX столетии и не имела ничего общего с геометрией, до тех пор пока в первой половине XX столетия она не была переосмыслена профессором Гарвардского университета Ларсом Альфорсом. Теорема Альфорса относилась только к римановым поверхностям, имеющим по определению одно комплексное измерение, но мне удалось обобщить ее для случая любой комплексной размерности.

Приготовления к поиску оценки второго порядка для гипотезы Калаби я закончил летом 1975 года. Год спустя я узнал, что французский математик Тьерри Обен нашел подход к данной оценке независимо от меня. Сделав оценку второго порядка, я также показал ее зависимость от оценки нулевого порядка и продемонстрировал возможность перехода от нулевого порядка ко второму. После окончания работы над этой оценкой оставался только один нерешенный вопрос, от которого теперь зависела судьба всего доказательства, — нахождение оценки нулевого порядка. Из оценки нулевого порядка я уже мог получить оценку как второго, так и первого порядка — в качестве бесплатного приложения к уже найденным, поскольку из оценок нулевого и второго порядков оценка первого порядка следует автоматически. Это было чистой воды везение. Фигурально выражаясь, так легли карты и, в целом, легли они весьма неплохо. Оценка третьего порядка также оказалась зависящей от оценок нулевого и второго порядков — то есть все свелось к нахождению оценки нулевого порядка. Знание этой оценки должно было расставить все остальное на свои места, но без нее все прочее было бы бессмысленно.

Свою работу я заканчивал в Курантовском институте Нью-Йорка, находясь на должности приглашенного сотрудника — эту должность мне помог занять Ниренберг. Вскоре моя невеста Ю-Юн, работавшая до этого в Принстоне, получила предложение работы в Лос-Анджелесе. Не желая разлучаться с ней, я занял другую приглашенную должность в Калифорнийском университете. В 1976 году мы вместе проехали всю страну с востока на запад, собираясь заключить брак сразу же по прибытии в Калифорнию. И действительно, прибыв в Калифорнию, мы тут же обвенчались. Эта поездка запомнилась нам надолго: мы были влюблены друг в друга, природа вокруг поражала своей красотой и большую часть пути мы строили планы на будущую совместную жизнь. Но все же я должен признаться, что даже тогда было нечто, что не давало мне покоя: в моей голове по-прежнему крепко сидела гипотеза Калаби и, в частности, оценка нулевого порядка, которая никак мне не поддавалась. Целый год я бился над ее поисками. В сентябре 1976 года, сразу после нашей свадьбы, мои усилия, наконец, увенчались успехом, и остальные части доказательства тут же встали на свои места. Как оказалось, семейная жизнь была именно тем, чего мне недоставало.

Задача нахождения оценки нулевого порядка аналогична нахождению оценок других порядков: на некое уравнение или функцию необходимо наложить ограничения — как сверху, так и снизу. Иными словами, функцию нужно поместить в воображаемый ящик и показать, что функция «влезет» в него, даже если размеры ящика не будут бесконечно велики. Если это возможно сделать, то функцию можно считать ограниченной сверху. С другой стороны, нужно показать, что функция не настолько мала, чтобы каким-либо образом «просочиться» за пределы ящика, таким образом ограничив ее снизу.

Один из возможных подходов к задаче такого типа состоит в том, чтобы взять абсолютное значение — модуль функции, которое говорит о ее величине в целом вне зависимости от того, положительное или отрицательное значение она принимает. Для того чтобы проверить функцию u, нужно показать, что ее абсолютное значение в любой точке пространства будет меньше постоянной величины c (или равно ей). Поскольку значение c точно определено, необходимо просто показать, что функция u не может произвольно принимать очень большие или очень малые значения. Иными словами, утверждение, которое мы хотим доказать, является простым неравенством, утверждающим, что модуль функции u должен быть меньше или равен c: |u|≤c. И хотя оно выглядит не особо сложным, в том случае, когда u является комплексным объектом, доказательство требует достаточно много усилий.

Я не буду подробно останавливаться на деталях доказательства, отмечу только, что оно основывалось на оценке второго порядка для уравнения Монжа-Ампера, которую я уже сделал ранее. Мне также пригодилось известное неравенство Пуанкаре, а также неравенство, полученное российским математиком Сергеем Соболевым. Оба они содержали возведенные в определенную степень интегралы и производные различных порядков от абсолютного значения u. Последнее, а именно нахождение различных степеней интегралов и производных от u, имело решающее значение для проведения оценок, поскольку, только показав, что интегралы и производные от u в степени p даже при очень больших p все равно остаются ограниченными, можно считать работу выполненной. После этого функцию можно было считать стабильной. В конце концов, с помощью этих неравенств и различных теорем, а также ряда лемм, сформулированных мной по ходу доказательства, я смог это сделать. Когда, наконец, оценка нулевого порядка была получена, работу можно было считать завершенной.

Впрочем, говорят, что нельзя судить о пудинге до тех пор, пока его не попробуешь, — даже если что-то имеет привлекательный вид, окончательный вывод можно сделать только после тщательной проверки. Я не мог слепо полагаться на удачу. Однажды я уже поставил себя в неловкое положение, публично заявив на стэнфордской конференции 1973 года, будто знаю, как опровергнуть гипотезу Калаби. Тогда мое предполагаемое опровержение провалилось, и если бы теперь точно так же провалилось и мое подтверждение гипотезы Калаби, моя репутация как математика оказалась бы под большим вопросом. Я точно знал, что на данном этапе своей карьеры — мне тогда еще не исполнилось тридцати — я не могу позволить себе ошибиться вновь, по крайней мере, в столь важном деле.

Поэтому я проверял и перепроверял свое доказательство, рассмотрев его четыре раза с четырех совершенно разных позиций. Я проверял его столько раз, что поклялся, что если я окажусь неправ, то брошу математику. Но все мои попытки найти огрехи в доказательстве оказались тщетными. Насколько я мог судить, в нем все было идеально. Поскольку в те времена еще не существовало Интернета, где я мог бы просто опубликовать черновик своей статьи и попросить прокомментировать его, я избрал старомодный путь — выслал копию моего доказательства Калаби и отправился в Филадельфию для дальнейшей дискуссии с ним самим и другими геометрами с математического факультета Пенсильванского университета, в том числе и с Джерри Кадзаном.

Калаби счел мое доказательство безупречным, но мы договорились встретиться с Ниренбергом и проработать его вместе шаг за шагом. Так как найти время, когда мы все трое были бы свободны, было весьма непросто, наша встреча пришлась на Рождество 1976 года — единственный день, в который никто из нас не имел неотложных дел. На этой встрече нам так и не удалось найти в доказательстве ни одной ошибки — впрочем, чтобы окончательно удостовериться в правильности доказательства, требовалось намного больше времени. «На первый взгляд оно выглядит весьма правдоподобно, — вспоминал Калаби. — Но чрезвычайная сложность этого доказательства требует еще порядка месяца для более детальной проверки».

По окончании срока, отпущенного на рецензирование, Калаби и Ниренберг выразили свое полное согласие с моим доказательством. С этого момента гипотезу Калаби можно было объявить доказанной, и за прошедшие с того времени тридцать с лишним лет никто так и не смог поколебать это утверждение. На сегодняшний день доказательство гипотезы Калаби выдержало столько проверок, проведенных столь значительным числом ученых, что едва ли можно ожидать обнаружения в нем существенных ошибок в дальнейшем.

Итак, что же мне удалось сделать? Доказательством гипотезы Калаби я еще раз укрепил свое убеждение о том, что важнейшие математические проблемы могут быть разрешены путем объединения геометрии с дифференциальными уравнениями в частных производных. Более конкретно, я доказал существование риччи-плоской метрики для компактных кэлеровых пространств, первый класс Черна для которых обращается в нуль, хотя я и не смог написать точную формулу, определяющую метрику саму по себе. Все, что я мог сказать, — это то, что подобная метрика существовала, но точный ее вид так и остался мне неизвестным.

Хотя это может прозвучать несколько неожиданно, метрика, существование которой я доказал, обладала почти сверхъестественными свойствами. В качестве постскриптума к своему доказательству я показал возможность существования множества фантастических многомерных пространств, известных сейчас как пространства Калаби-Яу, которые удовлетворяли уравнениям Эйнштейна в случае отсутствия в них материи. Таким образом, я обнаружил не просто решение, а самый многочисленный из известных класс решений уравнений Эйнштейна.

Кроме того, мне удалось показать, что непрерывно изменяя топологию, можно получить бесконечный класс решений основного уравнения, входящего в гипотезу Калаби, в настоящее время известного как уравнение Калаби-Яу и являющегося частным случаем уравнения Эйнштейна. Решения этого уравнения представляли собой топологические пространства, и сила доказательства состояла в его общности. Иными словами, я доказал существование не только одного примера подобных пространств или частного случая, а целого класса примеров. Более того, я показал, что для определенной топологии — например, для комплексных подмногообразий, находящихся внутри более крупных многообразий, — существует только одно возможное решение.

До появления моего доказательства единственными известными компактными пространствами, удовлетворяющими требованиям уравнений Эйнштейна, были так называемые локально однородные многообразия, в которых любые находящиеся рядом две точки казались неразличимыми. Но те пространства, которые мне удалось обнаружить, были как неоднородны, так и асимметричны, точнее, в них отсутствовала всеохватывающая глобальная симметрия, что, однако, не мешало им иметь менее заметную внутреннюю симметрию, о которой уже шла речь в предыдущей главе. Лично для меня это казалось преодолением огромного препятствия, поскольку выход за пределы глобальной симметрии открывал целый ряд новых возможностей, делая мир вокруг и интереснее и запутаннее.

В первое время я просто наслаждался красотой этих замысловатых пространств и кривизны самой по себе, не задумываясь об их возможных применениях. Но уже вскоре оказалось, что эти пространства имеют множество применений, как в рамках математики, так и за ее пределами. Однажды мы уже сочли гипотезу Калаби «слишком хорошей, чтобы быть истинной». На самом деле она оказалась даже лучше, чем мы думали.