Эта теория является одним из вариантов векторнотензорных теорий гравитации и, пожалуй, самая популярная на настоящий момент. Именно поэтому мы рассказываем о ней. Теория была предложена в 2009 году американским теоретиком- “струнником» чешского происхождения Петром Хоржавой. Она несколько отличается от обычных векторно–тензорных теорий, поскольку в ней вместо векторного поля используется градиент скалярного. С одной стороны, сохраняются свойства векторных теорий, с другой — есть специфические собственные полезные свойства.

Ещё раз вспомним, что непротиворечивую квантовую теорию гравитации, в которой не было бы расходимостей, на основе ОТО создать не удалось. Поэтому предлагаются различные модификации, которые на квантовых масштабах существенно расходятся с ОТО и становятся «подходящими» для квантования. Для этого при их построении некоторые принципы, лежащие в основе ОТО, изменяются, т. е. оказываются нарушенными. Конечно, это нарушение должно быть настолько незначительным, чтобы не противоречить лабораторным тестам, и чтобы не изменилось действие теории на масштабах планетных систем, где есть хорошее соответствие с наблюдениями. Именно такой является теория Хоржавы, Мы не будем рассказывать насколько она замечательна в смысле квантования, это несколько в стороне от темы книги, зато расскажем о её свойствах как гравитационной теории — в чем и насколько они отличны от аналогичных свойств ОТО.

Лоренц–ннвариантность. Мы уже обсуждали тот факт, что ОТО как бы «выросла» из специальной теории относительности — механики высоких скоростей, сравнимых со скоростью света. Напомним, что в СТО все инерциальные системы отсчёта, движущиеся относительно друг друга равномерно и прямолинейно, эквивалентны. Важно вспомнить об измерениях времени в СТО. В каждой инерциальной системе отсчёта часы идут в своём собственном темпе, отличном от темпа часов других систем, если их сравнивать. Однако нельзя выбрать ни «лучший», ни «худший» темп, если часы конструктивно идентичны. То есть собственное время каждой инерциальной системы равноправно в отношении других. Это означает, что в СТО нет выделенного течения времени.

Мы также говорили, что на геометрическом языке инвариантность в СТО при переходе от одной инерциальной системы отсчёта к другой эквивалентна инвариантности относительно лоренцевых вращений во всем плоском пространстве–времени. В ОТО из-за «включения» гравитации и, соответственно, искривления пространства-времени лоренц–инвариантность во всем пространстве–времени уже невозможна. Тем не менее, ОТО остаётся лоренц–инвариантной локально, то есть в малой окрестности каждого наблюдателя. Эта инвариантность является одним из принципов, лежащих в основе ОТО, и связана с принципом соответствия ОТО и СТО.

Хронометрическая теория. В ряде модификаций ОТО нарушена как раз локальная лоренц–инвариантность. Среди них и теория Хоржавы. В последнее время особой популярностью пользуется одна из её реализаций, так называемая «жизнеспособная» («healthy») не проективная версия, разрабатываемая американскими физиками Диего Власом и Ориолом Пуйоласом и нашим соотечественником Сергеем Сибиряковым. Эффекты, обсуждаемые ниже, в основном относятся именно к этой модификации ОТО.

Итак, чем же теория Хоржавы отличается от ОТО? В дополнение ко всем обычным полям ОТО добавляют скалярное поле φ, но не обычным образом. Направление его изменения в пространстве–времени определяет специально выделенное направление времени. Именно поэтому скалярное поле называют полем хронона. Тогда поверхности постоянных значений скалярного поля — это поверхности постоянного времени, или «одновременности». В уравнения скалярное поле входит только через производные, поэтому не стоит опасаться бесконечных значений поля хронона. Существенным является только его изменение, а не значения. Поскольку в пространстве- времени есть выделенное направление, то существуют выделенные системы отсчёта. Это не свойственно ни СТО, ни ОТО, но свойственно векторно–тензорным теориям. Для наглядности приведём простейший «игрушечный» пример. Одно из решений новой теории — это плоское пространство–время (такое как в СТО) плюс поле хронона, которое оказывается просто временем, φ = t. В СТО мы можем перейти с помощью лоренцевых преобразований из одной координатной системы х, t в другую х', t', где время течёт по–другому, В новой теории — не можем, поскольку значение скалярного поля при координатных преобразованиях не меняются, а это есть время. Таким образом, здесь, в отличие от СТО, существуют часы, которые отсчитывают выделенное время.

Поскольку в ОТО гравитационным полем является поле метрики пространства–времени, то ясно, почему новую теорию называют хронометрической. Допустимые ограничения на параметры хронометрической теории дают возможность избежать расходимости при квантовании. Ещё раз повторим: это и было главной целью её построения. Но это теоретический успех, а проверить квантовые эффекты такого уровня сейчас вряд ли возможно.

Однако новая теория должна измениться и в классических (не квантовых) проявлениях. А это даёт возможность доказать или опровергнуть её право на существование. Далее мы покажем, в каких классических явлениях и насколько хронометрическая теория отличается от ОТО, можно ли выявить в наблюдениях эффекты новой теории, проиллюстрируем разницу для некоторых теоретических моделей. Для этого обсудим наиболее яркие, на наш взгляд, примеры.

Гравитационно–волновое излучение. Вспомним, что гравитационная волна в ОТО — поперечная, тензорная, имеет две поляризации (см. рис. 10.2) и распространяется со скоростью света. Гравитационные волны в теории Хоржавы также существуют. Однако помимо двух уже упомянутых тензорных поляризаций имеет место скалярная степень свободы. Это означает, что под действием такой волны к движению пробных частиц добавятся продольные (в направлении распространения волны) смещения. Важно то, что тензорная и скалярная составляющие имеют разные скорости распространения, Кроме того, обе скорости, имея зависимость от параметров модели Хоржавы, должны превышать (!) скорость света, хотя и незначительно. Эти отличия от ОТО интересны, но к сожалению пока только теоретически. До сих пор нет хотя бы непосредственного детектирования гравитационных волн, поэтому фиксация отмеченных различий представляется делом отдалённого будущего.

Тем не менее существует косвенное подтверждение существования гравитационного излучения. Это наблюдения за двойными пульсарами, уменьшение размеров орбит которых свидетельствует о потере энергии на гравитационно–волновое излучение. Этот эффект находится в соответствии с ОТО с относительной точностью 10–2, о чем мы уже говорили. Но предсказания ОТО и теории Хоржавы различны. Поэтому если последняя жизнеспособна, то есть шанс, что уже дальнейшее увеличение точности выявит эти различия и уточнит параметры новой теории.

Теперь для хронометрической теории рассмотрим взаимодействие гравитационного поля с веществом. Обсудим только первое (линейное) приближение, которое может быть доступно для наблюдений. В этом порядке эффекты, связанные с нарушением лоренц–инвариантности, подавлены в силу различных причин, но поле хронона присутствует, оно включено лоренц–инвариантным образом в так называемую эффективную метрику. То есть метрика ОТО модифицируется, и материя распространяется не в исходном пространстве–времени, а в некотором эффективном пространстве–времени, причём универсальным образом. Возможно в будущем именно это взаимодействие позволит обнаружить классические явления, представленные хронометрической теорией.

В приближении слабых полей и малых скоростей пределом гравитационной теории должна стать гравитация Ньютона. В последней взаимодействие двух частиц представлено известным законом Ньютона, где сила пропорциональна массам, гравитационной постоянной, обратно пропорциональна квадрату расстояния, но не зависит от скоростей этих частиц. Присутствие поля хронона изменяет и дополняет и этот закон следующим образом. Незначительно меняется гравитационная постоянная, теперь её называют эффективной, и появляется зависимость от скоростей. Возможность детектирования этих эффектов определяется константами связи хронометрической теории.

Влияние поля хронона проявляется также в том, что некоторые взаимодействия могут распространяться мгновенно (!), т. е. с бесконечной скоростью. Как сделан этот вывод? Обычно уравнения для возмущений содержат волновой оператор, который состоит из двух частей: пространственной и временной. Величина, обратная коэффициенту при второй части — это квадрат скорости распространения возмущений. Полное отсутствие второй части означает, что эта скорость бесконечна. Именно такую структуру имеет часть уравнений теории Хоржавы. Здесь уместно провести аналогию с теорией Ньютона. В ней точно так же, как и в хронометрической теории, выделено течение времени («абсолютное время») и гравитационное взаимодействие распространяется мгновенно.

Как представить мгновенное распространение? Вообразите поверхность постоянного времени, тогда сигнал, распространяясь на ней (то есть без изменения времени), мгновенно проходит любые расстояния. Это недопустимо в таких релятивистских теориях как СТО или ОТО. Обратимся к диаграмме на рис. 12.1. Рассмотрим три точки в пространстве: А, В и С. В момент t = 0 эти точки соответствуют событиям А₀, В₀, С₀, которые, в рамках СТО причинно не связаны. Только в момент t₁ событие А₀ становится причинно связанным с событием В₁ в точке В, а в момент t₂ и с событием С₂ в точке С. Как и должно быть

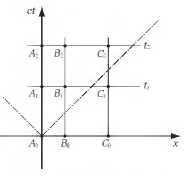
Рис. 12.1. Причинно связанные события в СТО и теории Хоржавы

в СТО (или ОТО), распространение сигналов жёстко связано и ограничено световыми конусами. В теории Хоржавы для некоторых взаимодействий это вполне может быть не так. Мгновенное распространение означает, что все три события А₀, В₀, С₀ в момент времени t = 0, произошли как следствие одного мгновенно распространяющегося сигнала, то есть они могут быть причинно связанными. Однако такая «фантастическая» возможность не ограничивает хронометрическую теорию решающим образом. Выделенность направления времени означает, что понятие одновременности определено однозначно, поэтому не возникает проблем с причинностью, хотя бы и такой экзотической.

Солнечная система. Для проверки какой-либо гравитационной теории при измерении движений в планетной системе используется ΡΡΝ–формализм. Как в любой векторной теории, в теории Хо ржавы должны присутствовать эффекты привилегированной системы отсчёта. Это приводит к тому, что оказываются ненулевыми PPN- параметры группы а. Действительно, кроме двух PPN- параметров, присущих ОТО, хронометрическая теория имеет ещё два: α₁ и α₂. Чтобы не было противоречий с наблюдениями, они должны быть достаточно малыми: α₁ ≤ 10–4 и α₂ ≤ 10–7. Будем ждать повышения точности измерений, тогда, возможно, существование α₁ и α₂ (а значит и теории Хоржавы) будет подтверждено или опровергнуто.

Чёрные дыры. В ОТО чёрная дыра представляет объект, где центральная часть, обычно сингулярная, окружена сферической поверхностью, названной горизонтом событий. Его наличие связано с тем, что в ОТО существует предельная скорость — это скорость света. Основное свойство чёрной дыры состоит в том, что в ОТО никакая частица, никакое поле и даже световой сигнал не могут её покинуть, то есть уйти за пределы горизонта событий.

В хронометрической теории есть также решения, описывающие объекты типа чёрных дыр. Однако вспомним, что в этой теории нет предельной скорости, возможно распространение взаимодействий со скоростью большей, чем скорость света и даже мгновенно. Если бы эта возможность была в ОТО, то само понятие горизонта событий потеряло бы смысл, поскольку появляется возможность покинуть объект, находясь и на горизонте событий, и под ним. При этом появляются противоречия, связанные с термодинамикой системы, такие как уменьшение энтропии. Сейчас не известны все решения для чёрных дыр в теории Хоржавы в силу её молодости, однако среди известных есть такие, которые позволяют избежать этих осложнений. Оказывается, что в чёрной дыре в рамках хронометрической теории может быть так называемый универсальный горизонт. Он находится под горизонтом событий («ближе» к сингулярности) и замечателен тем, что поверхности постоянного времени, находящиеся под ним, не пересекают его. Это означает, что сигнал даже бесконечной скорости (мгновенный) не может выйти из- под этого промежуточного горизонта. А для таких объектов вышеупомянутые противоречия снимаются.

На рис. 12.2 представлена так называемая диаграмма Пенроуза чёрной дыры Шварцшильда. Точки i_- и i₊ представляют всю временную бесконечность прошлого и всю временную бесконечность будущего, точка i₀ объединяет всю пространственную бесконечность. Прямая В i₊ является горизонтом событий шварцшильдовой чёрной дыры — это

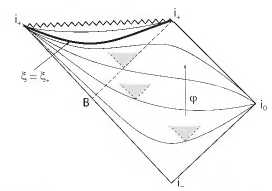
Рис. 12.2. Диаграмма хронометрической чёрной дыры

видно из расположения световых конусов. Действительно, квадрат В i₊ i₀ i_- — это все внешнее пространство–время вне горизонта событий, в то время как треугольник i₊Bi₊ — это пространство–время под горизонтом событий, откуда сигнал не может выйти во внешнюю область, и где ломаная линия — это сингулярность r = 0. На диаграмму шварцшильдовой дыры наложена диаграмма чёрной дыры хронометрической теории. Все кривые, соединяющие i₀ и i₊, — это сечения постоянного поля хронона φ = const, то же самое, постоянного времени (одновременности). Жирная дуга — это тот самый универсальный горизонт ξ=ξ_*, под ним, ближе к сингулярности, дуги i₊i₊, соединяющие концы ломаной линии — это тоже сечения постоянного времени (одновременности). Ясно, что если сигнал в хронометрической теории распространяется даже мгновенно, то есть вдоль сечений одновременности, то он не сможет пересечь универсальный горизонт и покинуть хронометрическую чёрную дыру.

Космология. В масштабах Вселенной теория Хоржавы также имеет шанс заявить о своей жизнеспособности. Обсудим космологические решения в новой теории. Они будут примерно такими же, как в ОТО, с той разницей, что вместо обычной гравитационной постоянной G будет фигурировать эффективная гравитационная постоянная G_E. Теперь вспомним модифицированный закон Ньютона, о котором говорилось выше. Там появляется своя эффективная гравитационная постоянная, отличная от G, обозначим её G_I. Сделаны оценки для разницы: |G_I-GE| ≤ 0,1. Нет запрета на то, что в будущем будет определена значимая величина для этой разницы, но так же возможно, что она будет исключена.

На основе ОТО разработана хорошо согласованная с наблюдениями теория космологических возмущений. Она позволяет, например, объяснить структуру, то есть распределение галактик и их скоплений в доступной наблюдениям области Вселенной. Тем не менее, если при повышении точности наблюдений будет обнаружена, скажем, анизотропия, не предсказанная ОТО, то это повод обратиться к теории Хоржавы. Теория Хоржавы настолько молода, что вряд ли её саму и выводы, сделанные на её основе, можно считать устоявшимися и всеми признанными. Несмотря на это, как теория в целом, так и выводы, представляются очень интригующими и важными.