Вернёмся к парадоксам не релятивистской космологии. Вспомним, что причина гравитационного парадокса в том, что для однозначного определения гравитационного воздействия либо недостаточно уравнений, либо нет возможности корректно задать граничные условия. В случае фридмановской космологии независимыми являются два уравнения Эйнштейна. Учитывается также уравнение состояния (связи между плотностью и давлением). Кроме того, на данный момент времени из наблюдений известны плотность и скорость расширения,

Все это однозначно определяет эволюцию масштабного фактора a(t), плотность ρ и давление р. Становится известной геометрия космологического пространства–времени, а значит, тип и динамика 3–мерного пространства, в котором звезды, галактики, скопления галактик ведут себя в соответствии с современными наблюдениями. То есть гравитационного парадокса не возникает.

Теперь зададимся, возможно, провокационным вопросом. А можно ли описать расширяющуюся Вселенную с помощью гравитации Ньютона? Оказывается, можно! Обратимся к опыту Зельдовича. В своих лекциях он всегда старался представить материал простейшим способом, а рассказывая о космологических решениях, по возможности ограничивался теорией Ньютона.

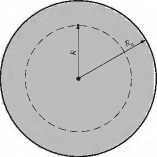
Рис 9.4. Схема расчёта ускорений

Рассмотрим шар радиуса R₀ и элемент массы m внутри шара на расстоянии от центра R < R₀ (рис. 9.4).

Такая задача рассматривалась ещё Ньютоном. Он же и установил, что сила, действующая на m, определяется массой материи внутри сферы радиуса R, а гравитационное действие внешних областей взаимно компенсируется:

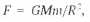
здесь: Μ = (4π/3)R³ρ — масса материи внутри сферы, ρ — плотность материи, распределённая однородно. Следовательно, ускорение

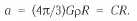
Таким образом, ускорение элемента в точке R пропорционально его расстоянию от центра и не зависит от радиуса шара R₀ при любом, сколь угодно большом R₀. Это фактически означает, что соотношение справедливо для бесконечной однородной вселенной.

Но остаётся вопрос: решение было найдено для некоторого центра, в котором ускорение равно нулю, а в других точках имеет вполне определённую величину и направлено к центру. А где такой центр в бесконечной однородной вселенной? На самом деле, никакого выделенного центра нет или, если угодно, таким центром может быть любая точка, Возьмём произвольную точку O' находящуюся на некотором расстоянии R_O' от «нашего» центра, ускорение которой a_O'=-CR_O'. Радиус–вектор и ускорение направлены, разумеется, в разные стороны.

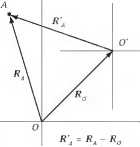
Рис. 9.5. Переход к другой системе координат

Перейдём в систему координат с центром в точке O'

(рис. 9.5). Величины в этой новой системе координат будем обозначать штрихом.

Ускорения в старой и новой системах координат связаны правилом Галилея, которое, если кто забыл, справедливо не только для скоростей, но и для ускорений:

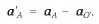
Подставляя в это соотношение выражение для ускорений а_А = - CR_A и a_O'= - CR_O' и используя правило сложения векторов R'_А = R_A — R_O' (рис. 9.5), получим:

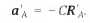
Следовательно, наблюдатель в точке О' будет видеть ту же картину — все частицы материи имеют ускорение, направленное к нему. Ситуация несколько непривычная — ускорение направлено к центру, но центр «виртуальный», им всегда является точка, в которой находится наблюдатель. Такая ситуация концептуально отличается от ньтоновой, в которой предполагается наличие выделенного пространства, общего для всех наблюдателей.

В приведённом выше расчёте распределения ускорений в однородной вселенной не учитывались начальные скорости. Очевидно, что если начальное состояние статично, т, е. скорости нулевые, то вселенная начнёт сжиматься, плотность и ускорения будут расти.

Рассмотрим ситуацию, когда есть некоторые начальные скорости, направленные от наблюдателя (от «центра»). Для сохранения однородности в постановке задачи необходимо, чтобы начальная скорость была пропорциональна расстоянию от наблюдателя:

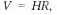
здесь H — коэффициент пропорциональности.

Вселенная будет расширяться, но скорость расширения будет падать. Из-за расширения будет уменьшаться плотность, а, следовательно, и ускорение. Что «пересилит»? Если начальная плотность достаточно велика, или, если угодно, мала начальная скорость, расширение через некоторое время сменится сжатием. При достаточно большой начальной скорости расширение будет продолжаться вечно. Качественно ситуация аналогична, например, рассмотрению стартовавшей с Земли ракеты. При скорости, большей второй космической, ракета может преодолеть притяжение и улететь на бесконечность.

В нашем случае также можно определить критическое распределение скоростей, в данном случае это параметр Н_к, при превышении которого сжатие никогда не наступит. Его значение определяется соотношением:

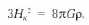
Но точно так же, можно оперировать с критической величиной плотности, рассчитывая её по отношению к параметру Н. Именно так делается при анализе решений Фридмана. Мало того, это соотношение для определения критической плотности полностью совпадает с фридмановским, см. Дополнение 8.

Подведём итог. Оказывается, что законы расширения, определённые Фридманом, полностью совпадают с описанием, представленным только что на основе ньютоновых законов. Таким образом, ещё Ньютон мог представить картину расширения, соответствующую моделям Фридмана. По этому поводу приведём слова Зельдовича: «Величие открытия Фридмана заключается, может быть, не столько в применении общей теории относительности, сколько в отказе от предвзятого представления о стационарности Вселенной».

Объяснение фотометрического парадокса основано на конечности возраста Вселенной. Очень интересно, что такое решение проблемы было предложено задолго до построения ОТО, т. е. конечный возраст Вселенной был просто предположением, плодом интуиции. Скорее всего, приоритет нужно отдать немецкому астроному Иоганну Мёдлеру (1794–1874), заявившему об этом в 1861 году. Математическое изучение этого предположения провёл английский физик Уильям Томсон (1824–1907), более известный как Кельвин. По современным данным возраст Вселенной более 13 млрд лет, следовательно, исключается основное предположение парадокса: бесконечное число звёзд. В реальности их нет дальше границы определённой возрастом Вселенной. Справедливости ради нужно отметить, что это решение проблемы фотометрического парадокса было предложено ещё раньше, и не учёным, а писателем и поэтом Эдгаром По в 1848 году в поэме «Эврика».

Существует ещё один фактор, который снижает яркость неба. Это космологическое красное смещение, о котором речь уже шла.

Но как оказалось, модели, основанные на стандартном (обычном) фридмановском расширении имеют проблемы. Избавились от проблем не релятивистской космологии, зато приобрели новые. Но ничего не поделаешь, в этом и состоит логика развития науки. Итак, фридмановское расширение имеет место тогда, когда пространство заполнено веществом с обычным уравнением состояния, то есть вещество имеет положительное (или нулевое) давление. Получив начальный импульс (что само по себе также является предметом для изучения), планковский «зародыш» далее расширяется по инерции в соответствии с

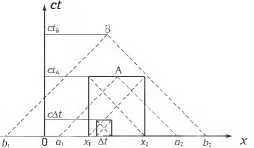
Рис. 9.6. Причинно связанные области и горизонты

решениями Фридмана. Все решения Фридмана имеют степенной по времени характер расширения: a(t) ~ t^x. В зависимости от типа решения (гиперболическое, плоское, замкнутое) и от свойств наполнителя (материи) определяется конкретное значение х, но в любом случае 0 < х < 1, а это означает, что во всех случаях расширение происходит с замедлением. Это взаимное притяжение материи тормозит её разлёт. На настоящий момент весьма точно известны значения важных параметров модели Вселенной. Используя известный закон расширения, мы можем экстраполировать значения этих параметров на ранние времена, сравнимые с планковкими. Проделав это, мы обнаружим некоторые удивительные факты, не имеющие разумного объяснения. Опишем их ниже.

Сначала определим понятие космологического горизонта событий. Пусть в момент времени t = 0 «родилась» вселенная (рис. 9.6). Но для простоты предположим, что эта вселенная не реальная, а «игрушечная», представляет мир Минковского (не расширяющийся и не сжимающийся). Все точки в «начальном» пространстве при t = 0 причинно не связаны. Действительно, они ещё не успели обменяться никакими сигналами, Наблюдатель в любой точке в самый начальный момент ничего не видит из–за того, что никакой свет до него ещё не дошёл. Через момент ∆t появятся области пространства размером ∆х = c∆t, точки которого обменялись сигналами, пунктирные линии на рис. 9.6 обозначают мировые линии световых лучей. Ясно, что со временем такие причинно связанные области растут, на рис. 9.6 область от х₁ до х₂ стала причинно связанной за время t_A. Чем такие области замечательны? Пусть они заполнены каким-то веществом. В силу случайного рождения оно изначально не однородно и не равновесно. Однако, становясь причинно связанными, эти области имеют большие шансы стать однородными и равновесными, поскольку даже крайние точки могли обменяться сигналами. Вернёмся к наблюдателям. С течением времени они будут видеть все большую часть родившегося мира. Наблюдателю в мировой точке А на рис. 9.6 доступна область а₁а₂, а наблюдателю В в более поздний момент времени — уже область b₁b₂.

Граница принципиально наблюдаемой области пространства называется горизонтом событий для данного наблюдателя. На данный момент времени размеры горизонта и причинно связанной области одинаковы по порядку величины. В случае нашей «игрушечной» вселенной с пространством Минковского горизонт в 2 раза больше причинно связанной области на тот же момент времени, как показано на рисунке.

Теперь перейдём к обсуждению вселенной Фридмана. В отличие от «вселенной Минковского» она расширяется. Вспомним, что расширение имеет степенной характер по времени a(t) ~ t^x при 0 < x < 1. Существует ли горизонт событий для такой вселенной? Поведение масштабного фактора a(t) позволяет вычислить расстояние, которое проходит свет за время t, — оно будет пропорционально t. В то же самое время, вселенная Фридмана расширяется с замедлением. Поэтому распространение света «обгоняет рост масштабного фактора», а значит, горизонт событий существует, и в далёком будущем в его пределах окажется любая наперёд заданная частица. Принципиально вселенная Фридмана имеет те же свойства, как и «игрушечная» вселенная Минковского. Размеры горизонта и причинно связанной области одинаковы по порядку величины на каждый момент времени.

Теперь сформулируем проблему горизонта вселенной Фридмана, или её ещё называют проблемой однородности и изотропии. Возраст Вселенной на настоящий момент считается большим 13 млрд лет, отсюда вычисляется современный горизонт, принципиально наблюдаемая область, который имеет порядок 10²⁸ см. Возвращаясь в планковскую эпоху t = 10–4³ с, используя закон расширения Фридмана, получим, что тогда наша современная область наблюдений имела размеры порядка 10–3см. Такой объём содержал 10⁹⁰(!) планковских областей. В планковскую эпоху каждая такая область только что «родилась» и не имела возможности обменяться сигналами с остальными. То есть все они между собой причинно не связаны. Однако, как говорилось, наблюдаемая часть Вселенной весьма однородна и изотропна. Но это означает, что все 10⁹⁰ начальных планковских областей должны быть одинаковы. В силу неизвестной нам физики можно предположить, что «внутри себя» планковская область однородна и изотропна. Но это же утверждение для 10⁹⁰ начальных планковских областей невероятно и в рамках фридманов кой космологии объяснения не имеет.

Описание проблемы горизонта на примере план ковких масштабов, хотя и выглядит впечатляюще, кому-то покажется оторванным от реальности. Часто, чтобы её представить, обращаются к вполне подтверждённым наблюдениям. Для этого мы забегаем вперёд, несколько предваряя рассказ об эволюции материи во Вселенной. Важным периодом является эпоха рекомбинации водорода. С расширением Вселенная остывает, и, естественно, состояние материи меняется. Был период, когда она была заполнена равновесным газом протонов и электронов со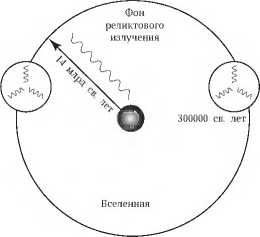

Рис. 9.7. Проблема изотропии реликтового излучения

вместно с электромагнитным излучением (фотонами). Когда температура достаточно понизилась, это было через 300000 лет после Большого взрыва, отдельные протоны и электроны объединились в атомы водорода (момент рекомбинации). Среда стала прозрачной для электромагнитного излучения, которое далее расширяется независимо, Как следствие, в наше время это излучение (реликтовое) наблюдается очень остывшим.

Обратимся к рис. 9.7. Реликтовое излучение приходит к нам с огромного расстояния около 14 млрд световых лет (большой круг). Однако когда это излучение начало свой путь, возраст Вселенной был, как мы отметили, 300 000 лет и за это время обменяться сигналами (пусть световыми) могли небольшие области (маленькие окружности). Два маленьких круга на рисунке никак не могли обменяться сигналами, т, е. они причинно не связаны, Поэтому нет оснований для того, чтобы они имели одинаковые характеристики, скорее, наоборот. Однако реликтовое излучение, которое мы наблюдаем со всей большой сферы, в высшей степени изотропно] Это и есть проблема однородности и изотропии в иной иллюстрации.

Обсудим другую проблему. Каждый из трёх типов расширения глобального пространства Вселенной определяется средней плотностью вещества, заполняющего это 3–мерное пространство. Плоскому случаю соответствует критическая плотность. Если плотность меньше — будет гиперболическое пространство, если больше — замкнутое. Важно иметь в виду, что для каждого момента в эволюции критическая плотность имеет разное значение. Так вот, наблюдения показывают, что с очень высокой точностью современная плотность всего вещества во Вселенной близка к критической, то есть мы живём фактически в плоском пространстве, или (что то же самое) в пространстве с огромным радиусом кривизны. Возвращаясь в планковскую эпоху, получим, что тогда плотность должна была быть близкой к критической с невероятной точностью 10⁶⁰! Почему так? Объяснить этот факт в рамках обычной фридмановской модели тоже не получается. Это вторая проблема и она называется проблемой плоскостности.

Пойдём дальше. Когда говорилось об однородности — это означало, что видимая часть Вселенной мысленно разбивалась на «кубики», очень мелкие по сравнению со всем наблюдаемым объёмом. Однородность означает, что массы всех таких кубиков одинаковы. Условно говоря, в каждом кубике одинаковое количество галактик. Продолжим операцию. Теперь каждый из уже имеющихся кубиков разобьём на ещё более мелкие по отношению к исходным. Тогда обнаружится, что какой-то кубик второго порядка малости содержит отдельные галактики, какой-то скопления и даже сверхскопления галактик, а какие-то кубики останутся совсем пустыми. То есть обнаружится, что на меньших масштабах Вселенная неоднородна.

Распределение сверхскоплений, скоплений галактик и самих галактик называется крупномасштабной космологической структурой, Известно, что она развивается из флуктуаций плотности, возникших во времена, близкие к планковским. Если мы хотим получить в результате обычного фридмановского расширения ту структуру, которую имеем сейчас, и которая достаточно хорошо изучена, то исходные возмущения план ков с кой эпохи должны быть не произвольными, а очень специфичными. Но для этого нет веских оснований, и это третья проблема — проблема первичных флуктуаций плотности.