Книга: Мир в ореховой скорлупке [илл. книга-журнал]
Назад: Глава 1 Краткая история относительности
Дальше: Глава 3 Мир в ореховой скорлупке
Глава 2
Форма времени
О том, что теория относительностипридает времени форму и как это можно примиритьс квантовой теорией

Что такое время? Тот ли оно вечно катящийся поток, что смывает все наши мечты, как говорится в старинном псалме? Или это колея железной дороги? Возможно, у нее есть петли и кольца, так что вы можете, продолжая движение вперед, вернуться к станции, которую уже миновали (рис. 2.1).
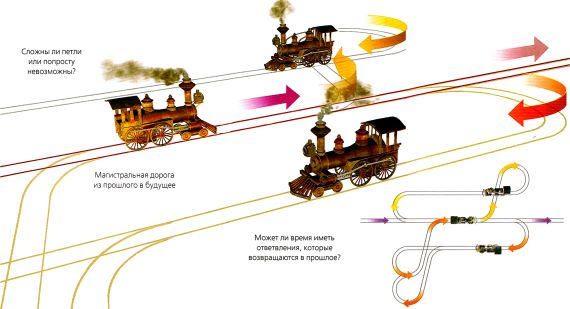
Рис. 2.1 Модель времени как железнодорожного пути
Что есть время? Представляет ли оно собой единственную магистральную колею с односторонним движением — из прошлого в будущее — или возможны уходящие назад петли, которые вновь соединяются с основной магистралью на уже пройденном составом разъезде?
Чарльз Лэмб в XIX веке писал: «Ничто не озадачивает меня так, как время и пространство. И ничто не беспокоит меня меньше, чем время и пространство, поскольку я никогда не думаю о них». Большинство из нас почти никогда не беспокоится о времени и пространстве, чем бы они ни были; но все мы иногда задумываемся, что же такое время, откуда оно взялось и куда нас ведет.
Любая разумная научная теория, касается ли она времени или любого другого предмета, должна, по моему мнению, основываться на наиболее работоспособной философии науки — позитивистском подходе, который был разработан Карлом Поппером и другими. Согласно этому образу мысли научная теория — это математическая модель, которая описывает и систематизирует производимые нами наблюдения. Хорошая теория описывает широкий круг явлений на базе нескольких простых постулатов и дает ясные предсказания, которые можно проверить. Если предсказания согласуются с наблюдениями, теория выдерживает испытание, хотя никогда нельзя будет доказать ее правильность. С другой стороны, если наблюдения не соответствуют предсказаниям, придется либо отбросить, либо модифицировать теорию. (По крайней мере, предполагается, что так должно быть. На практике люди часто задаются вопросом о точности наблюдений, а также надежности и моральном облике тех, кто их выполнял.) Если принимать позитивистские принципы, как это делаю я, то невозможно сказать, что в действительности представляет собой время. В наших силах лишь описать то, что, как мы знаем, является очень хорошей математической моделью для времени, и перечислить, какие предсказания она позволяет сделать.
Исаак Ньютон дал нам первую математическую модель времени и пространства в своем труде «Principia Mathematica» («Математические начала натуральной философии»), опубликованном в 1687 г. Ньютон занимал в Кембридже кресло Лукасовского профессора математики, которое ныне занимаю я, правда, в его время оно не имело электронного управления.

Исаак Ньютон опубликовал свою математическую модель времени и пространства более 300 лет назад
В ньютоновской модели время и пространство были тем фоном, на котором события разворачивались, но который они не затрагивали. Время было отделено от пространства и рассматривалось как единственная линия, железнодорожная колея, бесконечная в обоих направлениях (рис. 2.2).
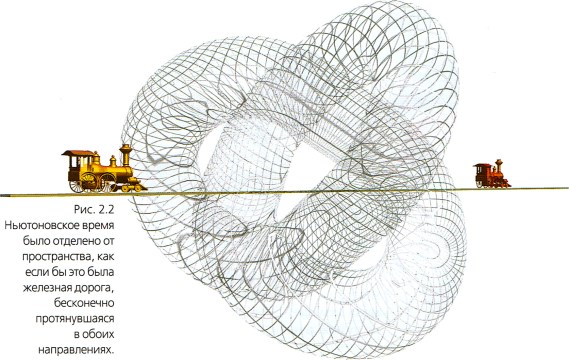
Само время считалось вечным в том смысле, что оно существовало и будет существовать всегда. В противоположность этому большинство людей полагало, что физический мир был создан в более или менее современном виде всего несколько тысяч лет назад. Это беспокоило философов, таких как немецкий мыслитель Иммануил Кант. Если Вселенная действительно создана, то зачем нужно было ждать целую вечность перед ее созданием? С другой стороны, если Вселенная существует вечно, то почему все, что должно произойти, еще не случилось, иначе говоря, почему история еще не закончилась? И в частности, почему Вселенная еще не достигла термодинамического равновесия с повсеместно одинаковой температурой?
Кант назвал эту проблему «антиномией чистого разума», поскольку она казалась ему логическим противоречием; она не имела решения. Но это было противоречием только в контексте ньютоновской математической модели, в которой время представляло собой бесконечную линию, не зависящую от того, что случается во Вселенной. Между тем, как было показано в главе 1, Эйнштейн в 1915 г. выдвинул совершенно новую математическую модель — общую теорию относительности. За годы, прошедшие с появления статьи Эйнштейна, мы добавили к ней кое-какие детали, но в целом наша модель по-прежнему основана на том, что предложил Эйнштейн. В этой и последующих главах будет описано, как развивались наши представления после публикации революционной статьи Эйнштейна. Это была история успешной работы большого числа людей, и я горжусь, что смог внести в нее свой небольшой вклад.
Общая теория относительности объединяет временное измерение с тремя измерениями пространства и образует то, что мы называем пространством-временем (рис. 2.3). Теория включает действие гравитации, утверждая, что наполняющие Вселенную вещество и энергия искривляют и деформируют пространство-время так, что оно перестает быть плоским. Объекты в пространстве-времени стремятся двигаться по прямым линиям, но поскольку оно само искривлено, их пути выглядят изогнутыми. Они движутся так, будто на них действует гравитационное поле.

Рис. 2.3. Форма и направление времени
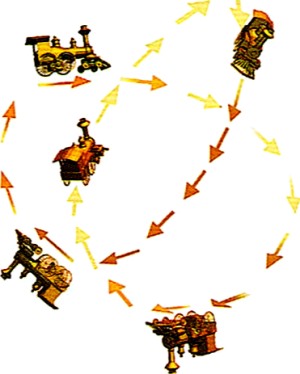
Теория относительности Эйнштейна, которая согласуется с большим числом экспериментов, говорит, что время и пространство неразделимо переплетены. Невозможно искривить пространство, не затрагивая времени. Поэтому время имеет форму. Однако оно все равно движется в одном направлении, как паровозы на этом рисунке.
В качестве грубой аналогии, которую не следует воспринимать буквально, представьте себе лист резины. Можно положить на него большой мяч, который будет изображать Солнце. Вес мяча продавит лист и вызовет его искривление вблизи Солнца. Если теперь запустить по листу маленький шарик, тот не будет катиться прямо от одного края к другому, а вместо этого станет двигаться вокруг большой массы, подобно тому как планеты обращаются вокруг Солнца (рис. 2.4).

Рис. 2.4 Аналогия с резиновым листом
Большой шар в центре представляет массивное тело, например звезду. Под действием веса тела лист вблизи него искривляется. Шарик, катящийся по листу, отклоняется этой кривизной и двигается вокруг большого шара, подобно тому как планеты в гравитационном поле звезды обращаются вокруг нее.
Эта аналогия неполна, поскольку в ней искривляется только двумерное сечение пространства (поверхность резинового листа), а время остается вовсе незатронутым, как в ньютоновской механике. Тем не менее в теории относительности, которая согласуется с большим числом экспериментов, время и пространство неразрывно связаны друг с другом. Нельзя добиться искривления пространства, не вовлекая также и время. Получается, что время имеет форму. Благодаря искривлениям пространство и время в общей теории относительности превращаются из пассивного фона, на котором развиваются события, в динамических участников происходящего. В теории Ньютона, где время существует независимо от всего остального, можно спросить: что делал Бог до того, как Он создал Вселенную? Как говорил Августин Блаженный, не следует сводить эту тему к шуткам по примеру человека, сказавшего: «Он готовил ад для чрезмерно любопытных». Это слишком серьезный вопрос, над которым люди размышляли веками. Согласно Блаженному Августину, перед тем как Бог создал небеса и землю, Он вообще ничего не делал. На самом деле это очень близко к современным представлениям.
Августин Блаженный.
Рисунок из его книги «О граде Божьем» («De Civitate Dei»), XII в. Библиотека «Лоренциана», Флоренция. Этот мыслитель, живший в V в. н. э., считал, что времени не существовало до сотворения мира.
С одной стороны, в общей теории относительности время и пространство не существуют независимо от Вселенной и друг от друга. Они определяются посредством измерений, выполняемых внутри Вселенной, например по числу колебаний кварцевого кристалла в часах или по длине линейки. И совершенно ясно, что раз время определено подобным образом внутри Вселенной, то у него должны быть минимальный и максимальный отсчеты, иными словами, начало и конец. Не имеет никакого смысла спрашивать, что случилось до начала или после конца, поскольку нельзя указать таких моментов времени.
По-видимому, важно понять, действительно ли математическая модель общей теории относительности предсказывает, что Вселенная и само время должны иметь начало и конец. Общее для физиков-теоретиков, включая Эйнштейна, предубеждение состояло в том, что время должно быть бесконечным в обоих направлениях. С другой стороны, имелись неудобные вопросы о сотворении мира, которые, как казалось, находятся вне компетенции науки. Такие решения уравнений Эйнштейна, в которых время имело начало или конец, были известны, но они получались в очень специальных высокосимметричных частных случаях. Считалось, что для реального тела, коллапсирующего под действием собственной гравитации, давление и боковые скорости должны предотвратить падение всего вещества в одну точку, в которой плотность возрастает до бесконечности. Аналогично, если проследить назад во времени расширение Вселенной, могло оказаться, что материя вовсе не была выброшена из одной точки с бесконечной плотностью, называемой сингулярностью, которая может служить началом или концом времени.
В 1963 г. двое советских ученых, Евгений Лифшиц и Исаак Халатников, объявили: они располагают доказательством того, что все решения уравнений Эйнштейна с сингулярностью имеют особое распределение материи и скоростей. Вероятность того, что решение, представляющее нашу Вселенную, имеет такое специальное распределение, была практически нулевой. Почти все решения, которые могут соответствовать нашей Вселенной, должны обходиться без сингулярности с бесконечной плотностью. Эре, в течение которой Вселенная расширяется, должна была предшествовать фаза сжатия, во время которой вещество падало само на себя, но избегало столкновения, разлетаясь вновь в современной фазе расширения. Если бы все обстояло именно так, то время могло бы длиться вечно — от бесконечного прошлого до бесконечного будущего.
Не все согласились с аргументами Аифшица и Халатникова. Мы с Роджером Пенроузом применили другой подход, основанный не на детальном изучении решений, а на глобальной структуре пространства-времени. В общей теории относительности пространство-время искривляется не только находящимися в нем массивными объектами, но также энергией. Энергия всегда положительна, поэтому она всегда придает пространству-времени такую кривизну, которая сближает лучи друг с другом.
Рассмотрим световой конус прошлого (рис. 2.5), представляющий собой пути сквозь пространство-время лучей света далеких галактик, приходящих к нам в настоящее время. На диаграмме, где время направлено вверх, а пространство — в стороны, получается конус с вершиной, в которой находимся мы.
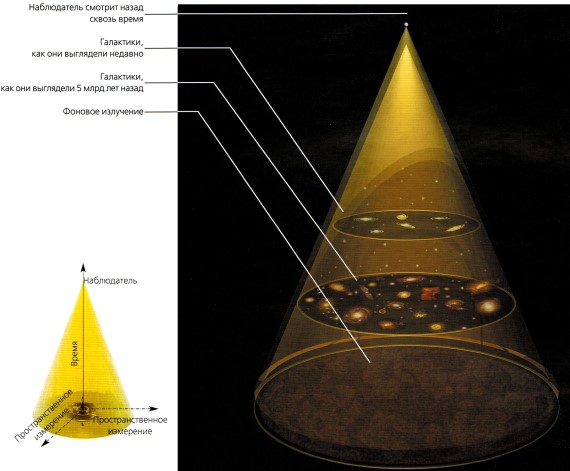
Рис. 2.5
Когда мы смотрим на далекие галактики, то видим Вселенную такой, какой она была в прошлом, поскольку свет распространяется с конечной скоростью. Если мы представим время вертикальной осью, а два пространственных измерения — горизонтальными осями, то свет, который сейчас достигает нас в верхней точке, движется к нам по поверхности конуса.
По мере движения в прошлое, от вершины вниз по конусу, мы видим галактики во все более и более раннее время. Поскольку Вселенная расширяется и все объекты становятся намного ближе друг к другу, наш взгляд проходит через области со все большей плотностью материи. Мы наблюдаем слабый фон микроволнового излучения, который приходит к нам вдоль светового конуса прошлого из намного более раннего времени, когда Вселенная была значительно плотнее и горячее, чем сейчас. Настраивая приемник на разные частоты микроволн, мы можем измерить спектр излучения (распределение энергии по частотам). Мы обнаружили спектр, который характерен для излучения тела с температурой 2,7 градуса выше абсолютного нуля. Это микроволновое излучение малопригодно для размораживания пиццы, но сам факт, что его спектр столь точно соответствует излучению тела с температурой 2,7 градуса Кельвина, говорит о том, что оно должно приходить из области, непрозрачной для микроволн (рис. 2.6).
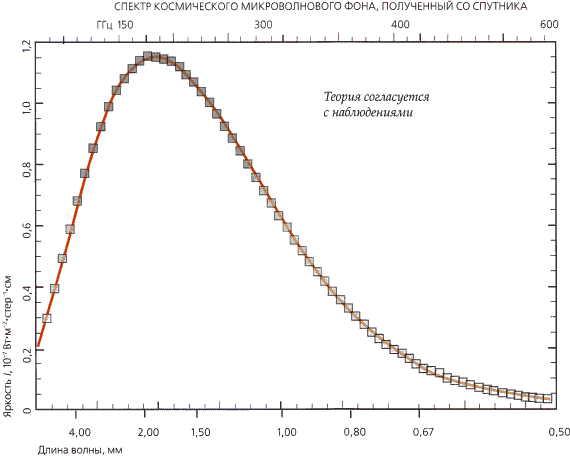
Рис. 2.6 Измерение спектра микроволнового фона
Спектр космического микроволнового излучения, то есть распределение его интенсивности по частотам, характерен для нагретого тела. Чтобы излучение пришло в тепловое равновесие, оно должно многократно рассеиваться на веществе. Это указывает на то, что в световом конусе нашего прошлого должно было быть достаточно вещества, чтобы вызвать его стягивание.
Итак, можно заключить, что наш световой конус прошлого, если проследить его назад, проходит через определенное количество вещества. Этого количества достаточно для искривления пространства-времени таким образом, чтобы лучи света в нашем световом конусе изогнулись навстречу друг другу (рис. 2.7).

Рис. 2.7 Искривленное пространство-время
Поскольку гравитация вызывает притяжение, вещество всегда искривляет пространство-время так, что лучи света изгибаются один к другому.
По мере движения назад во времени поперечное сечение светового конуса прошлого достигнет максимального размера и вновь начнет уменьшаться. Наше прошлое имеет грушевидную форму (рис. 2.8).
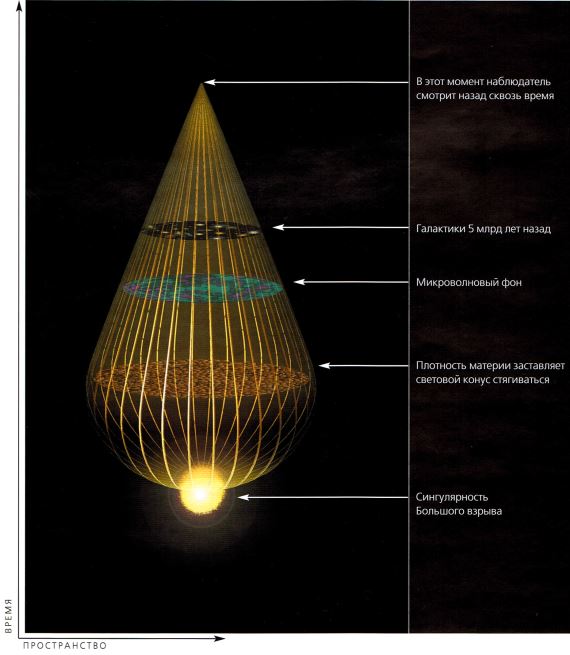
Рис. 2.8. Грушевидное время
Если проследить световой конус нашего прошлого назад во времени, в ранней Вселенной он стянется под воздействием вещества. Вся Вселенная, которая доступна нашим наблюдениям, содержится в области, границы которой сжимаются до нуля в момент Большого взрыва. Это будет сингулярность, место, где плотность материи должна возрастать до бесконечности, а классическая общая теория относительности перестает работать.
Следуя дальше вдоль светового конуса нашего прошлого, мы обнаружим, что положительная плотность энергии вещества заставляет лучи света загибаться друг к другу еще сильнее. Поперечное сечение светового конуса стягивается к нулевому размеру за конечное время. Это означает, что все вещество внутри светового конуса прошлого загнано в область, граница которой стягивается к нулю. Неудивительно, что мы с Пенроузом смогли доказать: в математической модели общей теории относительности время должно иметь начало в виде того, что мы называем Большим взрывом. Аналогичные аргументы показывают, что время будет иметь конец, когда звезда или галактика коллапсирует под действием собственного тяготения и образует черную дыру. Мы обошли парадокс чистого разума Канта, отбросив его неявное предположение о том, что время имеет смысл независимо от Вселенной. Наша статья, доказывающая, что время имело начало, заняла второе место на конкурсе, организованном Фондом изучения гравитации (Gravity Research Foundation) в 1968 г., и мы с Роджером поделили щедрый приз в 300 долларов. Не думаю, что в том году какая-либо другая из поданных на конкурс работ имела столь непреходящую ценность.
Наша статья вызвала разнообразные отклики. Многих физиков она огорчила, но зато обрадовала тех религиозных лидеров, которые верили в акт Творения — здесь было его научное доказательство. Между тем Лифшиц и Халатников оказались в неловком положении. Они не могли ни оспорить математическую теорему, которую мы доказали, ни признать в условиях советской системы, что они ошиблись, а западные ученые оказались правы. И все же они сохранили лицо, найдя более общее семейство решений с сингулярностью, которое не было специальным в том смысле, в котором это относилось к их прежним решениям. Последнее позволило им объявить сингулярности, а также начало и конец времени советским открытием.
Большинство физиков по-прежнему инстинктивно не любят мысль о том, что время имеет начало или конец. Поэтому они отмечают, что данная математическая модель не может считаться хорошим описанием пространства-времени вблизи сингулярности. Причина состоит в том, что общая теория относительности, которая описывает силу гравитации, является, как отмечалось в главе 1, классической теорией и не учитывает неопределенности квантовой теории, которая управляет всеми другими известными нам силами. Эта несовместимость не играет никакой роли в большей части Вселенной на протяжении большей части времени, поскольку масштаб, в котором искривляется пространство-время, очень велик, а масштаб, в котором существенны квантовые эффекты, очень мал. Но вблизи сингулярности эти два масштаба становятся сравнимыми и квантовые гравитационные эффекты должны становиться существенными. Поэтому в теореме о сингулярности мы с Пенроузом в действительности установили, что наша классическая область пространства-времени ограничена со стороны прошлого и, возможно, со стороны будущего областями, в которых существенны эффекты квантовой гравитации. Чтобы понять происхождение и судьбу Вселенной, нам необходима квантовая теория гравитации, и она будет предметом большей части этой книги.
Квантовые теории для таких систем, как атомы, с конечным числом частиц, были сформулированы в 1920-х гг. Гейзенбергом, Шрёдингером и Дираком. (Дирак также занимал когда-то мое кресло в Кембридже, но и при нем оно не было моторизовано.) Однако попытка распространить квантовые идеи на максвелловское (электромагнитное) поле, которое описывает электричество, магнетизм и свет, столкнулась с трудностями.
Принцип неопределенности


Важным шагом к открытию квантовой теории стало выдвинутое в 1900 г. Максом Планком предположение, что свет всегда существует в форме небольших пакетов, которые он назвал квантами. Но хотя квантовая гипотеза Планка полностью объяснила наблюдаемый характер излучения горячих тел, полный масштаб ее следствий не осознавался до середины 1920-х гг., когда немецкий физик Вернер Гейзенберг сформулировал свой знаменитый принцип неопределенности. Он заметил, что согласно гипотезе Планка чем точнее мы пытаемся измерить положение частицы, тем менее точно можем измерить ее скорость, и наоборот.
Более строго, он показал, что неопределенность положения частицы, умноженная на неопределенность ее импульса, всегда должна быть больше постоянной Планка, численное значение которой тесно связано с энергией, переносимой одним квантом света.
Уравнение неопределенности Гейзенберга

Можно представлять себе максвелловское поле состоящим из волн разной длины (длина волны — расстояние от одного ее гребня до другого). В волне поле колеблется от одного значения к другому, подобно маятнику (рис. 2.9).
Поле Максвелла
В 1865 г. британский физик Джеймс Клерк Максвелл объединил все известные законы электричества и магнетизма. Теория Максвелла базируется на существовании «полей», которые передают действие из одного места в другое. Он догадался, что поля, которые передают электрические и магнитные возмущения, представляют собой динамические сущности: они могут колебаться и перемещаться в пространстве. Максвелловский синтез электромагнетизма можно выразить всего двумя уравнениями, которые описывают динамику этих полей. Он сам вывел первое важнейшее следствие своих уравнений — то, что электромагнитные волны всех частот распространяются в пространстве с одной и той же фиксированной скоростью, со скоростью света.
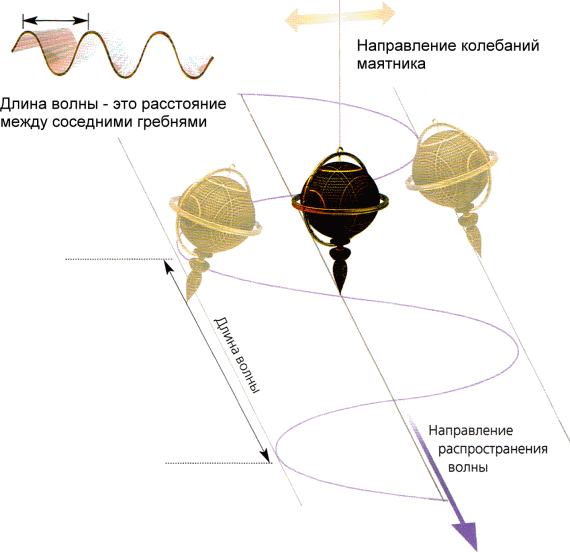
Рис. 2.9 Движение волны и колебания маятника
Электромагнитное излучение распространяется сквозь пространство как волна, в которой электрическое и магнитное поля колеблются, подобно маятнику, в направлении, поперечном движению самой волны. Излучение может состоять из колебаний полей с разными длинами волн.
Согласно квантовой теории основное состояние маятника, то есть состояние с наименьшей энергией, — это вовсе не покой в самой низкоэнергетической точке в направлении прямо вниз. В данном случае он имел бы одновременно определенное положение и определенную скорость, равную нулю.
Это нарушало бы принцип неопределенности, который запрещает точное измерение положения и скорости в один и тот же момент времени. Неопределенность положения, умноженная на неопределенность импульса, должна быть больше некоторой величины, известной как постоянная Планка — ее численное значение слишком длинное, чтобы его здесь выписывать, поэтому мы будем обозначать ее символом ħ.
Так что основное состояние маятника, или состояние с наименьшей энергией, имеет ненулевую энергию в противоположность тому, что можно было ожидать. Оказывается, даже в основном состоянии маятник, как и любая колебательная система, должен совершать минимального размера флуктуации, называемые нулевыми колебаниями. Это означает, что маятник необязательно будет указывать прямо вниз, есть также вероятность обнаружить его отклоненным на небольшой угол от вертикали (рис. 2.10). Подобным образом даже в вакууме, то есть в состоянии наименьшей энергии, волны максвелловского поля не затухают до нуля, но могут иметь небольшие размеры. Чем выше частота (количество колебаний в минуту) маятника или волны, тем больше энергия основного состояния.
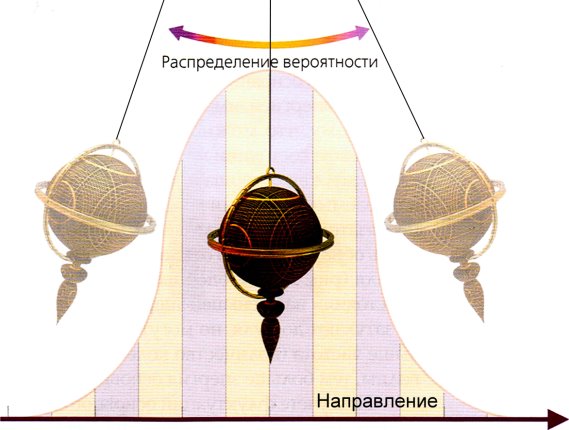
Рис. 2.10 Маятник и распределение вероятности
Согласно принципу Гейзенберга маятник не может висеть, указывая строго вниз, и обладать при этом нулевой скоростью. Квантовая теория предсказывает, что даже в состоянии наименьшей энергии он должен испытывать минимальные флуктуации.
Это означает, что положение маятника должно задаваться распределением вероятности. Если он находится в основном состоянии, то с наибольшей вероятностью будет указывать прямо вниз, но имеется также вероятность обнаружить его под небольшим углом к вертикали.
При учете флуктуаций основного состояния в максвелловском поле электрона его видимые масса и заряд оказываются бесконечными, что, конечно, не соответствует наблюдениям. Однако в 1940-х гг. физики Ричард Фейнман, Джулиан Швингер и Синъитиро Томонага разработали согласованный метод устранения, или «вычитания», этих бесконечностей, чтобы иметь дело только с конечными наблюдаемыми значениями масс и энергий. И все же флуктуации основного состояния вызывают небольшие эффекты, которые можно измерить и которые подтверждаются экспериментом. Похожие схемы избавления от бесконечностей работают и для полей Янга — Миллса в теории, которую разработали Чженьнин Янг и Роберт Миллс. Теория Янга — Миллса — это расширение теории Максвелла, которое описывает действие двух других сил, называемых слабым и сильным ядерными взаимодействиями. Однако в случае квантовой теории гравитации флуктуации основного состояния вызывают гораздо более серьезные эффекты. Здесь тоже каждая длина волны имеет свою энергию основного состояния.
Поскольку нет ограничений на то, сколь короткими могут быть длины волн максвелловского поля, то в любой области пространства-времени содержится бесконечное число различных волн и бесконечное количество энергии основного состояния. А вследствие того что плотность энергии, как и вещество, служит источником гравитации, эта бесконечная плотность энергии должна означать, что у Вселенной достаточно тяготения, чтобы свернуть пространство-время в одну точку, чего, однако, очевидно, не происходит.
Можно надеяться разрешить проблему этого внешнего противоречия между наблюдениями и теорией, заявив, что флуктуации основного состояния не влияют на гравитацию, но это не работает. Энергию флуктуаций основного состояния можно обнаружить благодаря эффекту Казимира. Если взять пару металлических пластин и поместить их параллельно друг другу на небольшом расстоянии друг от друга, то число волн различной длины, которые помещаются между пластинами, слегка уменьшится по сравнению с их числом вовне. Это означает, что между пластинами плотность энергии флуктуаций основного состояния хотя и останется бесконечной, окажется меньше плотности энергии вовне на некоторую конечную величину (рис. 2.11). Данная разница в плотности энергии приводит к появлению силы, которая прижимает пластины друг к другу, и эту силу можно наблюдать экспериментально. Силы в общей теории относительности являются источником гравитации наряду с веществом, так что было бы непоследовательным игнорировать гравитационный эффект этой разницы в энергии.
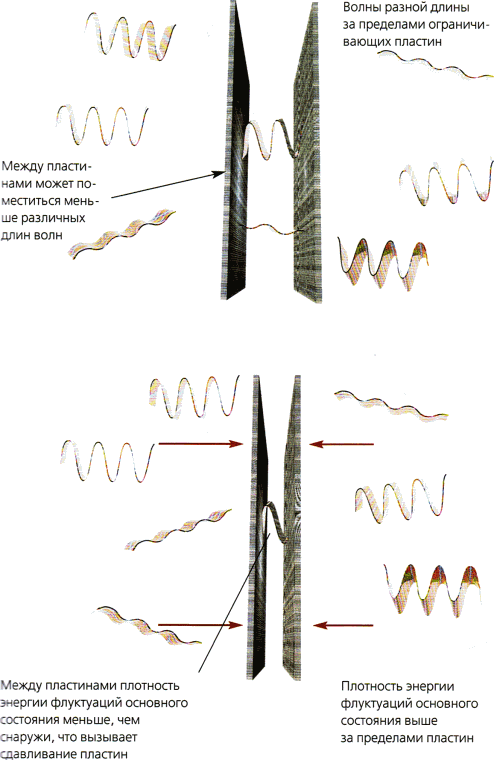
Рис. 2.11 Эффект Казимира
Существование флуктуаций основного состояния было подтверждено экспериментально в эффекте Казимира, который проявляется как небольшая сила, действующая между параллельными металлическими пластинами.
Другой подход к решению рассматриваемой проблемы — попробовать задействовать космологическую постоянную, такую как ввел Эйнштейн в попытке получить стационарную Вселенную. Если эта постоянная имеет бесконечное отрицательное значение, она может в точности скомпенсировать бесконечное положительное значение энергии основного состояния в свободном пространстве, но такая космологическая постоянная кажется слишком искусственным предположением, и к тому же ее величина должна быть подогнана с невероятной точностью.
К счастью, в 1970-х гг. был открыт совершенно новый тип симметрии, который обеспечил естественный физический механизм сокращения бесконечностей, появляющихся из флуктуаций основного состояния. Суперсимметрия — это свойство наших современных математических моделей, которое можно описывать разными способами. Один из подходов состоит в том, чтобы объявить пространство-время имеющим дополнительные измерения помимо тех, с которыми мы знакомы на практике. Они называются размерностями Грассмана, поскольку отсчеты, производимые вдоль них, описываются грассмановскими, а не обычными действительными числами. Обычные числа коммутативны; не имеет значения, в каком порядке вы их перемножаете: 6 умножить на 4 — это то же самое, что 4 умножить на 6. Однако грассмановские величины антикоммутативны: х умножить на у равно — у умножить на х.
Обычные числа А х В = В х А
Грассмановские числа А х В = — В х А
Суперсимметрию впервые стали применять для исключения бесконечностей в материальных полях и полях Янга-Миллса в пространстве-времени, все измерения которого, как обычные, так и грассмановские, были плоскими, а не искривленными. Однако было естественно распространить подход на случай, когда те и другие измерения являются искривленными. Это привело к появлению ряда теорий, называемых супергравитацией, с разной степенью суперсимметрии. Одно из следствий суперсимметрии состоит в том, что у любого поля или частицы должны быть «суперпартнер» со спином либо на 1/2 больше, либо на 1/2 меньше (рис. 2.12).
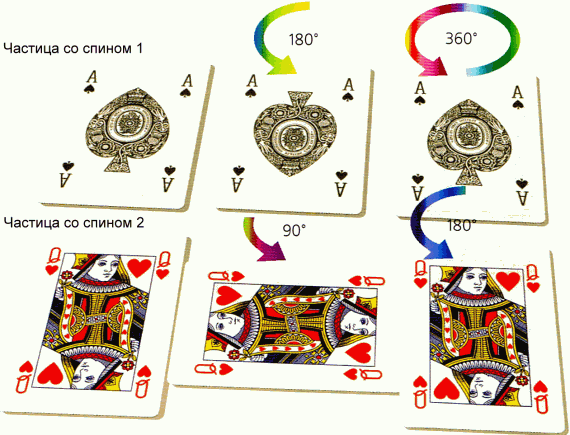

Рис 2.12 Спин
Все частицы обладают свойством, называемым спином, которое проявляется в том, что частицы по-разному выглядят с разных направлений. Это можно проиллюстрировать на примере колоды карт. Возьмем для начала пикового туза. Он выглядит неизменно только при полном обороте — на 360°. Поэтому говорят, что у него спин 1.
С другой стороны, у червовой дамы две головы. И потому она не меняется при повороте на 180°.
Про это говорят: спин 2. Подобным образом можно представить себе объекты со спином 3 и больше, которые не меняются при повороте на меньшие доли полного оборота.
Чем больше спин, тем меньшая доля оборота нужна, чтобы частица в результате осталась неизменной. Но удивительно, что существуют частицы, которые остаются неизменными только после двух полных оборотов. О таких говорят, что они имеют спин 1/2.
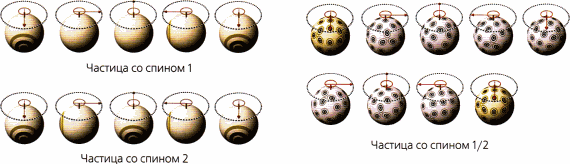
Энергии основного состояния бозонов — полей с целочисленным спином (0,1, 2 и т. д.) — положительны. С другой стороны, энергии основного состояния фермионов — полей, спин которых выражается полуцелыми числами (1/2, 3/2 и т. д.), — отрицательны. Поскольку имеется одинаковое число бозонов и фермионов, крупнейшие бесконечности в теориях супергравитации сокращаются (рис. 2.13).

Рис 2.13 Суперпартнеры
Все известные частицы во Вселенной принадлежат к одной из двух групп: фермионам или бозонам.
Фермионы — это частицы с полуцелым спином (например, 1/2), из них состоит обычное вещество. Энергии их основного состояния отрицательны.
Бозоны — это частицы с целым спином (0, 1, 2 и т. п.). Они связаны с силами, которые действуют между фермионами, например с гравитационным взаимодействием и светом. Энергии их основного состояния положительны.
Теория супергравитации предполагает, что каждый фермион и каждый бозон имеют суперпартнера со спином, который либо на 1/2 больше, либо на 1/2 меньше спина самой частицы. Например, фотон (который является бозоном) имеет спин, равный 1. Его энергия основного состояния положительна. Суперпартнером фотона является фотино — фермион со спином 1/2. Поэтому его энергия основного состояния отрицательна.
В этой супергравитационной схеме мы получаем равное число бозонов и фермионов. Поместив энергии основного состояния бозонов на положительную чашу весов, а энергии фермионов — на отрицательную, мы увидим, что они компенсируют друг друга, устраняя самые большие бесконечности.
Модели поведения частиц
1. Если точечные частицы действительно представляют собой дискретные объекты наподобие бильярдных шаров, тогда при столкновении они должны отклоняться и переходить на новые траектории.
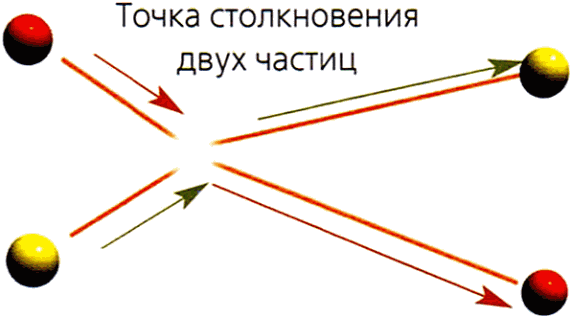
2. Вот что происходит при взаимодействии двух частиц, хотя эффект может быть и более впечатляющим.

3. Квантовая теория поля показывает, как сталкиваются две частицы, подобные электрону и его античастице, позитрону. Они на короткий момент аннигилируют друг с другом в яркой вспышке, порождая фотон, а он затем высвобождает энергию, порождая другую электрон-позитронную пару. Но это выглядит так, будто частицы просто отклонились, перейдя на новые траектории.
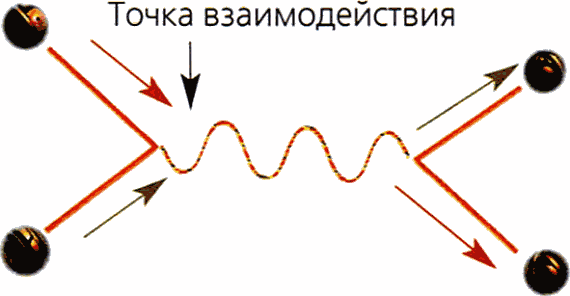
4. Если частицы являются не безразмерными точками, а одномерными замкнутыми струнами, которые колеблются как электрон и позитрон, тогда при столкновении и аннигиляции они порождают новую струну с другой формой колебаний. Высвобождая энергию, она делится на две струны, продолжающие движение по новым траекториям.
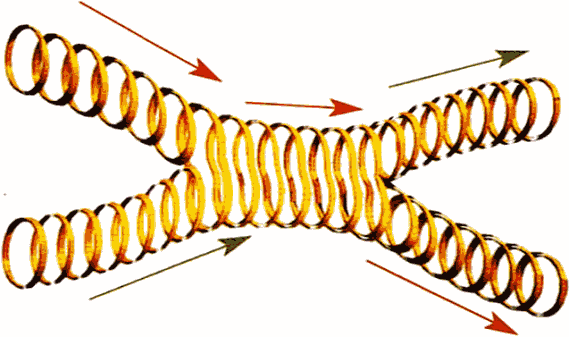
5. Если эти исходные струны рассматривать не в дискретные моменты, а на протяжении непрерывной, разворачивающейся во времени истории, то струны будут выглядеть как мировые поверхности.
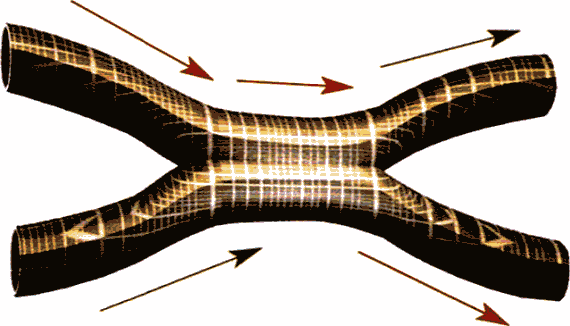
Не исключена, правда, возможность, что могут оставаться меньшие, но по-прежнему бесконечные величины. Никому пока не хватило упорства провести вычисления и выяснить, действительно ли эти теории полностью конечны.
По существующим оценкам, усердному студенту на это потребовалось бы лет двести, и потом неясно, как убедиться, что он не допустил ошибки уже на второй странице. Тем не менее вплоть до 1985 г. специалисты в основном верили, что большинство суперсимметричных теорий супергравитации должны быть свободны от бесконечностей.
А потом мода неожиданно изменилась. Было объявлено, что нет оснований полагать, будто теории супергравитации не содержат бесконечностей, и это привело к тому, что их стали считать безнадежно дефектными. Зато было провозглашено, что концепция, получившая название суперсимметричной теории струн, — единственное, что способно соединить гравитацию с квантовой теорией. Струны в данной теории, подобно тем, что встречаются обыденной жизни, являются одномерными объектами. У них есть только длина. Струны в теории струн движутся на фоне пространства-времени, а их колебания интерпретируются как частицы (рис. 2.14).
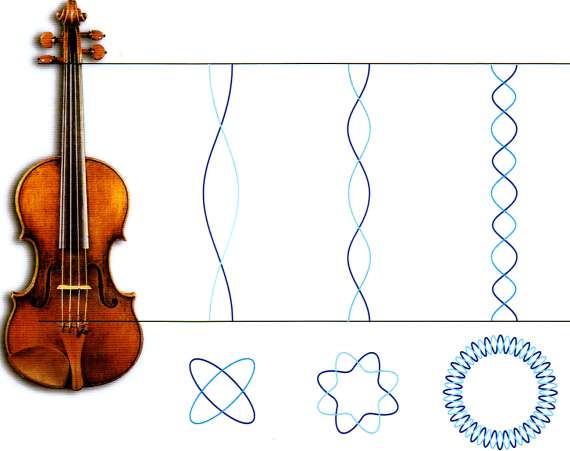
Рис. 2.14. Колебания струн
В теории струн фундаментальные объекты не частицы, занимающие единственную точку в пространстве, а одномерные струны. Эти струны могут иметь концы или замыкаться на себя, образуя петли. В точности как струны скрипки, они могут поддерживать разные режимы колебаний или резонансные частоты, длины волн которых целое число раз укладываются между концами струны.
Но если разные частоты колебаний скрипичных струн порождают разные музыкальные тона, различные режимы колебаний в теории струн соответствуют разным массам и зарядам, что интерпретируется как различные фундаментальные частицы. Грубо говоря, чем короче длина волны колебания струны, тем больше масса частицы.
Если струны обладают грассмановскими измерениями наряду с обычными, их колебания будут соответствовать бозонам и фермионам. В этом случае положительные и отрицательные энергии основных состояний в точности сокращаются, так что не остается никаких бесконечностей, даже малого порядка. Суперструны, как было объявлено, представляют собой Теорию Всею.
Историкам науки в будущем наверняка будет интересно построить график колебания пристрастий физиков-теоретиков. Струны безраздельно властвовали несколько лет, а супергравитация была низведена до статуса приближенной теории, годной при низких энергиях. Ярлык «низких энергий» был просто убийственным, несмотря даже на то, что в данном контексте низкоэнергетическими считались частицы, в миллиард миллиардов раз превосходящие по энергии те, что образуются при взрыве тротила. Будь супергравитация низкоэнергетическим приближением, ее нельзя было бы считать фундаментальной теорией Вселенной. Вместо нее на эту роль претендовали целых пять различных теорий суперструн. Но какая же именно из этих пяти струнных теорий описывает нашу Вселенную? И как можно построить теорию струн за пределами того приближения, в котором струны представляются поверхностями с одним пространственным и одним временным измерением в плоском пространстве-времени? Не могут ли струны искривлять фон пространства-времени?
В следующие за 1985-м годы постепенно становилось ясно, что теория струн не дает законченной картины. Начать с того, что струны, как выяснилось, лишь один из элементов широкого класса объектов, которые могут иметь более одного измерения. Пол Таунсенд, который является, как и я, сотрудником факультета прикладной математики и теоретической физики Кембриджа и по большей части заложил основу для изучения таких объектов, стал называть их «р-бранами». Такая р-брана имеет протяженность в р направлениях. Так, при р = 1 брана является струной, при р = 2 — поверхностью или мембраной и т. д. (рис. 2.15).
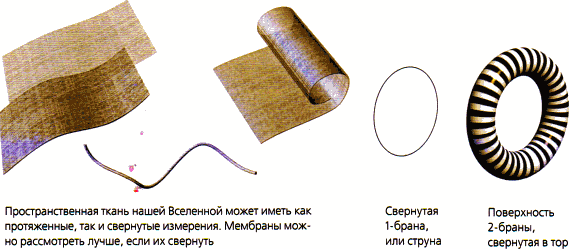
Рис. 2.15. Р-браны
Р-браны — это объекты, протяженные в р измерениях. Частными их случаями являются струны, для которых р = 1, и мембраны (р = 2), но в 10- или 11-мерном пространстве-времени возможны и большие значения р. Часто некоторые или все из р измерений свернуты наподобие тора.

По-видимому, нет причин отдавать предпочтение струнам с р = 1 перед струнами с другими значениями р. Напротив, следует принять принцип р-бранной демократии: все р-браны созданы равными.

Все р-браны можно найти как решения уравнений теории супергравитации в 10 или 11 измерениях. Хотя 10 или 11 измерений, кажется, не слишком похожи на знакомое нам пространство-время, идея состоит в том, что дополнительные 6 или 7 измерений свернуты до такой малой величины, что мы их не замечаем; нам видны только остальные 4 больших и почти плоских измерения.
Должен сказать, что я с неохотой принимаю идею дополнительных измерений. Но для меня, как для позитивиста, вопрос «Существуют ли дополнительные измерения на самом деле?» не имеет смысла. Все, о чем можно спросить: действительно ли математическая модель с дополнительными измерениями хорошо описывает Вселенную? У нас пока нет наблюдений, объяснение которых требовало бы дополнительных измерений. Однако есть вероятность, что они могут появиться на Большом адронном коллайдере LHC в Женеве. Но вот что заставляет многих людей, включая меня, всерьез принимать модели с дополнительными измерениями: это наличие между этими моделями целой сети неожиданных соотношений, называемых дуальностями. Данные соотношения показывают, что все модели, по сути, являются эквивалентными, они лишь отражают разные аспекты одной и той же лежащей в основе теории, которую назвали М-теорией. Не воспринимать эту сеть дуальностей как знак того, что мы находимся на верном пути, было бы все равно что верить, будто Бог поместил среди камней ископаемые остатки, чтобы запутать Дарвина в вопросе об эволюции жизни.
Дуальности показывают, что все пять теорий суперструн описывают одну и ту же физическую реальность и что они к тому же эквивалентны супергравитации (рис. 2.16).
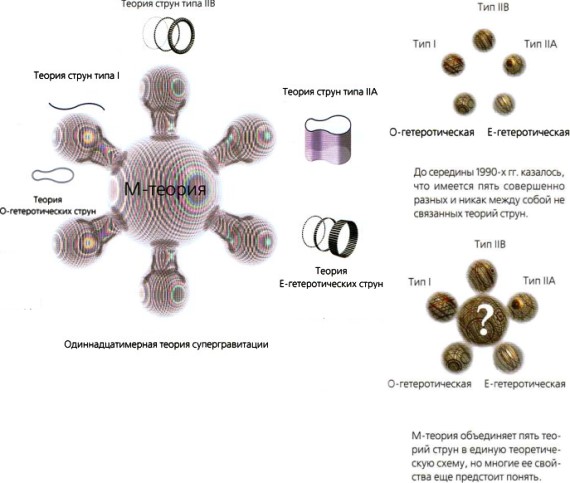
Рис. 2.16
Существует сеть взаимосвязей, так называемых дуальностей, которые соединяют все пять теорий струн, а также 11-мерную супергравитацию. Дуальности предполагают, что разные теории струн — это лишь разные выражения одной и той же фундаментальной концепции, которую называют М-теорией.
Нельзя говорить, что суперструны фундаментальнее супергравитации, и наоборот. Скорее, они являются разными представлениями одной и той же фундаментальной теории, и каждый подход удобен для работы со своим классом задач. Поскольку теории струн не содержат бесконечностей, они хорошо подходят для расчета того, что случается, когда несколько высокоэнергетических частиц сталкиваются и рассеиваются друг на друге. Однако они не слишком полезны для описания того, как энергия очень большого числа частиц искривляет Вселенную или образует связанное состояние, подобное черной дыре. В таких ситуациях требуется супергравитация, которая в основе представляет собой эйнштейновскую теорию искривленного пространства с некоторыми дополнительными типами материи. Именно эту картину я буду в основном использовать в дальнейшем.
Чтобы описать, как квантовая теория придает форму времени и пространству, будет полезно ввести концепцию мнимого времени. Термин «мнимое время» звучит так, будто заимствован из научной фантастики, но это вполне определенная математическая концепция: время, измеряемое так называемыми мнимыми числами. Можно представлять себе обычные действительные числа, такие как 1, 2, -3,5 и т. п., как соответствующие точки на оси, прочерченной слева направо: ноль в середине, положительные действительные числа — справа, отрицательные — слева (рис. 2.17).
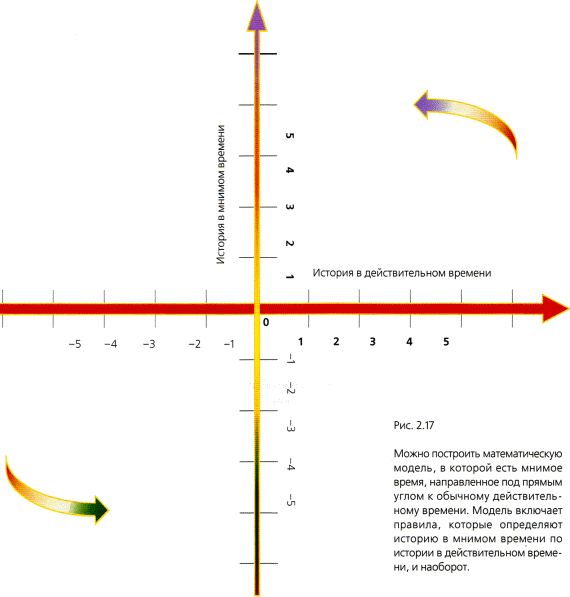
Мнимые числа правомерно изобразить соответствующими отсчетами на вертикальной оси: ноль опять посередине, положительные мнимые числа — вверху, отрицательные мнимые — внизу. То есть мнимые числа допустимо представлять себе как новый тип чисел, расположеных под прямым углом к вещественным числам. Поскольку это чисто математическая конструкция, они не нуждаются в физической реализации; никто, например, не может иметь мнимое число органов или мнимый счет по кредитной карте (рис. 2.18).
Рис 2.18
Мнимые числа — это математическая конструкция. У вас не может быть мнимого счета по кредитной карте.
Можно подумать, будто мнимые числа — это просто математическая игра, не имеющая никакого отношения к реальному миру. С точки зрения позитивистской философии, однако, невозможно определить, что является реальным. Все, что можно сделать, — это находить математические модели, описывающие Вселенную, в которой мы живем. Оказывается, математические модели, использующие мнимое время, предсказывают не только эффекты, которые мы уже наблюдаем, но также эффекты, которые мы пока не можем измерить, но в которые верим по другим причинам. Так что же все-таки действительно, а что мнимо? Неужели вся разница лишь в нашем сознании?
Классическая (то есть неквантовая) общая теория относительности Эйнштейна объединяет действительное время и три измерения пространства в четырехмерное пространство-время. Но направление действительного времени отличается от трех пространственных измерений: мировая линия, или история наблюдателя, всегда направлена в сторону возрастания действительного времени (это означает, что время всегда течет из прошлого в будущее), но она может пролегать как в направлении увеличения, так и в сторону уменьшения любого из трех пространственных измерений. Иными словами, можно развернуться в обратную сторону в пространстве, но не во времени (рис. 2.19).
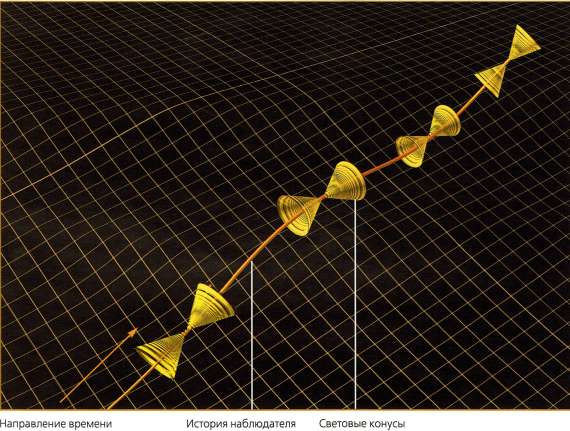
Рис. 2.19
В классическом пространстве-времени общей теории относительности действительное время отличается от пространственных направлений тем, что в направлении истории наблюдателя оно только увеличивается, тогда как пространственные координаты могут как увеличиваться, так и уменьшаться по ходу этой истории. С другой стороны, мнимое время квантовой теории подобно дополнительному пространственному измерению, поскольку может как увеличиваться, таки уменьшаться.
С другой стороны, поскольку мнимое время расположено под прямым углом к действительному, оно ведет себя подобно четвертому пространственному измерению. Поэтому оно может обладать гораздо более широким диапазоном возможностей, чем железнодорожная колея обычного действительного времени, которое может лишь иметь начало или конец либо замыкаться в круг. Именно в этом «мнимом» смысле время имеет форму.
Чтобы увидеть подобные возможности, представим пространство-время с мнимым временем как сферу, подобную поверхности Земли. Предположим, что мнимое время соответствует широте (рис. 2.20). Тогда история Вселенной в мнимом времени начинается на южном полюсе. Не имеет смысла вопрос «Что случилось до начала?». Таких моментов времени просто нет, точно так же, как точек южнее южного полюса. Полюс — самая обыкновенная точка на поверхности Земли, и там работают те же самые законы, что и в других точках. Это наводит на мысль, что начало Вселенной в мнимом времени может быть обычной точкой пространства-времени и что в начале должны соблюдаться все законы, которые действуют в остальной Вселенной. (Квантовое происхождение и эволюция Вселенной будут обсуждаться в следующей главе.)
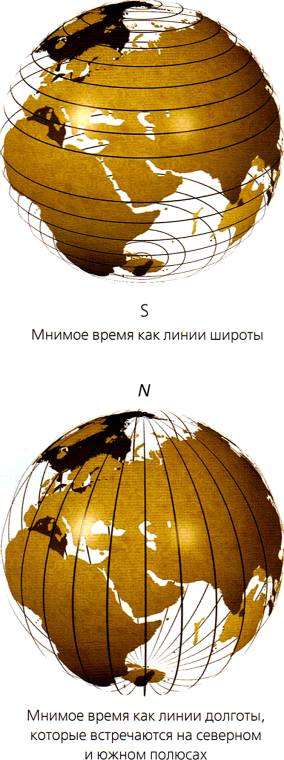
Рис. 2.20 и 2.21. Мнимое время
Рис. 2.20: В мнимом пространстве-времени, которое является сферой, направление мнимого времени может быть представлено расстоянием от южного полюса. При движении на север круги долготы, проходящие на постоянном расстоянии от южного полюса, становятся все больше и больше, что соответствует расширению Вселенной в мнимом времени. У экватора Вселенная достигает максимального размера и затем с увеличением мнимого времени вновь сжимается в точку на северном полюсе. Но хотя размер Вселенной становится на полюсах нулевым, в этих точках не будет сингулярностей просто потому, что Северный и Южный полюсы — совершенно обыкновенные точки на земной поверхности. Это указывает на то, что в мнимом времени рождение Вселенной может быть обычной точкой пространства-времени.
Рис. 2.21: Вместо широты направлению мнимого времени в сферическом пространстве-времени может соответствовать долгота. Поскольку все линии постоянной долготы сходятся в северном и южном полюсах, время там останавливается; увеличение мнимого времени оставляет вас на одном и том же месте, подобно тому как движение на запад на Северном полюсе Земли оставляет вас на Северном полюсе.
Другой вариант поведения можно проиллюстрировать, если считать мнимое время долготой на Земле. Все меридианы сходятся на северном и южном полюсах (рис. 2.21). Так что время здесь останавливается в том смысле, что увеличение мнимого времени (или градуса долготы) оставляет вас на одном и том же месте. Это очень похоже на то, как обычное время кажется остановившимся на горизонте черной дыры. Мы выяснили, что это замирание действительного или мнимого времени (как обоих сразу, так и по одному) означает, что пространство-время имеет температуру, как это было открыто мною для случая черных дыр. Но черные дыры имеют не только температуру, они к тому же ведут себя так, будто обладают энтропией. Энтропия — это мера числа внутренних состояний (различных вариантов внутренней конфигурации), которые может иметь черная дара, не меняя своего вида для внешнего наблюдателя, способного определить только ее массу, вращение и электрический заряд. Энтропия черной дыры выражается очень простой формулой, которую я вывел в 1974 г. Она равна площади горизонта черной дыры: один бит информации о ее внутреннем состоянии приходится на каждую фундаментальную единицу площади горизонта.
Формула для энтропии черной дыры
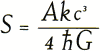
A площадь горизонта событий черной дыры
ħ постоянная Планка
k постоянная Больцмана
G гравитационная постоянная Ньютона
c скорость света
S энтропия
Это говорит о глубокой связи между квантовой гравитацией и термодинамикой — наукой о теплоте (к сфере которой относится понятие энтропии).
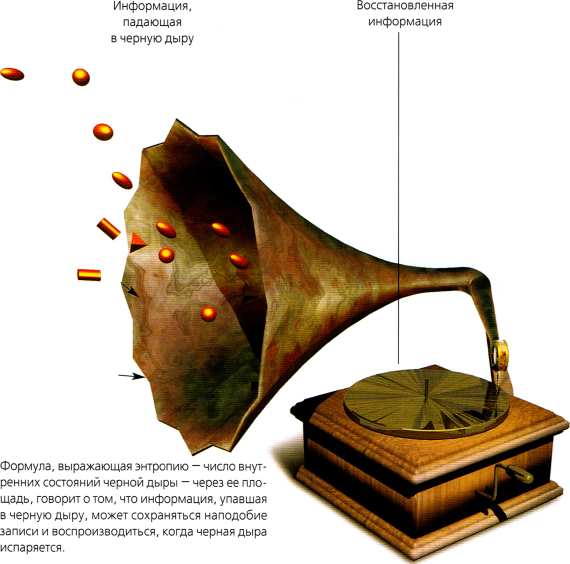
А еще наводит на мысль, что квантовая гравитация может проявлять своего рода голографические свойства (рис. 2.22).
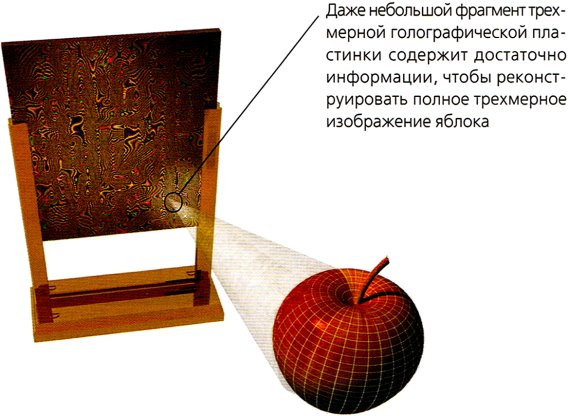

Рис. 2.22.
По сути, голография — это проявление интерференции волн. Голограмма создается, когда свет от одного лазера разделяется на два отдельных пучка а и b. Один из них (b) рассеивается объектом сна светочувствительную пластинку d. Другой (а) проходит через линзу е и взаимодействует с рассеянным светом пучка b, создавая на пластинке интерференционный узор. Когда лазер светит сквозь проявленную пластинку, восстанавливается полное трехмерное изображение исходного объекта. Наблюдатель может обойти голографическое изображение и увидеть скрытые поверхности, которые на обычной фотографии не видны.
Двумерная поверхность пластинки (слева), в отличие от обычной фотографии, обладает замечательным свойством: любой, даже небольшой, фрагмент ее поверхности содержит всю информацию, необходимую для реконструкции целого изображения.
Голографический принцип
Осознание того, что площадь поверхности горизонта, окружающего черную дыру, является мерой ее энтропии, навело на мысль о том, что максимальная энтропия любой замкнутой области никогда не может превзойти четверть площади охватывающей поверхности. Поскольку энтропия не что иное, как мера полной информации, содержащейся в системе, информация, связанная со всеми явлениями в трехмерном мире, может быть сохранена на его двумерной границе, подобно голографическому изображению. В определенном смысле мир можно было бы считать двумерным.
Информация о квантовых состояниях внутри области пространства-времени может быть неким образом закодирована на ее границе, которая имеет на два измерения меньше. Это похоже на то, как голограмма содержит трехмерное изображение на двумерной поверхности. Если квантовая гравитация включает голографический принцип, это может означать, что у нас есть шанс проследить, что происходит внутри черной дыры. Большое значение имеет возможность предсказывать излучение, исходящее из черной дыры. Если это невозможно, значит, нельзя и предсказывать будущее настолько точно, как мы думаем. (Данный вопрос обсуждается в главе 4. Голографии посвящена глава 7.) Похоже, мы сами можем жить на 3-бране — четырехмерной (три пространственных плюс одно временное измерение) поверхности, которая ограничивает пятимерную область, а остальные размерности свернуты до очень малых размеров. При этом в состоянии мира на бране зашифровано то, что происходит в пятимерной области.

