Книга: Истина и красота. Всемирная история симметрии.

Дальше: Глава 15 Математическая кутерьма

Глава 14
Политический журналист

В июне 1972 года во время кампании по выборам президента США охранник в Уотергейтском комплексе заметил на одной из дверей скотч и оборвал его, решив, что, должно быть, его случайно оставили рабочие. Однако, когда он вернулся, скотч снова оказался на месте — им был заклеен язычок замка. Это вызвало подозрение, охранник позвонил в полицию, и та арестовала пятерых человек, проникших в помещение Национального комитета Демократической партии. Оказалось, они связаны со штабом по переизбранию президента Никсона.

Это событие не оказало большого влияния на сами выборы — Никсон победил с внушительным перевесом. Но историю не удалось замять, и щупальца Уотергейтского дела начали постепенно проникать все глубже и глубже в администрацию Никсона.

Два репортера из Washington Post, Боб Вудворд и Карл Бернстайн, вцепились в это дело бульдожьей хваткой. Журналисты получали секретную информацию от осведомителя, известного под псевдонимом Глубокая Глотка. Никто не знал, кто этот человек, однако все понимали, что это лицо занимает очень высокий административный пост. В 2005 году выяснилось, что Глубокой Глоткой был Марк Фелт, второй человек в Федеральном бюро расследований.

Информация, благодаря ему просочившаяся в прессу, имела эффект разорвавшейся бомбы. К апрелю 1974 года Никсону пришлось отправить в отставку двух своих высокопоставленных помощников. Как выяснилось, президент установил «жучки» в собственном кабинете, и имелись пленки с записью довольно деликатных разговоров. После юридического сражения за доступ к пленкам в некоторых записях обнаружились пробелы, по всей вероятности — результат целенаправленного стирания.

Попытка скрыть то обстоятельство, что между проникновением со взломом и Белым Домом существует непосредственная связь, воспринималась практически всеми как преступление худшее, чем сам взлом. Палата Представителей начала формальный процесс, который мог привести к импичменту президента по обвинению в «тяжких преступлениях и правонарушениях» перед Сенатом США; в случае установления вины ему грозила отставка. Когда импичмент и осуждение стали неотвратимы, Никсон сам подал в отставку.

Противником Никсона на выборах был сенатор Джордж Макговерн. Объявляя в Сью Фоллс, штат Южная Дакота, о выдвижении своей кандидатуры от Демократической партии, Макговерн сделал несколько пророческих замечаний: «Сегодня наши граждане более не чувствуют, что они могут строить собственную жизнь во взаимодействии со своими согражданами. Происходит это из-за потери доверия к правдивости и здравому смыслу наших лидеров. Самым тягостным новым оборотом в американском политическом словаре стало выражение „кризис доверия“, который проявляется в разрыве между риторикой и реальностью. Говоря откровенно, это означает, что люди больше не верят в то, что говорят им их лидеры».

Среди второстепенных фигур в кампании Макговерна был начинающий политический журналист, карьера которого, вероятно, пошла бы вверх, одержи Макговерн победу на выборах. В том варианте истории политика могла бы обогатиться, но фундаментальная физика и продвинутая математика стали бы намного беднее. В 2004 году — в той истории, которая на самом деле осуществилась — этот журналист фигурировал в списке журнала Time среди сотни самых влиятельных людей за год, но попал он туда не в связи с журналистикой.

Он оказался в списке за свои новаторские вклады в математическую физику. На его счету некоторые из наиболее оригинальных математических построений в мире, за которые он получил Филдсовскую медаль — высшую награду в математике, сравнимую по престижности с Нобелевской премией. Однако он не математик. Он — один из ведущих в мире физиков-теоретиков и награжден Национальной научной медалью, хотя по своему первому образованию он историк. А кроме того, он — один из главных пропагандистов (хотя и не совсем оригинальный творец) самых передовых современных усилий по объединению всей физики. Он занимает должность профессора математической физики в Институте высших исследований в Принстоне, где некогда работал Эйнштейн, а зовут его Эдвард Виттен.

Подобно немецким отцам квантовой теории и в отличие от несчастного Дирака, Виттен вырос в интеллектуальной среде. Его отец Луи Виттен — тоже физик, работающий в области общей теории относительности и гравитации. Эдвард родился в Балтиморе, штат Мэриленд, и начал обучение в университете Брандайс. После переизбрания Никсона он вернулся к академической жизни, защитив диссертацию в Принстонском университете, и стал работать и преподавать в различных американских университетах. В 1987 году его приняли в Институт высших исследований, где все академические должности — чисто исследовательские; там он работает и поныне.

Виттен начал исследования в квантовой теории поля — в области, представляющей собой первые плоды усилий по согласованию квантовой теории с теорией относительности. Релятивистские эффекты движения там учитываются, но только в плоском пространстве-времени. (А гравитация, которая требует искривленного пространства-времени, не рассматривается.) В 1998 году в своей гиббсовской лекции Виттен сказал, что квантовая теория поля «охватывает большую часть того, что нам известно о законах физики, за исключением гравитации. Семидесятилетняя история ее развития включает в себя много значимых вех — от теории „антиматерии“ до более точного описания атомов и Стандартной Модели физики частиц». Он отметил, что, развитая в большей своей части физиками, квантовая теория поля в значительной степени лишена математической строгости и поэтому не оказала большого влияния на математику как таковую.

Подошло время, продолжал Виттен, исправить этот дефект. Несколько важных областей чистой математики, по сути дела, являются квантовой теорией поля, но в иных одеждах. Собственный вклад Виттена — открытие и анализ топологических квантовых теорий поля — допускал прямую интерпретацию в терминах концепций, изобретенных целым рядом чистых математиков в рамках весьма различных контекстов. Сюда относится эпическое открытие, сделанное английским математиком Саймоном Доналдсоном, что четырехмерные пространства уникальны в том отношении, что допускают существование многих различных «дифференцируемых структур» — систем координат, в которых можно строить дифференциальное исчисление. Среди других аспектов — недавнее крупное открытие в теории узлов, известное как многочлены Джонса, явление, называемое зеркальной симметрией в теории многомерных комплексных поверхностей, и несколько областей из современной теории алгебр Ли.

Виттен сделал смелое предсказание — одной из важнейших тем в математике двадцать первого века будет интегрирование в основное течение математики идей из квантовой теории поля: «Перед нами здесь раскинулся обширный горный хребет, большая часть которого все еще скрыта в тумане. В математических теориях сегодняшнего дня видны только самые высокие вершины, возвышающиеся над облаками, и эти восхитительные вершины исследуются в отрыве друг от друга. В дымке все еще скрыт сам хребет, покоящийся на гранитном основании квантовой теории поля, а вместе с ним скрыты и россыпи математических сокровищ».

Филдсовская медаль была присуждена Виттену за открытие нескольких из этих скрытых сокровищ. Среди них — новое улучшенное доказательство «гипотезы о положительности массы», в силу которой гравитационная система с положительной локальной плотностью массы должна иметь положительную полную массу. Это может показаться очевидным, но в квантовом мире масса — тонкая материя. Доказательство этого результата, долго стоявшего на повестке дня, было опубликовано Ричардом Шеном и Шинтаном Яу в 1979 году и принесло Яу Филдсовскую медаль за 1982 год. В новом улучшенном доказательстве Виттена использовалась суперсимметрия. То было первое применение этой концепции к важной математической проблеме.

Суперсимметрию можно понять в терминах старой головоломки, в которой спрашивается, какая пробка подойдет к бутылке, отверстие в которой может быть круглым, квадратным или треугольным. Удивительно, но требуемая форма существует, и стандартный ответ — пробка с круглым основанием, которая сходится к острию как клин. При взгляде снизу она видится окружностью; спереди — квадратом; сбоку — треугольником. Одна форма способна выполнить все три задачи, потому что трехмерный объект может иметь несколько различных «теней», или проекций, в различных направлениях.

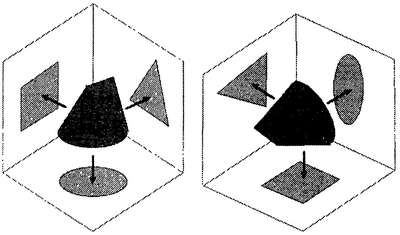
Как работает суперсимметрия. Слева: пробка, подходящая к отверстиям трех разных форм. Справа: эффект вращения пробки.

Теперь представим себе флатландца, живущего на «полу» моего рисунка, так что ему видна проекция пробки на пол, но он и не подозревает о других проекциях. В один прекрасный день он, к своему изумлению, обнаруживает, что круглая форма каким-то образом изменилась и стала квадратом. Как такое может быть? Это определенно не симметрия.

Не симметрия — да, во Флатландии. Но когда флатландец отвернулся, кто-то, живущий в трехмерии, повернул пробку так, что ее проекция на пол превратилась в квадрат. При этом в трехмерии вращение является преобразованием симметрии. Так что симметрия в более высокой размерности может иногда объяснить совершенно непостижимое преобразование в более низкой размерности.

Нечто очень похожее происходит в суперсимметрии, но вместо превращения окружности в квадрат фермионы там превращаются в бозоны. Это удивительно. В самом деле, вы можете выполнить вычисления с фермионами, напустить на каждый операцию суперсимметрии и получить результат для бозонов без всяких дополнительных усилий. Или наоборот.

Подобного мы ожидаем от настоящих симметрий. Если вы стоите перед зеркалом и жонглируете мячиками, то все происходящее с вашей стороны зеркала полностью определяет происходящее с другой стороны. Ваш образ там жонглирует образами мячиков. Если выполнение последовательности приемов занимает 3,79 с с этой стороны зеркала, то без всяких измерений ясно, что выполнение той же последовательности приемов займет 3,79 с с другой стороны. Две ситуации связаны зеркальной симметрией; что бы ни происходило с одной стороны, оно происходит также и в отражении.

Суперсимметрии не настолько просты, но приводят к похожему эффекту. Они позволяют вывести свойства частиц одного типа из свойств частиц совершенно иного типа. Дело обстоит почти так же, как если бы вы могли забраться куда-то в высокомерную область вселенной и там повернуть фермион, превратив его в бозон. Частицы организуются в суперсимметричные пары: обычной частице отвечает ее повернутая версия, называемая счастицей. Электроны имеют в паре с собой сэлектроны, кварки — скварки. По историческим причинам близнец фотона называется не сфотон, а фотино. Имеется своеобразный «теневой мир» счастиц, который только слабо взаимодействует с обычным миром.

В ногу с этой идеей идет изящная математика, но массы этих предсказываемых теневых частиц слишком велики для того, чтобы их можно было наблюдать в экспериментах. Суперсимметрия прекрасна, но может не быть истинной. Но даже если вопрос не состоит в прямом подтверждении, вполне возможными могут оказаться подтверждения косвенные. Наука проверяет теории главным образом через их следствия.

Виттен активно развивал суперсимметрию и в 1984 году написал статью, озаглавленную «Суперсимметрия и теория Морса». Теория Морса — это область топологии, названная по имени своего первоисследователя Марстона Морса, в которой устанавливается связь общей формы некоторого пространства с его пиками и долинами. Сэр Майкл Атья — вероятно, наиболее крупный из ныне здравствующих британских математиков — считает, что статья Виттена представляет собой «обязательное чтение для геометров, заинтересованных в понимании современной квантовой теории поля. Она также содержит блестящее доказательство классического неравенства Морса. Реальная цель статьи состоит в подготовке почвы для суперсимметричной квантовой теории поля в терминах бесконечномерных многообразий». В дальнейшем Виттен применил эти методы к другим актуальным вопросам на дальних рубежах топологии и алгебраической геометрии.

Должно быть понятно, что, когда я сказал, что Виттен не математик, я не имел в виду отсутствие у него математического таланта. Как раз наоборот — быть может, ни у кого на планете нет большего математического таланта. Но в случае Виттена к этому добавляется удивительная физическая интуиция.

В отличие от математиков физики редко стесняются использовать физическую интуицию, чтобы перескочить через пробел в математической логике. Математики же привыкли относиться к «мостам веры» с подозрением вне зависимости от того, сколь много имеется подтверждающих свидетельств: для математиков доказательство — это все. Виттен необычен в том отношении, что он может соотносить свою интуицию с той математикой, которая понятна математикам. Атья выражает это такими словами: «Его способность интерпретировать физические идеи в математических терминах совершенно уникальна. Снова и снова он удивляет математическое сообщество своими блестящими физическими озарениями, приводящими к новым глубоким математическим теоремам».

Но у этой интуитивной мощи есть и оборотная сторона. Многие из важнейших Виттеновых идей, выведенных из физических принципов или аналогий, появились без доказательств, а в отношении некоторых доказательства отсутствуют и по сей день. Не в том дело, что он не может дать доказательства, — может, как показывает его Филдсовская медаль, — а в том, что он может делать логические скачки, ведущие к глубокой и верной математике, словно бы не нуждаясь в доказательствах.

Главный вопрос — имеет ли изящная виттеновская математика какое-нибудь отношение к фундаментальной физике? Или же поиски красоты завели в математический тупик, где потеряна всякая связь с физической истиной? К 80-м годам двадцатого века физики объединили три из четырех взаимодействий, имеющихся в природе: электромагнитное, слабое и сильное. Но Теории Великого Объединения ничего не говорят о гравитации. Сила, которую мы наиболее непосредственно ощущаем в повседневной жизни, которая буквально не дает нам витать в облаках, исключена из синтеза — конфуз?

Достаточно несложно написать комбинированную теорию, включающую гравитацию и квантовую теорию и с виду выглядящую разумно. Но при всякой попытке решить получающиеся там уравнения возникает бессмыслица. Как правило, числа, призванные выражать разумные физические величины, оказываются бесконечными. Бесконечность в физической теории указывает: что-то идет не так. Именно появление бесконечности в законе излучения подтолкнуло Планка к квантованию света.

Некоторые физики пришли к убеждению, что основной источник бесконечностей — это укоренившаяся привычка рассматривать частицы как точечные. Точка — местоположение без размера — представляет собой математическую фикцию. Квантовые частицы — вероятностным образом размазанные точки, но это не приносит полного облегчения; требуются какие-то более сильные средства. Даже в 70-х годах двадцатого века несколько первооткрывателей начали думать, что частицы можно разумным образом смоделировать как колебания очень маленьких петель — «струн». В 80-х, когда в дело вступила суперсимметрия, эти струны превратились в суперструны.

О суперструнах можно написать целую книгу, и таких книг в самом деле существует уже несколько, но мы обойдемся очень приближенным описанием, получаемым в основном путем размахивания руками. Я хочу выделить четыре свойства: способ, которым объединяются релятивистская и квантовая картины, нужда в дополнительных измерениях, интерпретация квантовых состояний как колебаний в этих дополнительных измерениях и симметрии дополнительных измерений — или, точнее, различных полей, которые в них живут.

Начнем с эйнштейновской идеи представления траектории частицы в пространстве-времени в виде кривой, которую он назвал мировой линией данной частицы. По существу, это кривая, которую частица описывает в пространстве-времени по мере своего движения. В теории относительности мировые линии — гладкие кривые, что определяется видом полевых уравнений Эйнштейна. Они не ветвятся, потому что в теории относительности будущее любой системы полностью определяется ее прошлым, даже ее настоящим.

Имеется аналогичная концепция в квантовой теории поля, называемая фейнмановскими диаграммами. Фейнмановские диаграммы описывают взаимодействие частиц в весьма схематичном пространстве-времени. Например, на рисунке слева показана фейнмановская диаграмма для электрона, испускающего фотон, который затем улавливается другим электроном. По традиции фотоны обозначаются волнистыми линиями.

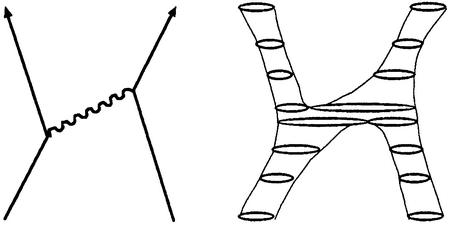
Слева: фейнмановская диаграмма для взаимодействующих частиц. Справа: соответствующие мировые листы, в сечениях которых показаны струны.

Фейнмановская диаграмма несколько напоминает релятивистскую мировую линию, но у нее острые углы и она ветвится. В 70-х годах XX века в голову Йоиширо Намбу пришла мысль, что если вместо гипотезы о том, что частицы точечные, принять, что они представляют собой маленькие петли, то фейнмановские диаграммы можно превратить в гладкие поверхности — мировые листы, как показано на правой картинке. Мировой лист можно интерпретировать как мировую линию в модифицированном пространстве-времени с дополнительными размерностями, в которых живут петли.

Что здорово насчет петель — помимо того что они не точки, — так это их способность колебаться. Быть может, каждая мода колебаний соответствует квантовому состоянию. Это позволит объяснить, почему квантовые состояния всегда содержат целые кратные некоторой базисной величины — например, спина, который всегда есть целое кратное √¹/₂. Число волн, помещающихся на петле, должно быть целым числом. На скрипичной струне эти различные моды колебаний являются основным тоном и его высшими гармониками. Так что квантовая теория становится определенного вида музыкой, исполняемой на суперструнах вместо скрипичных струн.

Идея Намбу не взялась из ниоткуда. Она уходит своими корнями в замечательную формулу, выведенную Габриэле Венециано в 1968 году, которая показывала, что по видимости различные фейнмановские диаграммы представляют один и тот же физический процесс и что стоит только обойти этот факт вниманием, как вычисления в квантовой теории поля приведут к неправильному ответу. Намбу заметил, что, когда фейнмановские диаграммы окружаются трубками, различные диаграммы приводят к системе трубок с одной и той же топологией. Другими словами, системы трубок можно деформировать друг в друга. Так формула Венециано оказалась связана с топологическими свойствами трубок.

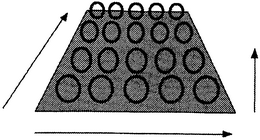
Струны выталкиваются из обычного пространства-времени в новое измерение.

Это в свою очередь подсказывало, что квантовые частицы, несущие свои дискретные квантовые числа типа заряда, могут быть топологическими свойствами гладкого пространства-времени. Математики уже были свидетелями того, как основные топологические свойства — такие как число дыр на поверхности — имеют тенденцию к дискретности. Вроде все сходилось. Но дьявол, как всегда, сидит в деталях, а детали оказались дьявольскими. Теория струн была первой попыткой получить детали, пребывающие в согласии с реальным миром.

Теория струн возникла вовсе не как способ построить Теорию Всего, а как некоторое предложение, высказанное для объяснения частиц, известных под собирательным названием адронов. Эти частицы включают в себя большую часть обычных частиц, обнаруживаемых в атомных ядрах, таких как протон и нейтрон, а также толпу более экзотических частиц. Однако в теории есть изъян: она предсказывает существование частицы с нулевой массой и спином 2, которая до тех пор (как и поныне) не наблюдалась. Кроме того, она не смогла предсказать ни одной частицы со спином ¹/₂, в то время как многие адроны, включая протон и нейтрон, имеют спин ¹/₂. Это похоже на летний прогноз погоды, который предсказывает градины в полметра диаметром, но ничего не говорит о том, будет ли тепло. Физики не впечатлились. В 1974 году, когда на арене появилась квантовая хромодинамика и не только объяснила все известные адроны, но даже успешно предсказала новый (омега-минус), судьба теории струн представлялась решенной.

В тот момент, однако, Джон Шварц и Жоэль Шерк заметили, что нежеланная частица с нулевой массой и спином 2, возникающая в теории струн, могла бы оказаться давно искомым гравитоном — гипотетической частицей, которая, согласно современным представлениям, должна переносить гравитационную силу. Могла ли теория струн оказаться квантовой теорией не адронов, а гравитации? Если да, то она стала бы привлекательным соперником Теории Всего — ладно, Теории Много Чего, потому что есть много частиц, не являющихся адронами.

В тот момент в игру вступила суперсимметрия, потому что именно она превращает фермионы в бозоны. Адроны включают в себя частицы обоих сортов, хотя ряд других частиц, например электрон, не являются адронами. Если суперсимметрию можно было бы включить в теорию струн, то в теоретической модели автоматически появился бы целый ряд новых частиц, возникающих как суперсимметричные партнеры тех частиц, что уже присутствовали в модели.

Комбинированная теория, созданная Пьером Рамоном, Андрэ Неве и Шварцем, была теорией суперструн. Она включала частицы со спином −2, и в ней не было неприятного свойства обычной теории струн — появления частиц, движущихся быстрее света. Присутствие таких частиц в теории теперь рассматривается как свидетельство неустойчивости, из-за чего такие теории следует исключить из рассмотрения.

Начиная с 1980 года британский физик-теоретик Майкл Грин постепенно разрабатывал математику суперструн, используя методы теории групп Ли и топологии, и вскоре стало ясно, что, независимо от имеющихся у нее верительных грамот со стороны физики, теория суперструн обладает необычайной математической красотой. Физики продолжали упорствовать: в 1983 году Луис Алварес-Гомэ и Виттен обнаружили новую загвоздку с теориями струн, включая и суперструны, а заодно и с доброй старой квантовой теорией поля. А именно — эти теории, как правило, обладали аномалиями. Аномалия возникает, когда процесс превращения классической системы в ее квантовый аналог изменяет важные симметрии.

Еще раньше Грин и Шварц открыли, что в очень специальных случаях аномалии волшебным образом исчезают, но только если пространство-время имеет размерность 26 (в первом варианте теории, называемом бозонной теорией струн) или 10 (в позднейших модификациях). Почему? В вычислениях, относящихся к бозонной теории струн, математические слагаемые, которые могли бы создать аномалию, умножаются на d − 26, где d — размерность пространства-времени. Так что эти члены обращаются в нуль в точности когда d = 26. Аналогичным образом, в модифицированном варианте соответствующий множитель оказывается равным d − 10. Время всегда остается одномерным, но пространство требует дополнительных 6 или 22 измерений. Шварц выразил это так:

В 1984 году мы с Майклом Грином занимались вычислениями в одной из этих теорий суперструн с целью выяснить, действительно ли там появляется аномалия. То, что мы открыли, было удивительно. Мы нашли, что, вообще говоря, действительно имеется аномалия, делавшая теорию неудовлетворительной. Но имелась свобода в выборе конкретной симметрии, используемой уже в момент определения теории. На самом деле имелось бесконечно много возможностей выбора этих симметрий. Однако всего для одной из них аномалия магически сокращалась в формулах, тогда как для всех остальных не сокращалась. Таким образом, среди этой бесконечности возможностей оказалась выделенной одна-единственная, которая была потенциально непротиворечивой.

Если бы можно было не обращать внимания на неудобоваримые числа 10 и 26, это было бы восхитительное открытие. Оно подсказывало, что может иметься математическая причина, в силу которой пространство-время обладает вполне определенным числом измерений. Разочаровывал только тот факт, что число это — не четыре. Но то было только начало! Физики всегда задавались вопросом, почему пространство-время имеет ту размерность, которую мы видим; теперь же дело выглядело так, будто на этот вопрос можно найти ответ получше, чем «ну да, вообще-то размерность может быть любой, но в нашей вселенной она как раз равна четырем».

Возможно, другие теории могли бы привести к четырехмерному пространству-времени. Такая ситуация была бы идеальна, однако ничего в этом духе не сработало — необычные размерности отказывались убираться с дороги. Так что, может быть, они появляются по делу? В этом состояла старая идея Калуцы: пространство-время может иметь дополнительные размерности, которые мы просто не в состоянии наблюдать. Если так, то струны могли бы оставаться одномерными петлями, но такими, которые колеблются в более высокомерных пространствах, никаким иным способом не видимых. Квантовые числа, связанные с частицами, такие как заряд или очарование, могли бы определяться видом таких колебаний.

Фундаментальный вопрос состоял в том, как выглядят скрытые размерности. Какую форму имеет пространство-время?

Сначала физики надеялись, что дополнительные размерности образуют нечто простое, например, 6-мерный аналог тора. Но в 1985 году Филипп Канделас, Гари Хоровиц, Эндрю Строминджер и Виттен привели аргументы, показывающие, что самая подходящая форма дается так называемыми многообразиями Калаби-Яу. Имеются десятки тысяч таких геометрических форм; на рисунке схематично изображено типичное многообразие Калаби-Яу.

(Иллюстрация предоставлена Эндрю Дж. Хансоном, профессором университета Индианы)

Огромное преимущество многообразий Калаби-Яу состоит в том, что суперсимметрия 10-мерного пространства-времени наследуется получающимся из него обыкновенным четырехмерным пространством-временем.

Впервые исключительные группы Ли начали приобретать значительную роль на передних рубежах физики, и эта тенденция ускорялась. Около 1990 года представлялось, что имеется пять возможных типов теорий суперструн, причем все с пространством-временем размерности 10. Эти теории называются Тип I, Тип IIA и IIB, а также «гетеротические» типы HO и HE. Возникают интересные калибровочные группы симметрий; например, в теориях Типа I и HO имеется SO(32) — группа вращений в 32-мерном пространстве, а в теории Типа HE исключительная группа Ли возникает в комбинации E₈×E₈ — в двух различных экземплярах, действующих различными способами.

Исключительная группа G₂ также возникла в самом последнем повороте сюжета, который Виттен называет M-теорией. Буква M, по его словам, означает magic, mystery или matrix — «магия, тайна, матрица». В M-теории, основанной на 11-мерном пространстве-времени, объединены все пять 10-мерных теорий струн — в том смысле, что каждую из последних можно получить из M-теории, придавая некоторым ее константам определенные значения. В M-теории многообразия Калаби-Яу заменяются на 7-мерные пространства, известные как G₂-многообразия, из-за того что их симметрии тесно связаны с Киллинговой исключительной группой Ли G₂.

На данный момент заметно некоторое недовольство теорией струн: дело не в том, что она неверна, а в том, что пока не известно, верна ли она. Несколько видных физиков, в особенности экспериментаторов, никогда вообще не связывались с суперструнами — главным образом потому, что те не давали им никакой почвы для работы. Не было новых явлений, доступных наблюдению, не было новых величин, доступных измерению.

Я не склонен считать суперструны ключом ко всей вселенной, но я полагаю, что подобный критицизм не вполне справедлив. От струнных теоретиков требуют доказать свою невиновность, тогда как нормальным образом это критики должны были бы доказывать их вину. Развитие радикально новых способов осмысления физического мира требует долгого времени и значительных усилий, а теория струн технически очень сложна. В принципе она может делать новые предсказания о нашем мире; большая проблема состоит в том, что необходимые вычисления необычайно трудны. Те же претензии можно было 40 лет назад выдвинуть против квантовой теории поля, но в конце концов вычисления там удалось продвинуть вперед за счет совместного применения лучших компьютеров и усовершенствованной математики, и достигнутое согласие с экспериментом оказалось лучше, чем где бы то ни было еще в науке.

Более того, во многом то же самое обвинение можно было бы высказать в адрес почти любого кандидата на роль Теории Всего, причем, парадоксальным образом, чем лучше такая теория, тем труднее будет доказать, что она верная. Причина в самой природе Теории Всего. Чтобы оказаться успешной, она должна согласовываться с квантовой теорией во всех случаях, когда она применяется ко всякому эксперименту, результаты которого согласуются с квантовой теорией. Она должна также согласовываться с теорией относительности во всех случаях, когда она применяется ко всякому эксперименту, результаты которого согласуются с теорией относительности. Так что Теория Всего обязана проходить любую экспериментальную проверку, какую только можно изобрести. Требовать нового предсказания, которое отличает Теорию Всего от стандартной физики, — это все равно что требовать чего-то такого, что приводит к результатам, тождественным тем, которые предсказаны теориями, описывающими все известные физические явления, но при этом от них отличается.

Разумеется, в конце концов теории струн придется сделать новое предсказание и пройти проверку наблюдениями, чтобы из умозрительной стать реальной физической теорией. Необходимость согласования со всем, что на данный момент известно, не исключает возможности таких предсказаний, она просто объясняет, почему они не получаются так запросто. Некоторые предварительные предложения по поводу критических экспериментов уже существуют. Например, недавние наблюдения удаленных галактик показывают, что вселенная не только расширяется, но и делает это с возрастающей скоростью. Теория суперструн предлагает простое объяснение — гравитация утекает в те самые дополнительные измерения. Однако имеются и другие способы объяснить этот конкретный эффект. Во всяком случае не подлежит сомнению, что если все теоретики прекратят исследовать физику суперструн, то мы лишимся возможности узнать, верна ли эта теория. Формулировка и осуществление ключевых экспериментов требуют времени и сил — даже при условии, что такие эксперименты можно провести.

Я не хочу, чтобы у вас сложилось впечатление, будто, когда дело доходит до объединения квантовой теории с теорией относительности, суперструны — единственное, что есть в программе. Имеются и конкурирующие предложения — хотя все они страдают от того же отсутствия экспериментального подтверждения.

Одна идея, известная как некоммутативная геометрия, взращена французским математиком Аленом Конном. Он основывается на новой концепции геометрии пространства-времени. Большинство объединений исходят из идеи, что пространство-время представляет собой некоторое расширение релятивистской модели Эйнштейна, и пытаются как-то подогнать его под существующие фундаментальные частицы субатомной физики. Конн делает наоборот. Он начинает с математической структуры, известной как некоммутативное пространство, которое содержит все группы симметрии, возникающие в Стандартной Модели, а далее выводит свойства, аналогичные относительности. Математика такого пространства восходит к Гамильтону и его некоммутативным кватернионам, однако она сильно обобщена и модифицирована. При этом снова альтернативная теория имеет крепкие связи с теорией групп Ли.

Другая захватывающая идея — петлевая квантовая гравитация. В 80-х годах двадцатого века физик Абэй Аштекар предложил, как выглядели бы уравнения Эйнштейна в квантовой области, где пространство становится «зернистым». Ли Смолин и Карло Равелли развили его идеи, что привело к модели пространства, которое представляет собой нечто вроде средневековой кольчуги, собранной из очень маленьких, сцепленных между собой кусочков порядка 10⁻³⁵ м в поперечнике. Они заметили, что детали структуры кольчуги становятся очень запутанными, когда звенья заузливаются или сплетаются между собой как косы. Однако не ясно, что эти возможности означают.

В 2004 году Санденс Билсон-Томсон открыл, что некоторые из этих кос точно воспроизводят правила сочетаний кварков. Электрический заряд кварка переинтерпретируется здесь в терминах топологии соответствующей косы, а правила их сочетаний следуют из простых геометрических операций с косами. Эта идея, все еще находящаяся во младенчестве, позволяет воспроизвести большинство частиц, наблюдаемых в Стандартной Модели. Она — последняя в ряду гипотетических предложений о том, что материя — реализованная здесь в виде частиц — может оказаться следствием «особенностей» в пространстве, таких как узлы, локализованные волны или более сложные структуры, где пространство перестает быть гладким и регулярным. Если Билсон-Томсон прав, то материя есть лишь скрученное пространство-время.

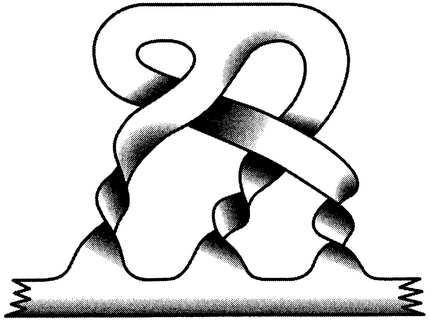
Электрон, представленный в виде косы.

Математики изучали топологию кос в течение многих лет, и давно известно, что косы образуют группу — группу кос. Операция «умножения» в ней состоит в присоединении концов нитей друг к другу — в том же духе, как мы присоединяли друг к другу перестановки при рассмотрении подхода Руффини к уравнениям пятой степени. Мы опять видим, как физика основывается на предсуществующих математических открытиях, сделанных в основном «ради самих себя», только потому, что они казались интересными. И снова ключевым ингредиентом является симметрия.

В последних версиях суперструн главной проблемой стал кризис перепроизводства. На смену отсутствию всяких предсказаний пришло производство слишком большого их количества в теории. «Энергия вакуума» — энергетическое содержание пустого пространства — может быть практически любой в зависимости от того, как струны наматываются на дополнительные измерения пространства. Число способов, которыми это может происходить, поистине гигантское — около 10⁵⁰⁰. При различных выборах получаются различные значения энергии вакуума. При этом наблюдаемое значение очень, очень мало — около 10⁻¹²⁰, однако не нулевое.

Согласно стандартной истории с «тонкой настройкой», это конкретное значение как раз подходит для существования жизни. Любое значение, превышающее 10⁻¹¹⁸, заставит локальное пространство-время взорваться; а все меньшее 10⁻¹²⁰ приведет к тому, что пространство-время сожмется и исчезнет в космическом хлопке. Так что «окно возможностей» для жизни очень невелико. Чудесным образом наша вселенная именно в нем и оказалась.

«Слабый антропный принцип» гласит, что если бы наша вселенная не была устроена таким способом, каким она в действительности устроена, то нас бы там не оказалось и мы не задавались бы вопросом о ее устройстве; однако при этом остается открытым вопрос о том, почему нашлось «здесь», в котором мы можем жить. «Сильный антропный принцип» говорит, что мы здесь потому, что вселенная была спроектирована специально для существования в ней жизни, но это — мистическая чепуха. Никто в действительности не знает, какие возможности реализовались бы, если бы вакуумная энергия сильно отличалась от ее актуального значения. Нам известно, что ряд вещей пошел бы вкривь и вкось, но мы и представления не имеем о том, что бы могло появиться вместо них. Большая часть всех аргументов о тонкой настройке — ерунда.

В 2000 году Рафаэль Буссо и Джозеф Полчински предложили иной ответ, используя теорию струн и имеющиеся 10⁵⁰⁰ возможных значений энергии вакуума. Хотя число 10⁻¹²⁰ очень мало, возможные уровни вакуумной энергии отделены друг от друга на 10⁻⁵⁰⁰ единиц, что есть еще меньшее число. Таким образом, большое число теорий струн дает вакуумные энергии в «правильном» интервале. Вероятность, что случайно выбранная энергия попадет в него, по-прежнему пренебрежимо мала, но Буссо и Полчински указали, что это несущественно. В конце концов «правильная» вакуумная энергия непременно возникнет. Идея состоит в том, что вселенная перебирает все возможные теории струн, застревая на каждой до тех пор, пока та не заставит эту вселенную рассыпаться, а затем квантово-механически тунеллирует к некоторой другой теории струн. Если подождать достаточно долго, то на некотором этапе вселенная приобретет вакуумную энергию, которая будет лежать в интервале, подходящем для жизни.

В 2006 году Поль Стайнхардт и Нил Тьюрок предложили вариацию на тему теории тунеллирования — циклическую вселенную, которая расширяется после Большого Взрыва и сжимается в Большом Схлопывании, повторяя такое поведение каждый триллион лет или около того. В их модели энергия вакуума убывает на каждом последовательном цикле, так что в конце концов вселенная получает очень малую, но не нулевую вакуумную энергию.

В той или иной модели вселенная, вакуумная энергия которой достаточно мала, будет тут околачиваться очень долго. Условия пригодны для возникновения жизни, а у жизни полно времени, чтобы развить разум и поинтересоваться, почему она тут оказалась.

Назад: Глава 13 Пятимерный человек

Дальше: Глава 15 Математическая кутерьма

Глава 14 Политический журналист

Глава 14
Политический журналист