Книга: Истина и красота. Всемирная история симметрии.
Назад: Глава 11 Служащий бюро патентов
Дальше: Глава 13 Пятимерный человек
Глава 12
Квантовый квинтет
«Почти все открыто, и все, что остается, — это заполнить несколько пробелов» — не слишком обнадеживающая новость для одаренного молодого человека, намеревающегося изучать физику, в особенности когда такая новость исходит от специалиста, который по долгу службы обязан быть в курсе дела, — в данном случае от профессора физики Филипа фон Йолли.
Дело происходило в 1874 году, и взгляды фон Йолли отражали то, во что верило большинство физиков того времени: физика закончилась. В 1900 году не кто иной, как знаменитый лорд Кельвин, сказал: «В физике нет ничего нового, подлежащего открытию. Остается лишь выполнять все более и более точные измерения».
Заметим, что он также сказал: «Я твердо заявляю, что летающие машины тяжелее воздуха невозможны» и «Высадка на Луну связана со столь сложными проблемами для людей, что их решение может занять еще 200 лет». Биограф Кельвина пишет, что первую половину своей карьеры он был во всем прав, а всю вторую — не прав.
Но он был не совсем не прав. В лекции 1900 года «Тучи XIX столетия над динамической теорией теплоты и света» он указал на два наиболее существенных пробела в современном ему понимании физической вселенной: «Красота и ясность динамической теории, которая утверждает, что теплота и свет являются формами движения, омрачены в настоящее время двумя тучами. Первая — это вопрос о том, как Земля движется через упругое тело, каковым по сути является светоносный эфир. Вторая — это доктрина Максвелла-Больцмана о распределении энергии». Первая туча оказалась предвестницей теории относительности, вторая — предвестницей квантовой теории.
По счастью, молодого адресата рекомендация фон Йолли не отпугнула. Он заявил, что у него нет желания открывать новое — все, чего он хочет, сводится к развитию лучшего понимания известных оснований физики. В поисках такого понимания он произвел одну из двух величайших революций в физике двадцатого столетия и развеял второе из Кельвиновых облаков. Этого человека звали Макс Планк.
Юлиус Вильгельм Планк был профессором права в Киле и Мюнхене. И его отец, и мать были профессорами теологии, а брат — судьей. Так что, когда его вторая жена Эмма Патциг осчастливила его сыном — шестым ребенком, — было заранее ясно, что мальчику предстоит вырасти в интеллектуальной среде. Макс Карл Эрнст Людвиг Планк появился на свет 23 апреля 1858 года.
Европа, как обычно, находилась в состоянии политических неурядиц, и в самых ранних воспоминаниях мальчика сохранился вступление в Киль прусских и австрийских войск во время Датско-Прусской войны 1864 года.
К 1867 году Планки перебрались в Мюнхен, где образование Макса проходило под руководством математика Германа Мюллера в Школе короля Максимилиана. Мюллер учил мальчика астрономии, механике, математике и основам физики, в частности — закону сохранения энергии. Планк был превосходным учеником и закончил учебу необычно рано, в шестнадцатилетнем возрасте.
Кроме того, он был еще и способным музыкантом, однако, несмотря на высказанный с самыми добрыми намерениями совет Йолли, все же решил изучать физику. Планк занимался под руководством Йолли кое-какими экспериментами, но быстро переключился на теоретическую физику. Он познакомился с несколькими физиками и математиками, занимавшими ведущее положение в мире, и в 1877 году переехал в Берлин, где продолжил свое обучение у Гельмгольца, Густава Кирхгоффа и Вейерштрасса. В 1878 году он успешно сдал свои первые экзамены, а в 1879-м защитил диссертацию по термодинамике. В течение некоторого времени он преподавал математику и физику в своей старой школе. В 1880 году он защитил диссертацию на право преподавания в университете, темой которой были равновесные состояния тел при различных температурах, и перед ним открылись перспективы академической карьеры. Со временем он получил соответствующую должность, однако это произошло лишь в 1885 году, когда он стал доцентом в университете в Киле. Его научные интересы были сосредоточены на термодинамике, в особенности на концепции энтропии.
Макс познакомился с Мари Мерк, сестрой одного из своих друзей, и в 1887 году они поженились и стали снимать квартиру. Всего у них было четверо детей: Карл, близнецы Эмма и Грета, а также Эрвин.
В 1889 году — в том самом году, когда родились близнецы — Макс получил в Берлине должность, которую ранее занимал Кирхгофф, а в 1892 году стал полным профессором. Семейство переехало на виллу в берлинском районе Грюневальд, по соседству с другими выдающимися представителями академической среды. Один из них, теолог Адольф фон Харнак, стал близким другом Планков. Планки были общительной семьей, и дома у них регулярно бывали знаменитые интеллектуалы, включая Эйнштейна и физиков Отто Гана и Лизе Майтнер, которые позднее совершили фундаментальные открытия в области деления атомного ядра, послужившие частью долгого пути к созданию атомной бомбы и атомных электростанций. Когда в доме Планков бывали гости, там по заложенной Гельмгольцем традиции исполнялась музыка.
В течение некоторого времени жизнь была безоблачна; но Мари заразилась легочной инфекцией — возможно, туберкулезом — и умерла в 1909 году. Через полтора года, в возрасте пятидесяти двух лет, Макс снова женился — его супругой стала Марга фон Хесслин, родившая ему третьего сына — Германа.
В 1894 году местная электрическая компания пыталась разработать более эффективную лампочку накаливания, так что Макс занялся некоторыми исследованиями по контракту для промышленности. В принципе анализ лампы накаливания представлял собой стандартную физическую задачу, известную как «излучение черного тела», — задачу о том, как излучался бы свет, испущенный полностью неотражающим телом. Такое тело при нагревании излучает свет на всех частотах, но интенсивность света, или, что эквивалентно, его энергия, зависит от частоты. Спрашивалось, как частота влияет на интенсивность. Без ответа на этот фундаментальный вопрос трудно было бы изобрести более эффективную лампочку.
Имелись твердо установленные экспериментальные результаты, а также один теоретический — закон Релея-Джинса, полученный из основополагающих принципов классической физики. К сожалению, этот закон не согласовывался с результатами экспериментов, проводимых для высокочастотного излучения. Он даже предсказывал нечто невозможное: по мере возрастания частоты света его энергия должна становиться бесконечно большой. Этот невозможный результат получил известность как «Ультрафиолетовая катастрофа». Дальнейшие эксперименты привели к формулировке нового закона, который был получен подгонкой под наблюдения за высокочастотным излучением и известен как закон Вина по имени его открывателя Вильгельма Вина.
Однако закон Вина был непригоден для низкочастотного излучения.
Физикам приходилось иметь дело с двумя законами: один из них работал на низких частотах, но не работал на высоких, а другой — в точности наоборот. Планк задался идеей построить интерполяцию между ними — другими словами, записать математическое выражение, которое на низких частотах переходило бы в закон Релея-Джинса, а на высоких — в закон Вина. В результате возникла формула, которую теперь называют законом Планка для излучения черного тела.
Этот новый закон был сознательно устроен таким образом, чтобы прекрасно отвечать экспериментальным наблюдениям во всем спектре электромагнитного излучения, однако он был чисто эмпирическим — т.е. выведенным из эксперимента, а не из каких-либо фундаментальных физических принципов. Планка, действовавшего в согласии со своим намерением лучше понять известные законы физики, это не устраивало, и он потратил значительные усилия на поиск физических принципов, которые могли бы привести к написанной им формуле.
В 1900 году Планк наконец заметил любопытное свойство своей формулы. Ее можно было вывести, практически повторяя вычисления, которые приводили к закону Релея-Джинса, если только сделать там одно маленькое изменение. В классическом выводе предполагалось, что для любой заданной частоты энергия электромагнитного излучения может в принципе принимать любое — какое угодно — значение. В частности, она может приближаться к нулю сколь угодно близко. Планк осознал, что именно это предположение и было причиной ультрафиолетовой катастрофы и что если бы было сделано другое предположение, то проблемы с появлением бесконечности в вычислениях не возникало бы.
Правда, спасительное предположение носило радикальный характер. Требовалось, чтобы энергия излучения на заданной частоте складывалась только из целого числа «пакетов» фиксированного размера. При этом требовалось, чтобы размер каждого пакета был пропорционален частоте, другими словами — равным частоте, умноженной на некоторую постоянную величину; эту постоянную мы сейчас называем постоянной Планка и обозначаем символом h.
Эти пакеты энергии получили название квантов. Планк проквантовал свет.
Отлично, но почему же экспериментаторы никогда не замечали, что энергия выражается целым числом квантов? Путем сравнения своих вычислений с наблюдаемыми энергиями Планк сумел определить величину своей постоянной. Она оказалась очень — очень — маленькой. В действительности h примерно равняется 6×10−34 джоуль-секунд. Грубо говоря, чтобы заметить «дырки» или «скачки» в возможных значениях энергии — т.е. значения, которые классическая физика разрешает, а квантовая физика запрещает, — требуется выполнить наблюдения с точностью до 34-го десятичного знака. Даже сегодня очень немногие физические величины можно измерять с точностью до шести или семи десятичных знаков, а в те дни и три знака были серьезным требованием. Прямое наблюдение кванта требует невероятного уровня точности.
Может показаться странным, что математическое различие, столь тонкое, что его нельзя увидеть, оказывает такой радикальный эффект на закон излучения. Но вывод этого закона включает в себя суммирование по вкладам, вносимым в энергию всеми возможными частотами. Результат представляет собой коллективный эффект всех возможных квантов. Глядя с Луны, нельзя разглядеть отдельную песчинку на Земле. Но Сахара очень даже заметна. Когда складывается вместе достаточно много маленьких вкладов, результат может оказаться огромным.
Планковская физика процветала, но личная жизнь Планка оказалась исполненной трагизма. Его сын Карл погиб на фронте во время Первой мировой войны. Дочь Грета умерла при родах в 1917 году, а Эмма разделила ее судьбу в 1919-м, после того как вышла замуж за овдовевшего мужа сестры. Много позднее Эрвин был казнен нацистами за участие в неудавшемся покушении на Адольфа Гитлера в 1944 году.
К 1905 году появились новые свидетельства, поддерживающие радикальное предложение Планка; они содержались в работе Эйнштейна о фотоэлектрическом эффекте. Напомним, что суть эффекта состоит в том, что свет можно превратить в электричество.
Эйнштейн знал, что электричество существует в виде дискретных пакетов. Действительно, к тому времени физики выяснили, что электричество представляет собой движение мельчайших частиц, называемых электронами. Из фотоэлектрического эффекта Эйнштейн вывел, что то же должно быть верно и в отношении света. Это не только подтверждало идеи Планка о квантах света, но и объясняло, что же такое эти кванты: световые волны, подобно электронам, должны быть частицами.
Как волна может быть частицей? И тем не менее таков был однозначный вывод из экспериментов. Открытие частиц света или фотонов, быстро привело к квантовой картине мира, в которой частицы являются на самом деле волнами, ведущими себя иногда одним способом, а иногда другим.
Физическое сообщество начало относиться к квантам более серьезно. Великий датский физик Нильс Бор выдвинул квантованную модель атома, в которой электроны движутся вокруг центрального ядра по орбитам, представляющим собой окружности, причем размеры окружностей подчинены дискретности квантов. Из того, что фотоны могут быть и волнами, и частицами, а электроны испускаются соответствующими металлами при попадании на них фотонов, французский физик Луи де Бройль заключил, что и электроны также должны быть и волнами, и частицами. На самом деле вся материя должна демонстрировать эту двойственную природу — быть иногда твердыми частицами, а иногда — колеблющимися волнами. Вот почему в эксперименте можно обнаружить то одно, то другое.
На исключительно малых масштабах материю в действительности не описывают ни «частица», ни «волна». Элементарные составные части материи являются немного и тем и другим — частицами-волнами. Де Бройль изобрел формулу для описания частиц-волн.
Далее произошло важнейшее для нашего рассказа событие. Эрвин Шредингер взял формулу де Бройля и превратил ее в уравнение, описывающее движение частиц-волн. Подобно тому как законы движения Ньютона имели фундаментальное значение для классической механики, так и уравнение Шредингера стало фундаментом механики квантовой.
Эрвин Шредингер родился в Вене в 1886 году в результате смешанного брака. Его отец Рудольф Шредингер занимался производством погребальных одежд — навощенных одеяний, используемых на саваны для умерших; он, кроме того, был ботаником. Рудольф был католиком, а мать Эрвина Георгина Эмилия Бренда — лютеранкой. С 1906 по 1910 год Эрвин изучал физику в Вене под руководством Франца Экснера и Фридриха Хазенорля, ставшего ассистентом Экснера в 1911 году. Он защитил диссертацию на право преподавания в 1914-м, в момент начала Первой мировой войны, и провел войну в качестве офицера австрийской артиллерии. Два года спустя после окончания войны он женился на Аннемари Бертель. В 1920 году он занял соответствующую доценту должность в Штутгарте, а с 1921-го стал полным профессором в Бреслау (ныне Вроцлав в Польше).
Уравнение, носящее теперь его имя, Шредингер опубликовал в 1926 году в статье, где показал, что из этого уравнения можно получить правильные уровни энергии для спектра атома водорода. За ней в скором времени последовали три другие ключевые статьи по квантовой теории. В 1927 году он приехал к Планку в Берлин, но в 1933-м из-за антисемитизма нацистов уехал из Германии в Оксфорд, где его приняли в Колледж Магдалины. Вскоре после этого он вместе с Полем Дираком был удостоен Нобелевской премии по физике.
Шредингер вел вызывающий образ жизни, живя одновременно с двумя женщинами, что, конечно, задевало тонкие, чувствительные натуры оксфордских донов.
Не прошло и года, как он снова переехал, на этот раз в Принстон, где ему предложили постоянную работу, но он не стал принимать этого предложения — возможно, из-за того, что его желание жить одной семьей и с женой, и с любовницей вызывало в Принстоне взгляды ничуть не более благосклонные, чем в Оксфорде. В конце концов в 1936 году он осел в австрийском Граце, не обращая внимания на пуританскую нетерпимость австрийцев.
Присоединение Австрии Гитлером создало для Шредингера немалые сложности из-за его известной неприязни к нацистам. Он публично отрекся от своих взглядов (и много лет спустя извинялся за это перед Эйнштейном). Но уловка не сработала: он лишился работы, поскольку считался политически неблагонадежным, и ему пришлось бежать в Италию.
В конце концов Шредингер поселился в Дублине. В 1944 году вышла его книга «Что такое жизнь?» — захватывающая, но неудачная попытка применить квантовую физику к живым организмам. Его идеи основывались на концепции «негэнтропии» — тенденции живого не подчиняться второму закону термодинамики (или как-то обходить его действие). Шредингер подчеркивал, что гены живых существ должны представлять собой некие сложные молекулы, содержащие закодированные инструкции. Эти молекулы теперь называются ДНК, но их структура была открыта только в 1953 году Фрэнсисом Криком и Джеймсом Уотсоном, вдохновленными — отчасти — Шредингером.
В Ирландии Шредингер не изменял своему свободному отношению к сексуальности, вступая в связи со студентками и став отцом двух детей от разных матерей.
Он умер в Вене от туберкулеза в 1961 году.
Более всего Шредингер известен благодаря своему коту. Не настоящему коту, а тому, который участвует в мысленном эксперименте. Его нередко интерпретируют как причину, по которой шредингеровские волны нельзя рассматривать как нечто реально физическое, а надо воспринимать как некое завуалированное описание, которое само по себе проверить невозможно, но из которого проистекают верные следствия. Однако эта интерпретация не вполне последовательна — если волны не существуют, то почему выводимые из них следствия столь хорошо применимы?
Как бы то ни было, вернемся к коту. Согласно квантовой механике, частицы-волны могут интерферировать друг с другом, налагаясь одна на другую и при этом усиливая друг друга в тех случаях, когда пик одной волны попадает на пик другой, или же гася друг друга, когда пик накладывается на провал. Поведение такого типа называется суперпозицией, так что квантовые частицы-волны могут создавать суперпозиции, накладываясь друг на друга, — откуда следует, что они потенциально содержат множество возможных состояний, но при этом не находятся ни в одном из них самом по себе. Согласно Бору и знаменитой «копенгагенской интерпретации» квантовой теории, в этом-то и состоит естественное положение вещей. Только тогда, когда мы производим наблюдение какой-либо физической величины, мы заставляем ее выйти из некоторой квантовой суперпозиции и оказаться в каком-то единственном «чистом» состоянии.
Такая интерпретация хорошо работает для электронов, однако Шредингер задался вопросом о том, что она будет означать для кота. В его мысленном эксперименте запертый в ящике кот может находиться в суперпозиции состояний жизни и смерти. Когда вы открываете ящик, вы совершаете наблюдение над котом и тем самым заставляете его оказаться или в одном состоянии, или в другом. Как заметил в «Маскараде» Терри Пратчетт, коты устроены не так. Кот-супермачо Грибо появляется из ящика в третьем состоянии — до чертиков разъяренным.
Шредингеру тоже было известно, что коты устроены иначе, хотя и по другим причинам. Электрон — микроскопическая вещица и ведет себя тем или иным образом на квантовом уровне. Он обладает (когда мы потрудимся сделать соответствующее измерение) определенной координатой, или скоростью, или спином, описать которые относительно несложно. Кот же — существо макроскопическое, и с ним все по-другому. Можно устроить суперпозицию состояний электрона, но не кота. У нас с женой две кошки, и когда они пытаются устроить суперпозицию, результат состоит из летящей шерсти и двух крайне негодующих кошек. Жаргонное слово здесь — это «декогеренция», которая объясняет, почему в повседневной жизни большие квантовые системы, подобные котам, выглядят как привычные «классические» системы. Декогеренция говорит нам, что кот состоит из столь большого числа частиц-волн, что они все перепутываются и разрушают суперпозицию за время, меньшее, чем свет затрачивает на прохождение расстояния, равного диаметру электрона. Таким образом, коты, являясь макроскопическими системами, состоящими из очень большого числа квантовых частиц, ведут себя как коты. Они могут быть или живыми, или мертвыми, но не могут находиться в обоих этих состояниях сразу.
Тем не менее на достаточно малых масштабах — а мы говорим о вещицах по-настоящему малых, а вовсе не таких, которые можно разглядеть в обычный микроскоп, — вселенная ведет себя в точности так, как ей велит квантовая физика, и ей удается делать две разные вещи в один момент времени. И это все меняет.
Насколько странным должен быть квантовый мир, стало ясно из работ Вернера Гайзенберга. Гайзенберг был блестящим физиком-теоретиком, но его знакомство с экспериментом было столь ничтожным, что на экзамене, необходимом для защиты диссертации, он не смог ответить на простые вопросы о телескопах и микроскопах. Он даже не знал, как работает аккумуляторная батарея.
Август Гайзенберг женился на Анне Велайн в 1899 году. Он был лютеранином, а она — католичкой, и ей пришлось перейти в его религию, для того чтобы их брак состоялся. У них было много общего: он был преподавателем и специалистом по Античности, специализирующимся в древнегреческом, она же была дочерью преподавателя и специалиста по греческим трагедиям. Их первый сын Эрвин родился в 1900 году и стал химиком. Второй — Вернер — родился в 1901-м и изменил мир.
Германия в то время еще была монархией, и профессия преподавателя означала высокий социальный статус, так что Гайзенберги жили в финансовом отношении благополучно и могли отдать своих детей в хорошие школы. В 1910 году Август стал профессором средневекового и современного греческого языка в Мюнхенском университете, и семья переехала в этот город. В 1911 году Вернер начал обучение в Школе короля Максимилиана в Мюнхене, где до этого учился и Планк. Дед Вернера Николаус Велайн был директором школы. Мальчик рос сообразительным и живым, отчасти из-за того, что его отец побуждал его соперничать со старшими, и демонстрировал замечательные способности к математике и естественным наукам. Он был, кроме того, одарен еще и музыкально и освоил фортепиано столь хорошо, что в 12-летнем возрасте выступал на школьных концертах.
Позднее Гайзенберг писал, что его «интерес и к языкам, и к математике проснулся достаточно рано». Он получал высшие оценки по греческому и латыни и хорошо учился по математике, физике и религии. Худшими для него предметами были физкультура и немецкий. У него был превосходный учитель математики по имени Кристоф Вольф, который развивал способности Вернера, давая ему решать специальные задачи. Скоро ученик превзошел учителя, и в школьной характеристике Гайзенберга было сказано: «Его независимая работа в области математики и физики далеко выходит за школьные требования». Он самостоятельно изучил теорию относительности, отдавая предпочтение ее математическому содержанию перед физическими следствиями. Когда родители попросили его позаниматься со студенткой из местного колледжа, чтобы подготовить ее к экзаменам, он самостоятельно освоил математический анализ — предмет, не входящий в школьную программу. В нем развился интерес к теории чисел, про которую он говорил, что «она понятна, там все устроено так, что можно понять все до самого конца».
Чтобы помочь Вернеру совершенствоваться в латыни, отец принес ему кое-какие старые статьи по математике, написанные на этом языке. Среди них была диссертация Кронеккера, посвященная некоторому разделу («комплексные единицы») алгебраической теории чисел. Кронеккер — мирового уровня специалист по теории чисел — знаменит своей верой, что «Господь сотворил целые числа, а все остальное — дело рук человека». Гайзенберг так воодушевился, что даже предпринял попытку доказательства Последней теоремы Ферма. Проведя в школе девять лет, он закончил ее первым учеником в своем классе и поступил в Мюнхенский университет.
Когда разразилась Первая мировая война, союзники блокировали Германию. Еды и топлива не хватало; школу пришлось закрыть, потому что ее нечем было отапливать, и как-то раз Вернер так ослабел от голода, что свалился с велосипеда в канаву. Отец и учителя сражались на фронте; молодые люди, остававшиеся в тылу, проходили военную подготовку и подвергались националистической обработке. Конец войны принес с собой и конец немецкой монархии, и Бавария на короткое время приобрела социалистическое правительство в советском духе, но в 1919 году пришедшие из Берлина немецкие войска выбили социалистов и восстановили более умеренную социальную демократию.
Как и большая часть его поколения, Вернер расстался с иллюзиями после поражения Германии и обвинял старших в военной неудаче. Он стал вожаком группы, связанной с Новой Молодежью — экстремистской организацией правого толка, которая ставила своей целью восстановление монархии и мечтала о Третьем Рейхе. Многие отряды Новой Молодежи были антисемитскими, но в группу Вернера входило несколько еврейских мальчиков. Он проводил много времени с этими ребятами, устраивая с ними походы и экскурсии и в целом пытаясь воссоздать романтическое представление о Германии, какой она некогда была, но эти мероприятия прекратились в 1933 году, когда когда Гитлер запретил все молодежные организации, кроме учрежденных им самим.
В 1920 году Вернер прибыл в Мюнхенский университет, намереваясь стать чистым математиком, пока собеседование с одним из профессоров чистой математики не отвратило его от этой идеи. Вместо этого он решил изучать физику под руководством Арнольда Зоммерфельда. Мгновенно оценив способности Вернера, Зоммерфельд позволил ему посещать лекции для старшекурсников. Вскоре Вернер выполнил оригинальное исследование, посвященное квантовому подходу к строению атома. Диссертацию он защитил в 1923 году, побив университетский рекорд скорости. В том же году Гитлер предпринял попытку свергнуть правительство Баварии, получившую название «пивной путч» и задуманную как прелюдия марша на Берлин, однако попытка эта провалилась. Свирепствовала безудержная гиперинфляция, Германия рассыпалась.
Вернер продолжал работать. Он сотрудничал со многими ведущими физиками — все они размышляли о квантовой теории, поскольку именно в этой области и происходило все самое главное. Он работал ассистентом Макса Борна, пытаясь создать улучшенную теорию атома. Гайзенбергу пришло в голову представлять состояния атома в терминах частот, наблюдаемых в его спектре, — т.е. в терминах того вида света, который мог испускаться атомом. Идею эту он развил до уровня некоторой занятной математики, оперирующей списками чисел. Борн в какой-то момент осознал, что списки такого типа представляют собой нечто вполне добропорядочное; математики называют их матрицами. Обрадованный тем, что его идеи оказались осмысленными, Борн отправил статью в печать. По мере своего развития эти идеи вызревали в новую, последовательную математику квантовой теории — матричную механику. Она воспринималась как конкурент шредингеровской волновой механики.
Кто же был прав? Оказалось, что две теории тождественны друг другу. Это в 1926 году обнаружил Шредингер. Они были просто двумя различными математическими представлениями одних и тех же базисных концепций, подобно тому как эвклидовы методы и алгебра дают два эквивалентных способа смотреть на геометрию. Сначала Гайзенберг не мог этому поверить, поскольку суть его матричного подхода состояла в нарушении непрерывности — в существовании прыжков, которыми электрон изменяет свое состояние. Элементы в его матрицах были связаны с изменениями энергии. Он никак не мог понять, как волны — непрерывные сущности — могут моделировать скачки (т.е. разрывы). В письме к австро-швейцарскому физику Вольфгангу Паули он писал: «Чем больше я думаю о физической части теории Шредингера, тем более отталкивающей я ее нахожу… То, что Шредингер пишет о возможности наглядного представления своей теории — „вероятно, не совсем верно“, — другими словами — чушь». В действительности эти разногласия были частью гораздо более давнего спора, в котором Бернулли и Эйлер расходились по вопросу о решениях волнового уравнения. У Бернулли была формула для решений, но Эйлер не мог понять, как эта формула, выглядевшая непрерывной, иногда умудрялась давать разрывные решения. Тем не менее Бернулли был прав — как и Шредингер. Пусть его уравнения непрерывны, но многие свойства их решений могут оказаться дискретными — случай, к которому относятся и уровни энергии.
Большинство физиков высказывались в пользу картины волновой механики, потому что она более понятна интуитивно. Матрицы же были немного слишком абстрактными. Гайзенберг по-прежнему предпочитал свои списки, потому что они были составлены из наблюдаемых величин, тогда как экспериментально зарегистрировать какую-нибудь шредингеровскую волну не представлялось возможным. В действительности копенгагенская интерпретация квантовой теории, драматизированная участием в ней шредингеровского кота, утверждала, что всякая попытка зарегистрировать шредингеровскую волну приведет к «коллапсу» волны в уединенный пик. Так что Гайзенберг проявлял все большую и большую озабоченность тем, как и какие аспекты квантового мира можно измерять. Каждый элемент из его списков можно измерить. С одной шредингеровской волной этого сделать нельзя. Гайзенберг воспринял это различие как серьезнейшую причину сделать выбор в пользу матриц.
Следуя такой логике рассуждений, он обнаружил, что в принципе можно измерить координату частицы с любой желаемой точностью — но за это придется заплатить высокую цену, потому что чем более точно мы знаем координату частицы, тем менее точно мы можем знать ее импульс. И наоборот, если удалось измерить импульс с очень высокой точностью, то теряется информация о координате. Тот же баланс имеет место в отношении энергии и времени. Можно измерить или одно, или другое, но не то и другое вместе — если, конечно, нужны высокоточные измерения.
И проблема лежала вовсе не в области применяемых экспериментальных процедур; таково свойство, внутренне присущее квантовой теории. Гайзенберг изложил свою аргументацию в письме к Паули в феврале 1927 года. Письмо в конце концов переросло в статью, и идея Гайзенберга получила название принципа неопределенности. Этот принцип представлял собой один из первых примеров внутренних ограничений, присущих физике. Другой пример — это утверждение Эйнштейна о том, что ничто не может двигаться быстрее света.
В 1927 году Гайзенберг стал самым молодым в Германии профессором, и произошло это в Лейпцигском университете. В 1933 году — том самом, когда Гитлер пришел к власти — Гайзенберг получил Нобелевскую премию по физике. Это сделало его чрезвычайно влиятельной фигурой, а его желание остаться в Германии во времена нацистского режима заставило многих думать, что Гайзенберг и сам был нацистом. Насколько можно судить, это не так. Но он был патриотом, и это привело его к связи с нацистами и к невольному соучастию во многих их действиях. Имеются свидетельства, что Гайзенберг пытался помешать властям, когда они принялись изгонять евреев с университетских должностей, но эффекта его попытки не возымели. В 1937 году о нем отзывались как о «белом еврее», и он находился под угрозой отправиться в концентрационный лагерь, но через год с него снял подозрения Генрих Гиммлер — глава СС. В том же 1937 году Гайзенберг женился на Элизабет Шумахер, дочери экономиста. Их первыми отпрысками были близнецы; всего они произвели на свет семерых детей.
Во время Второй мировой войны Гайзенберг был одним из главных физиков, занимавшихся созданием в Германии ядерного оружия — атомной бомбы. Он работал на ядерных реакторах в Берлине, в то время как жена и дети отправились в Баварию, в летний дом их семьи. Роль Гайзенберга в немецком атомном проекте оказалась весьма неоднозначной. Когда война закончилась, его арестовали британцы и в течение шести месяцев допрашивали в сельском доме недалеко от Кембриджа. Протоколы его допросов, недавно ставшие доступными, лишь углубили полемику. Гайзенберг заявляет, что его интересы ограничивались созданием ядерного реактора («engine»), и он не собирался участвовать в создании бомбы: «Я бы сказал, что у меня не вызывала сомнений наша способность создать урановый реактор, но я никогда не думал, что мы сделаем бомбу, и в глубине своего сердца я даже был рад, что речь шла о реакторе, а не о бомбе. Должен это признать». Правдивость этого заявления до сих пор горячо дебатируется.
После войны, отпущенный из британского заключения, Гайзенберг вернулся к работам по квантовой теории. Он умер от рака в 1976 году.
Немецкие создатели квантовой теории в большинстве своем происходили из интеллектуальной среды — они были детьми врачей, юристов, ученых или представителей других подобных профессий. Они жили в дорогих домах, играли на музыкальных инструментах и участвовали в текущей социальной и культурной жизни. Великому английскому создателю квантовой механики выпало совсем иное и куда более печальное детство — деспотичный и определенно неуравновешенный отец, оторванный от собственных родителей, да и от всей своей семьи, и мать, настолько забитая и запуганная, что она с двумя детьми ела на кухне, пока муж и младший сын в полном молчании обедали в столовой.
Отец — Шарль (Чарльз) Адриен Ладислас Дирак — родился в швейцарском кантоне Вале в 1866 году и в 20-летнем возрасте сбежал из дома. Чарльз прибыл в Бристоль в 1890 году, но стал британским подданным лишь в 1919-м. В 1899 году он женился на дочери морского капитана Флоренс Ханне Холтен, и на следующий год появился на свет их первенец Реджинальд. Два года спустя к семейству прибавился Поль Адриен Морис; еще через четыре года родилась дочь Беатрис.
До 1905 года (когда он поехал навестить мать в Швейцарии — через десять лет после смерти отца) Чарльз не сообщал родителям ни о своей женитьбе, ни о том, что у них есть внуки.
Чарльз преподавал в Торгово-Техническом колледже в Бристоле. В целом он считался неплохим преподавателем, но, кроме того, славился полным отсутствием человеческих чувств и чрезвычайной строгостью и требовательностью. Он был ревнителем строжайшей дисциплины и муштры, но такими были тогда многие преподаватели.
Поль — интроверт от природы — стал еще более выраженным интровертом в силу странной отчужденности отца и отсутствия всякого общения. Чарльз требовал, чтобы Поль говорил с ним только по-французски, расчитывая таким образом подтолкнуть ребенка к изучению этого языка. Поскольку Поль говорил по-французски очень плохо, он предпочитал не говорить вовсе. Вместо этого он проводил долгие часы, размышляя о мире природы. Не способствующее общению устройство трапез в доме Дираков также, по-видимому, проистекало из правила, что разговор должен вестись исключительно по-французски. Так и осталось неясным, активно ли ненавидел Поль своего отца или же просто недолюбливал, но когда Чарльз умер, главное ощущение Поля выражалось словами: «Теперь я чувствую себя намного свободнее».
Чарльз гордился интеллектуальными способностями Поля и питал немалые амбиции в отношении своих детей — имея при этом в виду, что они будут делать в жизни то, что он для них распланировал. Когда Реджинальд сказал, что хочет быть врачом, Чарльз настоял, чтобы он стал инженером. В 1919 году Реджинальд с трудом получил диплом инженера; через пять лет, работая над инженерным проектом в Вулверхэмптоне, он покончил с собой.
Поль жил дома с родителями и также изучал инженерное дело — в том же колледже, что и его брат. Его любимым предметом была математика, но он решил не посвящать себя ее изучению. Возможно, он не хотел идти против воли отца; но, помимо этого, он находился под воздействием ложного впечатления — достаточно распространенного до сих пор, — что единственное, к чему может привести карьера математика, — это преподавание в школе. Никто не сказал ему, что существуют и другие возможности, и одна из них — исследовательская работа.
Спасение явилось в форме газетного заголовка. Первая страница Times за 7 ноября 1919 года пронзительно возглашала:
Революция в науке. Новая теория Вселенной. Идеи Ньютона ниспровергнуты.
Посередине второй колонки красовался подзаголовок Пространство «покоробилось». Внезапно все стали говорить о теории относительности.
Напомним, что, согласно одному из предсказаний общей теории относительности, гравитация искривляет траекторию распространения света, причем на величину, вдвое превышающую ту, что предсказывается ньютоновскими законами. Фрэнк Дайсон и сэр Артур Стенли Эддингтон предприняли экспедицию на остров Принсипе у побережья Западной Африки, где предстояло наблюдать солнечное затмение.
Одновременно Эндрю Кроммлин из Гринвичской обсерватории возглавил вторую экспедицию в Собрал в Бразилии. Оба отряда наблюдали звезды вблизи края солнечного диска во время полного солнечного затмения и обнаружили легкие сдвиги в кажущихся положениях звезд, согласующиеся с предсказанием Эйнштейна, но не с предсказанием ньютоновской механики.
Эйнштейн, проснувшийся знаменитым, послал своей матери открытку такого содержания: «Дорогая мама, сегодня радостная новость. X.А. Лоренц телеграфировал, что английские экспедиции действительно доказали отклонение света Солнцем». Дирак заглотил наживку: «Меня захватило всеобщее возбуждение, вызванное теорией относительности. Мы постоянно об этом говорили. Студенты обсуждали ее между собой, однако имелось слишком мало точной информации для того, чтобы двигаться дальше». Общественное знание о теории относительности по большей части сводилось к словам; философы утверждали, что они уже многие годы знали, что «все на свете относительно», и выказывали пренебрежение к новой физике, как к старой шляпе. К сожалению, они лишь выставляли напоказ свое невежество и легковерность, с которой они переняли некорректную терминологию.
Поль сходил на несколько лекций по теории относительности, прочитанных Чарли Броудом, который в то время был профессором философии в Бристоле, но математическое содержание этих лекций его не удовлетворило. В конце концов он купил экземпляр эддингтоновской книги «Пространство, время и тяготение» и самостоятельно освоил необходимые разделы математики и физики. Еще до своего отъезда из Бристоля он досконально изучил и специальную, и общую теории относительности.
Полю хорошо давалась теория, зато лабораторные работы были для него кошмаром. Позднее физики стали говорить об «эффекте Дирака»: стоило только ему войти в лабораторию, как все эксперименты там начинали выходить из-под контроля. Мир инженерных наук для него означал бы катастрофу. Он получил блестящий диплом, но некоторое время оставался безработным, поскольку это было время послевоенной экономической депрессии. По счастью, ему представилась возможность изучать математику в Бристольском университете, причем за обучение уже было заплачено, и он ухватился за этот шанс. Его специализацией стала прикладная математика.
В 1923 году Поль стал аспирантом в Кембриджском университете, где столкнулся с серьезными проблемами из-за своей застенчивости. Он не интересовался никакими видами спорта, неохотно заводил друзей и всячески избегал женщин. Время он проводил главным образом в библиотеке. Еще в 1920 году он проработал все лето на той же фабрике, что и его брат Реджинальд. Два брата периодически встречались на улице, но часто проходили друг мимо друга, не останавливаясь, чтобы перекинуться парой слов, — настолько укоренилась семейная привычка к молчанию.
Поль быстро стал заметной фигурой; за шесть месяцев исследований он написал свою первую научную работу. Бурным потоком за ней последовали другие. Именно тогда, в 1925 году, он и столкнулся с квантовой механикой. Во время одной из долгих осенних прогулок по окрестностям Кембриджа он вдруг задумался о гайзенберговских «списках». Они представляют собой матрицы, а матрицы не коммутируют — обстоятельство, которое изначально не давало покоя Гайзенбергу. Дираку была известна идея Ли, что в такой ситуации важную роль играет не произведение AB, а коммутатор AB − BA, и он всерьез заинтересовался захватывающей идеей, что некий весьма похожий объект имеется в гамильтоновом формализме описания механики, где он называется скобкой Пуассона. Но Дирак никак не мог вспомнить соответствующую формулу.
Мысли об этом занимали его почти всю ночь, а на утро он «поспешил в одну из библиотек, прямо к моменту ее открытия, и там посмотрел в уитгекеровской „Аналитической динамике“, как выглядит скобка Пуассона; оказалось, это было именно то, что требовалось». Его открытие состояло вот в чем: коммутатор двух квантовых матриц равен скобке Пуассона соответствующих классических переменных, умноженной на постоянную, равную ih/(2π). Здесь h — постоянная Планка, i — это √−1, а π — ну, это, конечно, π.
Это было впечатляющее открытие. Оно говорило физикам, как надо превращать классические механические системы в квантовые. Стоящая за этим математика была необычайно элегантна — она соединяла две глубокие, но до того момента никак не связанные теории. На Гайзенберга это произвело впечатление.
Вклад Дирака в квантовую теорию разнообразен, и я выберу лишь одно из высших его достижений — релятивистскую теорию электрона, создание которой относится к 1927 году. К тому времени теоретики, занимавшиеся квантовой физикой, знали, что электроны обладают спином, который представляет собой нечто аналогичное моменту вращения мячика вокруг своей оси, однако характеризуется некоторыми весьма странными свойствами, которые делают эту аналогию далеко не полной. Если взять вращающийся мячик и повернуть систему на полные 360°, то и мяч, и момент его вращения окажутся в тех же положениях, которые они занимали до поворота. Однако если вы сделаете то же самое с электроном, то спин его изменит свой знак. Чтобы спин вернулся в первоначальное положение, поворачивать надо на 720°.
Это в действительности довольно сильно напоминает кватернионы, интерпретация которых как «вращений» пространства включает тот же выверт. На математическом языке, вращения пространства образуют группу SO(3), но соответствующая группа в случае кватернионов, как и в случае электронов, есть SU(2). Эти две группы почти одинаковы, только SU(2) «в два раза больше» — она в некотором смысле построена из двух экземпляров группы SO(3). Такое явление называется «двулистным накрытием», из-за чего вращение на 360° и отвечает вращению на удвоенный угол.
Дирак не использовал кватернионы, да и группами не пользовался. Но в конце 1927 года, к наступлению Рождества, он предложил свои спиновые матрицы, которые играют ту же самую роль. Позднее математики обобщили матрицы Дирака на спиноры, которые оказались очень важными в теории представлений групп Ли.
Спиновые матрицы позволили Дираку сформулировать релятивистскую квантовую модель электрона. Из модели получалось все, ради чего она создавалась, и даже немного больше. Наряду с ожидаемыми решениями с положительной энергией она предсказывала решения с отрицательной энергией. Анализируя это парадоксальное свойство, Дирак в конце концов, отбросив несколько неудачных идей, пришел к концепции «антиматерии» — т.е. к идее о том, что всякая частица имеет соответствующую античастицу с той же массой, но с противоположным зарядом. Античастица электрона представляет собой позитрон; он не был известен, пока Дирак не предсказал его существование.
Законы физики остаются (почти) неизменными, если заменить каждую частицу на ее античастицу — такая операция является симметрией природы. Дирак, на которого теория групп никогда не производила особенно большого впечатления, открыл одну из наиболее пленительных групп симметрии в природе.
После 1935 года и до момента своей смерти (в Таллахаси в 1984 году) Дирак придавал огромное значение математическому изяществу физических теорий и в своей работе использовал этот принцип в качестве основополагающего. То, что не является прекрасным, считал он, не может быть верным. В 1956 году, во время посещения Московского государственного университета, следуя традиции записывать мудрые слова на доске, дабы они сохранились для потомства, он написал: «Физический закон должен обладать математической красотой». И он говорил о «высоком математическом качестве» природы. Однако похоже, что теорию групп он никогда не считал прекрасной, быть может, из-за того, что подход физиков к группам, как правило, включает в себя громоздкие вычисления. Лишь математики, как представляется, оказались настроенными на изысканную красоту групп Ли.
Прекрасна она или нет, но благодаря сыну одного кожевника теория групп вскоре заняла свое место среди основных предметов, которые следовало изучать всякому подающему надежды квантовому теоретику.
На рубеже двадцатого столетия кожевенное дело было серьезным занятием (да, собственно, таким и остается). В те дни, однако, даже небольшое предприятие по дублению и продаже кожи могло приносить своему хозяину очень неплохой доход. Хорошим примером такого хозяина был Антал Вигнер, возглавлявший сыромятную мастерскую. Он и его жена Эрсебет были еврейского происхождения, однако не практиковали иудаизм. Они жили в государстве, которое тогда называлось Австро-Венгрией, в городе Пешт. После соединения с соседней Будой он превратился в современный Будапешт — столицу Венгрии.
Второй из трех их сыновей, Йена Паал Вигнер, родился в 1902 году и в возрасте от пяти до десяти лет обучался дома, у частного учителя. Вскоре после начала школьных занятий у Йены обнаружили туберкулез и отправили на лечение в австрийский санаторий. Он пробыл там шесть недель, прежде чем выяснилось, что диагноз неверный. (Окажись он правильным, мальчик, скорее всего, не дожил бы до зрелого возраста.)
Поскольку мальчика заставляли почти постоянно лежать, он занимал себя решением математических задач, просто чтобы убить время. «Мне приходилось дни напролет лежать в шезлонге, — писал он позднее, — и я отчаянно пытался придумать, как построить треугольник по трем заданным высотам». Высоты треугольника — это три линии, которые проходят через вершину и пересекают противоположную сторону под прямым углом. Если треугольник дан, то найти его высоты легко. Решить обратную задачу определенно труднее.
После выписки из санатория Йена продолжал размышлять о математике. В 1915 году он поступил в Лютеранскую гимназию в Будапеште, где в то время уже учился другой мальчик, которому предстояло стать одним из ведущих мировых математиков, — Янош (позднее — Джон) фон Нейман. Однако из знакомство оставалось лишь весьма поверхностным, поскольку фон Нейман предпочитал держаться особняком.
В 1919 году Венгрию наводнили коммунисты, и Вигнеры бежали в Австрию, вернувшись в Будапешт позднее, в том же году, когда коммунистов оттуда выбили. Все семейство перешло в лютеранство, но на Йену это большого влияния не оказало — как он говорил позднее, потому что он был «лишь умеренно религиозен». В 1920 году Йена закончил школу одним из лучших в классе. Он намеревался стать физиком, но отец хотел, чтобы он вступил в семейный кожевенный бизнес. Поэтому вместо того, чтобы получить диплом по физике, Йена стал изучать химическую инженерию: отец полагал, что она будет способствовать бизнесу. Он поступил на первый курс Будапештского технического института, а потом перешел в Высшую техническую школу в Берлине. В конце концов он стал проводить большую часть ценного времени в химической лаборатории, где ему нравилось, и меньшую часть — на теоретических занятиях.
Тем не менее Йена не оставлял мыслей о физике. Берлинский университет находился неподалеку, а кого там можно было увидеть, как не Планка и Эйнштейна вкупе с другими знаменитостями? Йена не преминул воспользоваться этой географической близостью и стал ходить на лекции бессмертных. Он закончил свою диссертацию об образовании и распаде молекул и, как и планировалось, начал работать на кожевенном заводе. Как и следовало ожидать, идея оказалась не слишком удачной. «Дела мои в дубильне шли не очень хорошо… Я чувствовал себя там не в своей тарелке… У меня не было ощущения, что это моя жизнь». Его жизнью были математика и физика.
В 1926 году с ним связался кристаллограф из Института Кайзера Вильгельма, которому требовался ассистент. Обязанности соединяли в себе в химическом контексте оба основных интереса Вигнера. Эта работа оказала огромное влияние на его карьеру, а тем самым и на развитие ядерной физики, поскольку познакомила Вигнера с теорией групп — математикой симметрии.
Первые существенные применения теории групп к физике состояли в классификации всех 230 возможных кристаллических структур. Вигнер писал: «Я получил письмо от кристаллографа, который хотел найти ответ на вопрос, почему положения, которые занимают атомы в кристаллической решетке, соответствуют осям симметрии. Кроме того, он сказал мне, что это должно иметь отношение к теории групп и что мне следует прочитать книгу по теории групп, а после этого найти ответ и сообщить ему».
Возможно, Антал Вигнер был в не меньшем ужасе, чем его сын, от сомнительных успехов последнего в области кожевенного дела, а потому позволил ему стать асситентом кристаллографа. Йена начал с чтения нескольких статей Гайзенберга по квантовой теории и развил теоретический метод вычисления спектра атома с тремя электронами. Он также понял, что этот метод может стать невероятно сложным, когда число электронов превысит три. В этот момент он обратился за советом к своему старому знакомому фон Нейману, который предложил ему почитать о теории представлений групп. Эта область математики в избытке содержала известные в то время алгебраические концепции и сложные методы, в особенности — матричную алгебру. Однако благодаря своим занятиям кристаллографией и близкому знакомству с основным на тот момент учебником по алгебре — Lehrbuch der Algebra Генриха Вебера — Вигнер преодолел матрицы без проблем.
Совет фон Неймана оказался очень хорош. Если атом обладает некоторым числом электронов, то, поскольку все электроны тождественны, атом «не знает», какой электрон какой. Другими словами, уравнения, описывающие излучение, испущенное данным атомом, должны быть симметричны относительно всех перестановок его электронов. Используя теорию групп, Вигнер разработал теорию спектра атомов с любым числом электронов.
До этого момента его работа шла в традиционном русле классической физики. Но все по-настоящему захватывающее творилось в квантовой теории. Тогда Вигнер и принялся за главный труд своей жизни — применение теории представлений групп к квантовой механике.
Занятно, что занимался он этим несмотря на свою новую работу, а не благодаря ей. Мэтр немецкой математики Давид Гильберт выказывал живой интерес к математическим принципам, лежащим в основе квантовой теории, и ему в работе требовался ассистент. В 1927 году Вигнер отправился в Геттинген и был принят там в возглавляемую Гильбертом исследовательскую группу. По идее, его роль должна была состоять в том, чтобы поддерживать связь с физикой, которая подпитывала бы обширные математические таланты Гильберта. На деле же получилось не совсем так, как задумывалось. Гильберт и Вигнер виделись за год всего пять раз. Гильберт был уже стар, утомлен и все более склонялся к уединению. Так что Вигнер вернулся в Берлин, прочитал лекции по квантовой механике и продолжил работу над своей самой знаменитой книгой «Теория групп и ее применения к квантовой механике атомных спектров».
Его частично предвосхитил Герман Вейль, также написавший книгу о группах в квантовой теории. Но основной интерес Вейля концентрировался на фундаментальных вопросах, тогда как целью Вигнера было решение конкретных физических задач. Вейль гнался за красотой, а Вигнер искал истину.
Подход Вигнера к теории групп можно понять в простом классическом контексте — на примере колебаний барабана. Музыкальные барабаны, как правило, округлые, но в принципе могут быть любой формы. При ударе палочкой мембрана барабана начинает вибрировать и создает звук. Барабаны различных форм производят различные звуки. Полоса частот, которые может создать данный барабан, называемая его спектром, сложным образом зависит от его формы. Если барабан симметричен, то можно ожидать, что симметрия появится и в его спектре. Она там и появляется, но довольно тонким образом.
Представим себе прямоугольный барабан — из числа тех, какие нечасто увидишь за пределами математических факультетов. Типичные колебания такого барабана разбивают его поверхность на некоторое число меньших прямоугольников, как, например, показано на рисунке.
На рисунке мы видим различные картины колебаний с двумя различными частотами. Это мгновенные снимки этих колебаний. Темные области смещены вниз, а светлые — вверх.

Две картины колебаний прямоугольного барабана.
Из симметрий барабана вытекают следствия для картин колебаний, поскольку любое преобразование симметрии барабана можно применить к любой возможной картине колебаний, что даст другую возможную картину колебаний. Таким образом, каждая картина колебаний включается в набор других, связанных с ней в соответствии с симметрией. Однако каждая отдельная картина колебаний не обязана иметь те же симметрии, что и барабан. Например, прямоугольник симметричен относительно вращения на 180°. Если применить это преобразование симметрии к двум приведенным выше картинам, они примут вид, показанный на рисунке.
Левая картина не изменилась, так что она, как и барабан, обладает симметрией относительно данного вращения. Но на правой темные и светлые области поменялись местами. Этот эффект называется спонтанным нарушением симметрии, и он очень распространен в физических системах: он возникает, когда в симметричной системе имеются состояния с более низкой симметрией. Левая картина не нарушает симметрии, а правая — нарушает. Посмотрим внимательно на правую картину и разберемся, что следует из ее нарушенной симметрии.
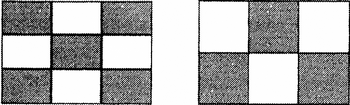
Те же две картины колебаний прямоугольного барабана после поворота барабана на 180°.
Хотя исходная картина и результат ее поворота не совпадают, обе осуществляют колебания на одной и той же частоте, поскольку поворот является симметрией барабана, а следовательно, и тех уравнений, которые описывают его колебания. Поэтому спектр колебаний барабана содержит данную конкретную частоту «два раза». Может показаться, что это трудно наблюдать экспериментально, но если слегка модифицировать барабан, так, чтобы нарушить его вращательную симметрию — скажем, сделать небольшую вмятину вдоль одного из краев, — то две данные частоты начнут слегка отличаться друг от друга, и тогда мы сможем заметить наличие двух очень близких частот. Такого не случилось бы, если бы данная частота содержалась в симметричном барабане только один раз.
Вигнер понял, что тот же эффект возникает для симметричных молекул, атомов и атомных ядер. Звуки, издаваемые барабаном, становятся здесь колебаниями молекул, а спектр звуков заменяется на спектр испущенного или поглощенного света. В квантовом мире спектр создается переходами между состояниями с различными энергиями, и атом излучает фотоны, энергия которых (а потому, как учит нас Планк, и частота) соответствует разнице этих энергий. А спектр можно детектировать, используя спектроскоп. И опять же, некоторые из частот — наблюдаемые в виде спектральных линий — могут оказаться двойными (или имеющими более высокую кратность) в силу симметрии, которой обладают молекула, атом или ядро.
Как детектировать это кратности? В отличие от барабана в молекуле нельзя сделать вмятину. Но можно поместить молекулу в магнитное поле. Оно также разрушает исходную симметрию и приводит к расщеплению спектральных линий. Далее можно использовать теорию групп — точнее, теорию представлений групп — для вычисления частот и того, как они расщепляются.
Теория представлений — одна из самых прекрасных и мощных математических теорий, но она также предъявляет высокие технические требования и содержит множество скрытых ловушек. Вигнер превратил ее в высокое искусство. Другие пытались следовать за ним по пятам.
В 1930 году американский Институт высших исследований в Принстоне предложил Вигнеру работу по совместительству, и он начал курсировать между Принстоном и Берлином. В 1933 году нацисты провели закон, запрещавший евреям работать в университетах, так что Вигнер перебрался в Соединенные Штаты на постоянное жительство — собственно в Принстон, где он поменял свое имя на англизированный вариант — Юджин Пол. Его сестра Маргит приехала к нему в Принстон и познакомилась с Дираком, находившимся там с визитом. В 1937 году, к изумлению многих, они поженились.
С браком Маргит все было хорошо, зато с работой Юджина — нет. В 1936 году Вигнер писал: «Из Принстона меня выгнали. Никто не объяснил почему. Трудно представить, насколько я зол». В действительности Вигнер сам написал заявление об уходе — по-видимому, потому, что его карьерный рост происходил недостаточно быстро. Можно предположить, что отказ Принстонского института продвигать его дальше был им воспринят как завуалированное предложение подать в отставку, так что он верил в то, что его выгнали.
Он быстро нашел новую работу в университете Висконсина, принял гражданство США и познакомился со студенткой-физиком по имени Амелия Франк. Они поженились, но в течение года Амелия умерла от рака.
В Висконсине Вигнер переключился на исследование ядерных сил и обнаружил, что ими управляет группа симметрии SU(4). Он также сделал фундаментальное открытие, относящееся к группе Лоренца, опубликовав его в 1939 году.
Однако в то время теория групп не была стандартной частью образования физика, и ее основными применениями оставались довольно специальные области кристаллографии. Для большинства физиков теория групп выглядела и сложной, и непривычной — сочетание достаточно фатальное. Квантовые физики, пришедшие в ужас от того, что свалилось им на голову, описывали происходящее как Gruppenpest, т.е. групповую заразу. Вигнер вызвал эпидемию, а его коллеги не желали заражаться. Однако взгляды Вигнера оказались пророческими. Теоретико-групповые методы заняли доминирующее положение в квантовой механике, поскольку влияние симметрии оказалось всепроникающим.
В 1941 году Вигнер женился во второй раз, на учительнице по имени Мари Эннетт. У них родились двое детей, Дэвид и Марта. Во время войны Вигнер, как и фон Нейман, вместе со многими ведущими математическими физиками работал над Манхэттенским проектом — созданием атомной бомбы. Ему была присуждена Нобелевская премия по физике в 1963 году.
Несмотря на долгие годы жизни в США, Вигнер неизменно скучал по своей родине. «После 60 лет в Соединенных Штатах, — писал он в старости, — я все еще более венгр, нежели американец. Американская культура по большей части от меня далека». Он умер в 1995 году. Физик Абрахам Пейс описывал его как «очень странного человека… одного из гигантов физики двадцатого столетия». Развитые им подходы заодно произвели революцию и в двадцать первом столетии.
Назад: Глава 11 Служащий бюро патентов
Дальше: Глава 13 Пятимерный человек

