Книга: Мир многих миров. Физики в поисках иных вселенных.
Назад: Глава 7 Антигравитационный камень
Дальше: Глава 9 Говорящие небеса
Глава 8
Вечная инфляция
Я думаю, самый вероятный ответ на вопрос о том, что было до инфляции, — еще большая инфляция.Алан Гут
Вселенная за горизонтом
Что лежит за нашим сегодняшним горизонтом? Этот вопрос занимал меня с самых первых дней знакомства с инфляцией. Если нам видна лишь крошечная часть Вселенной, то какова же ее общая картина — вроде того вида нашей планеты, что открывается космическому путешественнику, когда его корабль удаляется от Земли?
Теория возмущений плотности давала об этом некоторое представление. В соответствии с нею рисунок распределения галактик в пространстве определяется квантовыми флуктуациями, которые испытывало скалярное поле во время инфляции. Этот процесс был случайным, и потому некоторые области такого же размера, как наша, содержат больше галактик, а другие — меньше. Причина, по которой галактика Млечный Путь находится именно здесь, состоит в том, что скалярное поле в этом месте едва заметно сдвинулось назад от состояния истинного вакуума и в результате скатилось с энергетического холма чуть позже, чем в местах по соседству. Это вызвало появление небольшого уплотнения, которое позднее развилось в нашу галактику. Подобные же небольшие сгущения на однородном фоне распределения плотности породили соседнюю с нами Туманность Андромеды и бесчисленное множество других галактик как внутри нашего горизонта, так и за его пределами. Это описание формирования структур предполагает, что самые далекие части Вселенной более или менее похожи на то, что окружает нас здесь. Однако у меня стало возникать подозрение, что в этой картине чего-то недостает.
Влияние квантовых флуктуации крайне невелико, поскольку они намного уступают силе, тянущей скалярное поле вниз по склону энергетического холма. Вот почему поле везде одновременно достигает нижней точки, и возникают лишь очень небольшие возмущения плотности. Однако я задался вопросом: что случится, если поле находится у вершины холма, где уклон очень маленький? Здесь оно будет отдано на милость квантовых флуктуации, толкающих его случайным образом то в одну, то в другую сторону. Вселенная, возникающая после инфляции, может в результате оказаться куда менее упорядоченной и более разнообразной, чем казалось на первый взгляд.
Для описания поведения скалярного поля у вершины холма мы используем неполиткорректную, но весьма уместную аналогию. Позвольте представить вам джентльмена, назовем его мистер Филд, который слишком много выпил и теперь пытается сохранить вертикальное положение. Он плохо контролирует свои ноги, не представляет, куда направляется, и поэтому шагает то влево, то вправо совершенно случайно. Мистер Филд начинает свою прогулку с вершины холма, как показано на рисунке 8.1. Поскольку в среднем он одинаково часто шагает и вправо, и влево, ему не удастся слишком быстро куда-то уйти. Но после большого числа шагов он рано или поздно отойдет от вершины. Наконец, приблизившись к более крутой части склона, он неизбежно поскользнется и закончит путь, скатываясь вниз на пятой точке.

Рис. 8.1. Мистер Филд случайным образом блуждает по плоской части холма и соскальзывает вниз, оказавшись на крутом склоне.
Скалярное поле во время инфляции ведет себя очень похоже. Оно бесцельно блуждает вблизи вершины энергетического холма, пока не достигает крутого склона; тогда оно "скатывается" вниз, чем и заканчивается инфляция. На плоском участке вблизи вершины холма вариации поля вызываются квантовыми флуктуациями и совершенно случайны, в то же время скатывание по склону происходит упорядоченно и предсказуемо и лишь слегка возмущается флуктуациями. Интервалы времени между последовательными флуктуациями примерно равны инфляционному времени удвоения. Это означает, что мистер Филд за такой период успевает сделать лишь один шаг. Поскольку, блуждая по плоской вершине холма, он делает много шагов, это означает, что ложный вакуум, прежде чем распасться, успевает многократно удвоиться.
Конкретная последовательность шагов, приводящая мистера Филда с вершины холма к его подножию, представляет одну из возможных историй скалярного поля. Однако квантовые флуктуации, испытываемые полем, различаются от одной точки к другой, и поэтому истории скалярного поля тоже будут различными. Каждая флуктуация воздействует на небольшой участок пространства. Его размер примерно равен расстоянию, проходимому светом за один интервал инфляционного удвоения; мы будем называть этот размер "кикспэном". Можно представить себе целую группу джентльменов в таком же состоянии, как мистер Филд, каждый из которых представляет скалярное поле в некоторой точке пространства. Когда две точки находятся в пределах кикспэна друг от друга, они испытывают одинаковые квантовые флуктуации, так что соответствующие два джентльмена делают все шаги синхронно, как пара чечеточников. Но точки быстро удаляются друг от друга из-за инфляционного расширения Вселенной, и, когда расстояние между ними превысит кикспэн, компания из пары джентльменов распадется и они станут шагать независимо. Как только это случится, значения скалярного поля в двух точках начнут постепенно расходиться, а расстояние между ними продолжит стремительно расти за счет инфляции.
Малость флуктуации плотности в наблюдаемой нами области пространства говорит о том, что эта область лежала в пределах кикспэна, когда скалярное поле уже вовсю катилось вниз с холма. Вот почему эффект квантовых флуктуации был очень мал, а поле почти всюду достигло нижней точки почти одновременно. Но если бы мы могли перемещаться на очень большие расстояния, много больше горизонта, то увидели бы области, которые были в общей компании, когда поле еще блуждало у вершины холма. Истории скалярного поля в таких областях могут очень сильно отличаться от нашей, и я хотел узнать, как выглядит Вселенная на таких сверхгигантских масштабах.
Представьте себе огромную толпу пьяных людей, которые начинают расходиться с вершины холма. Каждый выпивоха представляет отдаленный регион Вселенной, так что все они движутся независимо. Если плоская часть холма имеет протяженность N шагов, то средний джентльмен пересечет ее, сделав N2 шагов. Примерно половина сделает это быстрее, а другая половина — медленнее. Например, если дистанция составляет 10 шагов, то в среднем потребуется 100 случайных шагов, чтобы ее преодолеть. Так что после 100 шагов примерно половина толпы достигнет своей конечной точки у подножья холма, а половина все еще будет наслаждаться прогулкой. Еще через 100 шагов число гуляющих вновь уполовинится, и так далее, пока последний из друзей не сверзится наконец вниз.
Но теперь заметим, что между пьяницами и расширяющимися областями пространства, которые они символизируют, есть важнейшее различие. Пока наш джентльмен шатается у вершины холма, соответствующая область пространства подвергается экспоненциальному инфляционному расширению. Поэтому число независимо развивающихся областей быстро увеличивается, как если бы наши пьяные джентльмены быстро размножались. По мере того как я размышлял об этом, картина постепенно обретала форму.
Вечная инфляция
Инфляция в известном смысле похожа на размножение бактерий. Есть два конкурирующих процесса: воспроизведение бактерий в результате деления и их эпизодическое уничтожение антителами. Исход зависит от того, какой процесс окажется эффективнее. Если бактерии уничтожаются быстрее, чем размножаются, все они скоро умрут. Напротив, если размножение идет быстрее, бактерии быстро размножатся (рис. 8.2).

Рис. 8.2. Число бактерий быстро растет, если они размножаются быстрей, чем уничтожаются.
В случае инфляции два конкурирующих процесса — это распад ложного вакуума и его "воспроизведение" в результате расширения инфлирующих областей. Эффективность распада можно охарактеризовать периодом полураспада — временем, в течение которого распадается половина ложного вакуума, если бы он не расширялся. (В нашей аналогии со случайным блужданием это время, за которое число гуляющих сокращается вдвое.) С другой стороны, эффективность воспроизведения задается временем удвоения, за которое объем расширяющегося ложного вакуума увеличивается в два раза. Объем ложного вакуума будет сокращаться, если период полураспада короче времени удвоения, и расти — в противном случае.
Однако из обсуждения в предыдущих главах ясно, что период полураспада велик по сравнению с временем удвоения. Причина этого в том, что в моделях инфляции энергетический холм весьма пологий, и нужно много шагов, чтобы его пересечь. Поскольку каждый шаг случайного блуждания соответствует одному периоду удвоения в ходе инфляции, период полураспада должен быть много больше времени удвоения. Отсюда вытекает, что области ложного вакуума размножаются намного быстрее, чем распадаются. А значит, во Вселенной в целом инфляция никогда не заканчивается и рост объема инфлирующих областей продолжается беспредельно!
В этот самый момент какие-то отдаленные части Вселенной заполнены ложным вакуумом и испытывают экспоненциальное инфляционное расширение. Но вместе с тем постоянно возникают области, подобные нашей, где инфляция закончилась. Они образуют "островные вселенные" в море инфляции.
Из-за инфляции пространство между этими островами быстро расширяется, создавая место для рождения все новых островных вселенных. Таким образом, инфляция — это процесс, идущий вразнос, который остановился в наших окрестностях, но продолжается в других частях Вселенной, заставляя ее расширяться в бешеном темпе, постоянно выметывая новые островные вселенные, подобные нашей.
Энергия распада ложного вакуума зажигает горячий огненный шар из элементарных частиц, запускает процесс образования гелия и все последующие события стандартной космологии Большого взрыва. Таким образом, момент окончания инфляции играет в этом сценарии роль Большого взрыва. Если их отождествить, то нам уже не надо считать Большой взрыв одномоментным событием в нашем прошлом. Множество таких взрывов отгремело до него в отдаленных частях Вселенной, и бессчетное число других еще произойдет повсюду в будущем.
Едва в голове у меня сложилась эта новая картина мира, я уже изнемогал от желания поделиться ею с другими космологами. И кто бы мог лучше подойти на роль моего первого конфидента, чем сам мистер Инфляция — Алан Гут, чей офис в МТИ (Массачусетский технологический институт) был всего в двадцати минутах езды от Тафтса? Так что я просто сел в машину и поехал в знаменитый институт на встречу с Аланом.
МТИ занимает громадный комплекс сооружений, где я не раз безнадежно терялся. Можно идти по коридору третьего этажа корпуса шесть и вдруг обнаружить, что уже находишься на четвертом этаже корпуса шестнадцать. Я решил не рисковать и выбрал простейший, хотя и самый длинный путь к цели — через главный вход (выделяющийся рядом коринфских колонн и увенчанный сверху зеленым куполом). Пройдя весь Бесконечный Коридор и поднявшись на несколько лестничных пролетов, я в итоге достиг офиса Гута.
Я рассказал Алану о случайном блуждании скалярного поля и о том, как описать его математически. И тут, в самой середине описания моей новой поразительной картины мира, я заметил, что Алан стал засыпать. Много лет спустя, узнав его получше, я понял, что он вообще очень сонлив. Мы организовали совместный семинар для космологов Бостона и окрестностей, и на каждом заседании Алан мирно засыпал спустя несколько минут после начала доклада. Удивительным образом, когда выступление заканчивалось, он просыпался и задавал самые глубокие вопросы. Алан отрицал наличие у него каких бы то ни было сверхъестественных способностей, но не все в это верили.
Оглядываясь назад, я понимаю, что должен был продолжать, но в то время, не зная о волшебной способности Алана, я быстро закруглился. Другие коллеги в своих отзывах тоже не проявляли энтузиазма. Физика — это наблюдательная наука, говорили они, так что мы должны воздерживаться от утверждений, которые не допускают проверки. Невозможно наблюдать ни другие большие взрывы, ни отдаленные области, где продолжается инфляция. Все они лежат за нашим горизонтом, и как нам убедиться в их реальном существовании? Я был сильно разочарован таким холодным приемом и решил включить эту работу в качестве раздела в статью по другой теме, посчитав, что она не заслуживает отдельной самостоятельной публикации.
Для объяснения идеи вечной инфляции в этой статье я использовал аналогию прогулки пьяницы у вершины холма. Пару месяцев спустя мне пришло письмо от редактора, в котором говорилось, что статья принята, за исключением того, что обсуждение пьяниц "неприемлемо для такого солидного журнала как The Physical Review", и я должен заменить его более подходящей аналогией. Я слышал, что подобный инцидент произошел ранее с Сиднеем Коулманом. В его статье была диаграмма, которая выглядела как кружок с волнистым хвостиком. Коулман называл ее "диаграммой-головастиком". Как вы уже поняли, редактор счел и этот термин неприемлемым. "О'кей, — ответил Коулман, — давайте назовем ее диаграммой-сперматозоидом". В итоге без дальнейших комментариев была принята исходная версия статьи. Я прикинул возможность применить тактику Коулмана, но в итоге отказался от нее — не хотелось ввязываться в драку.
Я не возвращался к теории вечной инфляции почти 10 лет. Если не считать одного эпизода...
Мгновение вечности
Я переключился на работу, связанную с другими моими научными интересами, и постепенно мне самому стало казаться странным, что я был так одержим ненаблюдаемыми мирами. Но, по правде сказать, соблазн бросить взгляд за горизонт Вселенной никуда не девался. В 1986 году, не в силах ему больше противиться, мы с моим аспирантом Мукундой Арьялом (Mukunda Aryal) разработали компьютерную модель вечной инфляционной Вселенной.
Мне трудно даются технологии, и я в жизни не написал ни единой строчки программного кода. Но я очень хорошо понимаю, как "думают" компьютеры, и руководил несколькими крупными вычислительными проектами моих аспирантов. Поскольку я не мог проверять их код (а даже если б мог, не думаю, что это доставляло бы мне хоть какое-то удовольствие), я всегда опасался скрытых ошибок и относился к получаемым результатам с большой осторожностью. Поэтому я заставил Мукунду выполнить множество проверок, запуская моделирование для тривиальных случаев, где мы знали ответ заранее. Наконец, убедившись, что все работает отлично, мы приступили к настоящей работе.
Моделирование началось с маленького участка ложного вакуума, представленного светлым прямоугольником на экране компьютера. Спустя некоторое время стали появляться первые темные островки истинного вакуума. По мере того как границы этих островных вселенных продвигались в море инфляции, они быстро росли в размерах. Однако инфлирующая область расширялась еще быстрее, так что интервалы, разделяющие островные вселенные, увеличивались, а во вновь образованном пространстве возникали новые островные вселенные.
На картине, открывшейся после некоторого времени моделирования, были видны крупные островные вселенные, окруженные меньшими, вокруг которых располагались еще меньшие, и так далее. Это напоминало вид архипелага с самолета — узор, который математики называют фрактальным. На рис. 8.3 показан результат похожего, но более сложного моделирования, выполненного позднее моими студентами Виталием Ванчуриным и Сергеем Виницким (Vitaly Vanchurin and Serge Winitzki).
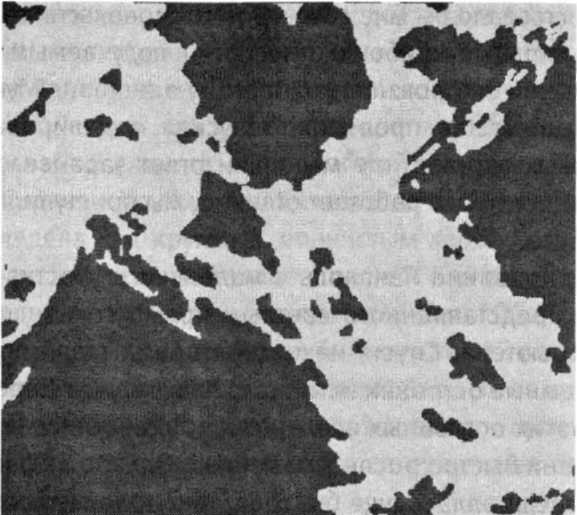
Рис. 8.3. Смоделированная на компьютере Вселенная с вечной инфляцией. Островные вселенные (темные) на фоне инфляционно раздувающегося ложного вакуума (светлого). Более крупные островные вселенные — самые старые: у них было больше времени для роста.
Мы с Мукундой опубликовали результаты моделирования в европейском журнале Physics Letters. Мое любопытство в отношении ненаблюдаемых вселенных теперь было удовлетворено и я переключился на другие работы. А данным вопросом тем временем вплотную занялся Андрей Линде.
Хаотическая инфляция Линде
Линде — настоящий герой инфляции, человек, который спас теорию посредством изобретения приплюснутого энергетического холма для скалярного поля. С 1983 года он работал над идеей о том, что Вселенная начинается из состояния первичного хаоса. Скалярное поле в этом состоянии беспорядочно меняется от точки к точке. В некоторых областях оно оказывается на вершине энергетического холма, и в таких местах происходит инфляция.
Линде понял, что полю не обязательно стартовать в верхней точке энергетического ландшафта. Оно может начинать скатываться вниз и с какой-то другой точки на склоне. Фактически энергетический холм может и не иметь верхней точки, вздымаясь ввepx без ограничений (рис. 8.4). У такого лишенного вершины — так сказать, топлес — холма есть дно — истинный вакуум, но нет определенного места для ложного вакуума. Его роль может играть любая точка на склоне, куда поле попало в исходном хаотическом состоянии, лишь бы это было достаточно высоко чтобы обеспечить необходимое для инфляции время скатывания. Линде описал эти идеи в статье, озаглавленной "Хаотическая инфляция".
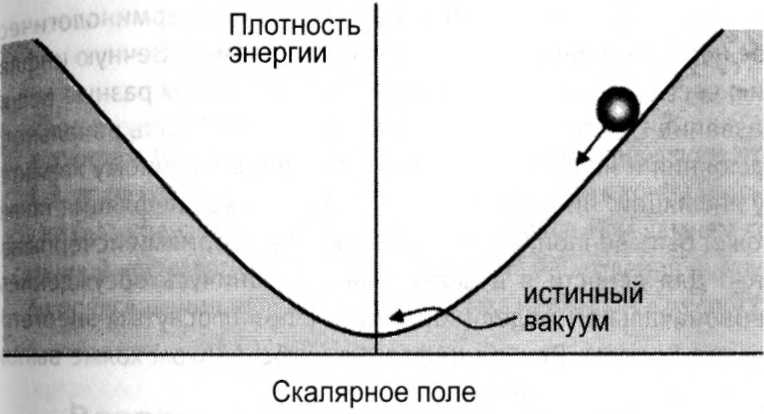
Рис. 8.4. Скалярное поле скатывается со склона "безверхого" энергетического холма.
Еще через несколько лет Линде изучил влияние квантовых флуктуаций на скалярное поле в данном сценарии. Неожиданно оказалось, что они тоже могут приводить к вечной инфляции, несмотря даже на то, что у энергетического холма нет плоской вершины.
Ключевое наблюдение Линде заключалось в том, что на больших высотах квантовые флуктуации становятся сильнее и могут толкать поле вверх против сил, тянущих его вниз по склону. Так что, если поле стартует высоко, оно не обращает большого внимания на склон и совершает случайные блуждания, как если бы находилось на вершине холма. Когда блуждания заносят его в низины энергетического ландшафта квантовые флуктуации слабее, поле начинает упорядоченно катиться вниз к состоянию истинного вакуума. Чтобы это случилось, требуется намного больше времени, чем на инфляционное удвоение, так что расширяющиеся области размножаются быстрее, чем распадаются, что опять же приводит к вечной инфляции.
Здесь я должен остановиться и прояснить терминологическое недоразумение, связанное с данной темой. Вечную инфляцию часто путают с хаотической, хотя это совсем разные вещи. Название "хаотическая" указывает на случайность начального состояния и не имеет никакого отношения к вечному характеру инфляции. Линде показал, что хаотическая инфляция также может быть вечной, но этим связь между теориями исчерпывается. Для ясности я в дальнейшем ограничусь обсуждением первоначальной модели инфляции с приплюснутым энергетическим холмом. Вечная инфляция на безверхом холме выглядит похожим образом.
Статья Линде о вечной инфляции вызвала не больше энтузиазма, чем моя, опубликованная тремя годами раньше. Однако его реакция была иной. Он не сдавал позиций, продолжал исследования по данному направлению и неоднократно выступал с докладами о своих результатах. Тем не менее физическое сообщество не поддавалось его нажиму. Понадобилось почти двадцать лет, чтобы удача повернулась лицом к вечной инфляции.
Назад: Глава 7 Антигравитационный камень
Дальше: Глава 9 Говорящие небеса

