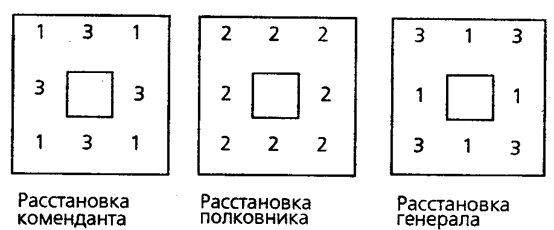
1) Эта задача решается просто: нужно переставлять часовых из середины бастиона на его углы, как показано на следующих рисунках:

2) К сожалению, здесь простой и наглый обман. Путешественники действительно заплатили 27 руб. Но это и все, никаких 30 руб. уже нет! Из этих 27 руб. хозяйка взяла себе 25 руб. и 2 руб. осталось у мальчика. На каком основании к этим 27 руб. я добавляю еще 2 руб.? Откуда я их взял? Где они? И деньги хозяйки, и деньги мальчика уже посчитаны – они в уплаченных 27 руб. Я выдумал эти 2 руб., чтобы ввести вас в заблуждение.

3) Для решения этой задачи достаточно несложных арифметических действий. Если Иван отдаст 1 овцу Петру, то овец у них станет поровну. Это позволяет нам составить равенство: овцы Петра + 1 = овцы Ивана – 1. Отсюда мы легко заключаем, что у Ивана на 2 овцы больше. Дальнейшее в том же духе. Ответ: у Петра было 3 овцы, у Ивана – 5.

4) Не знаешь, с чего начать. Но есть одна зацепка, помогающая размотать клубок. Карасев сказал: «Если вы спросите у Щукина о его профессии, он ответит, что он маляр». И Щукин действительно сказал, что он маляр! Значит, Карасев хотя бы одну правду сказал, следовательно, он не может быть вором, который всегда лжет. Может быть, Карасев – соучастник, который иногда говорит правду, а иногда лжет? Тогда вором и честным человеком должны быть Щукин и Окунев, и их ответы должны полностью отличаться один от другого, так как один из них всегда говорит правду, а другой постоянно лжет. Нет, такого не получается: ответы Щукина и Окунева в одном пункте совпадают. Следовательно, только Карасев может быть честным человеком и все, что он сказал, – правда. Ответы Окунева в одном пункте совпадают с ответами Карасева, следовательно, Окунев – соучастник преступления. И естественно, Щукин не может быть никем иным, как вором.

5) Обозначим студентов буквами A, B, C и поставим себя на место A. Он рассуждает так: «Я вижу перед собой две белые шапки. Значит, на мне белая или черная шапка. Если на мне черная шапка, то B видит перед собой черную и белую шапки. Но B ведь тоже рассуждает: „Если бы на мне была черная шапка, то C видел бы перед собой две черные шапки и сразу же догадался бы, что на нем самом белая шапка. Но C молчит, значит, на мне – белая шапка“. Таким образом, – продолжает рассуждать A, – если бы на мне была черная шапка, то B уже догадался бы, что на нем самом должна быть белая шапка. Но B молчит. Значит, он не видит на мне черной шапки. Следовательно, на мне – белая шапка!» Так рассуждал каждый из них, а поскольку все студенты соображали одинаково быстро, они одновременно решили задачу.

6) Здесь важна логика рассуждения, приводящего к решению. Нужно двигаться с конца к началу. В конце осталось 8 картофелин, что равно 2/3 того количества, которое обнаружил в чугунке третий крестьянин. Значит, всего он обнаружил 12 штук. Но это равно 2/3 того количества, которое нашел второй крестьянин. Значит, там было 18 штук. Опять-таки, это равно 2/3 того количества картофеля, которое обнаружил первый крестьянин. Следовательно, первый нашел в чугунке 27 картофелин. Столько картофелин сварила хозяйка. Первый съел 9 штук и больше ни на что претендовать не может. Второй съел 6 штук, и ему еще полагается 3 картофелины. Третий съел всего 4 штуки и должен получить еще 5 картофелин.

7) Эта задача сложная, боюсь, не все с ней справились. Действительно, 17 не делится ни пополам, ни на три части, ни на девять частей. Но вы помните: мудрец приехал, он приехал на осле! Добавив своего осла к ослам братьев, он получил 18 ослов. Половину, т.е. 9 ослов, он отдал старшему брату; третью часть, 6 ослов, он отдал среднему брату и девятую часть – двух ослов – передал младшему. Итак: 9 + 6 + 2 = 17. После этого он сел на своего осла и уехал.