Разделительно-категорический силлогизм есть умозаключение, в котором одна посылка является разделительным суждением, а вторая посылка и вывод – простыми категорическими суждениями.

Например, просыпаетесь вы утром и, еще лежа в постели, начинаете рассуждать: «Сегодня днем я могу пойти на свидание или на занятия. Пойду-ка я на свидание. Следовательно, на занятия я не пойду». Здесь первая посылка вашего рассуждения представляет собой разделительное суждение «Я могу пойти на свидание (A) или пойти на занятия (B)», символически: A v B. Вторая посылка утверждает одну из возможностей, указанных в разделительной посылке: «Я пойду на свидание» (A). Вывод отрицает вторую возможность: «Следовательно, я не пойду на занятия» (Не-B). Ясно, что вы можете рассуждать и несколько иначе: «Нет, на свидание я не пойду. Следовательно, я пойду на занятия». Символически эти два способа рассуждения можно представить следующим образом:

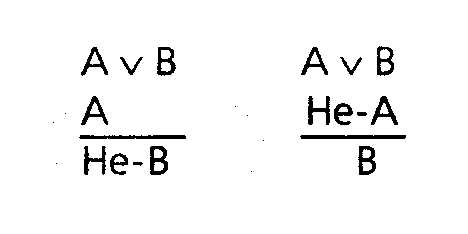
Они называются модусами разделительно-категорического силлогизма. Первый модус называется утверждающе-отрицающим, второй – отрицающе-утверждающим. Оба модуса могут приводить как к верным, так и к ошибочным заключениям. Для того чтобы не совершать ошибок при рассуждениях, имеющих вид разделительно-категорического силлогизма, нужно выполнить требование к разделительной посылке. При утверждающе-отрицающем модусе разделительная посылка должна быть строго разделительной, т.е. альтернативы должны исключать друг друга. Если это требование не соблюдено, вывод может оказаться ошибочным. Например, встречаете вы знакомого, идущего с дамой, и думаете: «Эта дама ему мать или жена». Выясняется, что дама приходится ему женой. «Ага, – делаете вы вывод, – значит, она ему не мать». Это – утверждающе-отрицающий модус, и его разделительная посылка является строго разделительной. Вывод вполне достоверен.

Но вот другой случай. Вы видите вашего знакомого, с изможденным видом бредущего по улице. «Он болен или беден», – думаете вы. Выясняется, что ваш знакомый давно и неизлечимо болен. «Значит, он не беден», – делаете вы вывод. Увы, разделительная посылка не является строго разделительной: болезнь и бедность отнюдь не исключают друг друга, особенно в наше время. Вывод может оказаться ошибочным.

Для отрицающе-утверждающего модуса требование таково: разделительная посылка должна быть исчерпывающей, т.е. должна охватывать все возможности, существующие в данной области рассуждений. В противном случае вывод может оказаться неверным.

Логическая структура именно этого модуса часто лежит в основе многих детективных сюжетов и реальной следственной практики. Совершено преступление, и следователь очерчивает круг возможных участников преступления. Дальнейшая его работа или развитие сюжета заключаются в том, что он проверяет подозреваемых и по одному отсеивает их: этот был болен, тот сидел в тюрьме в момент совершения преступления, того видели несколько человек в другом месте и т.д. Кто останется – тот и преступник. Это и есть отрицающе-утверждающий модус: преступление мог совершить A или B; A не мог совершить преступления, следовательно, его совершил B.

Хорошо, если в разделительной посылке перечислены все возможные участники преступления. А если нет? Осуждают B, а через некоторое время выясняется, что следствие упустило из виду некоего C, который и является подлинным преступником: в разделительной посылке рассуждения были учтены не все возможности. Ошибся следователь, мог ошибиться и суд. Поэтому сначала нужно доказать, что разделительная посылка является исчерпывающей, и только потом делать вывод. Тогда он будет вполне достоверным.

Конечно, в повседневной жизни и в профессиональной деятельности мы не ограничиваемся теми простыми выводами, с которыми познакомились. Мы можем соединять и комбинировать их самыми разнообразными способами, например, в одном рассуждении можно соединить условно-категорический и разделительно-категорический силлогизмы, тогда мы получим то, что называют дилеммой:

Если пойдешь направо, коня потеряешь. Если пойдешь налево, голову потеряешь. Но нужно идти направо или налево. Придется потерять коня или голову.

Но сложные комбинации умозаключений можно разложить на их простые формы и, таким образом, проверить правильность наших рассуждений.

6) Зашли как-то три крестьянина на постоялый двор. Попросили они хозяйку сварить им чугунок картофеля, а сами повалились спать. Хозяйка сварила картофель и поставила чугунок на стол.

Проснулся один крестьянин, посчитал количество картофелин и съел ровно 1/3 часть. После этого он опять улегся спать. Проснулся другой крестьянин, посчитал картофелины и, думая, что никто еще не ел, съел ровно 1/3 часть. И тоже лег досыпать. Наконец, проснулся третий крестьянин, посчитал количество картофелин и, думая, что никто еще не ел, съел ровно 1/3 часть. Тут проснулись и его товарищи. Заглянули в чугунок, а там осталось всего 8 картофелин.

Спрашивается: сколько всего картофелин сварила хозяйка? Сколько штук съел каждый крестьянин? Сколько еще должен съесть каждый крестьянин, чтобы всем досталось поровну?

7) Жил-был один дехканин, и было у него 17 основ и 3 сына. Умирая, он завещал поделить ослов между сыновьями таким образом: 1/2 – старшему сыну; 1/3 – среднему и 1/9 – младшему. Кинулись братья делить наследство, да что-то никак не получается: не рубить же осла на части! Позвали судью на помощь, но и тот ничего не смог придумать. Кто-то посоветовал братьям обратиться за помощью к одному мудрому старцу, живущему в соседней деревне. Тот приехал, разделил ослов между братьями так, как завещал отец, и уехал, провожаемый благодарностями.

Как сумел мудрец выполнить завещание отца?