Книга: Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риском
Назад: 3. Поведение портфелей с множеством активов
Дальше: Моделирование поведения простых портфелей
Дядюшка Фред делает вам еще одно предложение
Время бежит. Вы еще несколько лет проработали на дядюшку Фреда, и ежегодные сессии с подбрасыванием монеты стали вызывать у вас ужас. Законы вероятности сослужили вам хорошую службу, позволив получить равное количество «орлов» и «решек». К сожалению, ваш успех и трудовой стаж означают, что ставки при каждом подбрасывании монеты неуклонно растут. Помните, что в конце каждого года дядюшка Фред добавляет $5000 к вашему пенсионному счету и определяет подбрасыванием монеты, получили ли вы по всему счету доходность в размере 30 % («орел») или убыток в размере 10 % («решка»). Растущая сумма денег приходит в движение при каждом подбрасывании монеты, и ваш дядя ощущает ваш растущий дискомфорт.
Он делает вам другое предложение. В конце каждого года он будет делить ваш пенсионный счет на две равные части и подбрасывать монету отдельно для каждой половины.
Что же замышляет ваш хитрый дядя? Сначала вы инстинктивно отпрянете от него в ужасе: если одно подбрасывание монеты лишает вас присутствия духа, то два, безусловно, будут делать еще хуже. Однако у вас аналитический склад ума, и вы начинаете анализировать его предложение. Вы понимаете, что при двух подбрасываниях монеты существует четыре возможных результата, причем каждый выпадает с равной вероятностью.
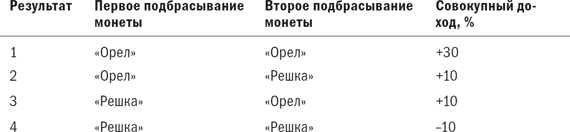
Результаты 1 и 4 – такие же, какие могли бы быть получены при однократном подбрасывании монеты с изначальной доходностью +30 % и –10 % соответственно. Однако существует два дополнительных возможных результата, при которых на два подбрасывания выпадает один «орел» и одна «решка». Совокупный доход в этих случаях равен 10 % (половина +30 % плюс половина –10 %).
Поскольку каждый из четырех возможных результатов равновероятен и за репрезентативный четырехлетний период вы получите каждый результат по одному разу, то выяснится, что ваш счет увеличится в следующее число раз:
1,3 × 1,1 × 1,1 × 0,9 = 1,4157
Хорошо оперируя числами, вы выясните, что ваша годовая доходность за сессию с двукратным подбрасыванием монеты составит 9,08 %, что почти на один процентный пункт выше вашей предыдущей ожидаемой доходности, составлявшей 8,17 %, при однократном подбрасывании монеты. Еще с большим изумлением вы понимаете, что ваш риск уменьшился: при сложении двух значений доходности при среднем значении 10 % вы получаете стандартное отклонение, равное лишь 14,14 %, в сравнении с 20 % при однократном подбрасывании монеты.
Старый мудрый дядюшка Фред объяснил вам наиболее важную концепцию теории портфелей:
Составление вашего портфеля из активов с некоррелированными результатами увеличивает доходность при одновременном уменьшении риска.
Это выглядит неправдоподобно хорошо. Ключевое слово здесь – «некоррелированные»; результат первого подбрасывания монеты никак не влияет на результат второго подбрасывания. Подумайте об этом: если бы два подбрасывания монеты были идеально скоррелированными и второе подбрасывание монеты всегда давало бы тот же результат, что и первое, то мы бы получали только изначальные +30 % и –10 % дохода.
Математические подробностиТе из вас, кто имеет солидное образование и опыт в сфере инвестиций, знают, что опцион «пут» на ценную бумагу или фьючерсный контракт при «короткой» продаже будет иметь слегка отрицательную корреляцию с доходностью на актив, лежащий в их основе (базисный актив. Прим. ред.). Однако в данном случае по двум позициям будут получены практически противоположные доходы, причем совокупный доход портфеля окажется почти равным нулю. Более точная формулировка: два актива с положительной доходностью не должны иметь постоянной резко негативной корреляции.
Мы вернемся к первоначальному однократному подбрасыванию монеты с его более низкой доходностью и более высоким риском. Если бы второе подбрасывание монеты имело идеальную обратную корреляцию с первым и всегда давало бы противоположный результат, то наша доходность всегда составляла бы 10 %. В этом случае мы имели бы долгосрочную годовую доходность в 10 % с нулевым риском. Важно усвоить следующее: смешение активов с некоррелированной доходностью уменьшает риск, поскольку, в то время как доходность одного актива падает, на другой актив она, вероятно, растет.
В реальном мире инвестиций иногда можно встретить два класса акций или облигаций, имеющих нулевую корреляцию, что дает увеличение доходности на один процент или около того и слегка снижает риск. Однако учтите, что в итоге значимые отрицательные (обратные) корреляции никогда не встречаются. А если бы встречались, это было бы слишком неправдоподобно.
Назад: 3. Поведение портфелей с множеством активов
Дальше: Моделирование поведения простых портфелей

