НЕОБЫКНОВЕННЫЕ ПРИКЛЮЧЕНИЯ ТЕННИСНОГО МЯЧИКА
Возражая в 1634 году Бекману, который полагал, что скорость света конечна, Декарт, убежденный, что свет распространяется мгновенно, отметил:
…Ты настолько доверяешь своим наблюдениям, что, если окажется, что нет ни малейшей задержки между испусканием и поглощением светового импульса, ты все равно будешь придерживаться своей ложной философии, я же, напротив, должен сказать, что если такая задержка будет обнаружена, то все основания моей философии будут полностью ниспровергнуты. <…>. Я столь убежден в этом (то есть в бесконечной скорости распространения света. – И.Д.), что, если будет доказана ложность этой идеи, я вынужден буду признать, что совершенно не сведущ в философии.
Спустя несколько лет, 9 февраля 1639 года, обсуждая открытие У. Гарвея, Декарт признался Мерсенну:
Если то, что я написал об этом (то есть об открытии кровообращения. – И.Д.), или же о преломлении света, или о чем-либо ином, чему я посвятил в моих опубликованных работах более трех строк, окажется ложным, все остальное в моей философии не будет иметь никакой ценности (ne vaut rien).
Нечто подобное, как мы видели, Декарт говорил и по поводу идеи движения Земли. Это не случайно. Все идеи его философии настолько тесно связаны друг с другом, образуя цельную структуру, что устранение одной из них действительно грозило обрушением всей конструкции.
Почему Декарт полагал скорость света бесконечной? По-видимому, он рассуждал следующим образом: все в его «новом мире», лишенном пустоты, реально движется по кругу или, точнее, по замкнутой траектории; хотя потенциально тела должны двигаться прямолинейно, однако «различные положения материи превращают эти [прямолинейные] движения в неправильные и криволинейные» (см. Приложение VI), и лишь свет распространяется по прямой. Следовательно, движение света – это не реальное движение с конечной скоростью, но некая актуализованная потенциальность, «склонность к движению», по выражению Декарта. «Склонность» же не может распространяться с конечной скоростью, она просто присуща материи или возникает при определенных условиях, мгновенно «охватывая» соответствующий фрагмент реальности (соответствующую протяженность).
«Вам не должно казаться странным, – пишет он в «La Dioptrique», – что лучи света могут мгновенно распространяться от Солнца до нас, ибо известно, что действие, приводящее в движение один конец палки, в одно мгновение доходит до другого и что оно должно таким же образом распространяться даже в том случае, если бы расстояние было больше, чем то, которое отделяет Землю от небес.
Декарт поясняет эту мысль на примере чана, в котором бродит виноград и в котором внизу с разных сторон сделаны два отверстия для стекания перебродившего сока (полную цитату и соответствующий рисунок из «La Dioptrique» см. в Приложении VIII).
В принципе, вся жидкость в чане имеет «склонность» (или «тенденцию») течь вниз. При этом, замечает Декарт, «необходимо делать различие между движением и действием или склонностью к движению, ибо нетрудно представить, что части вина, которые располагаются около [точки] С (см. рис. в Приложении VIII. – И.Д.), стремятся к отверстию А и в то же время к В, хотя актуально (actuellement) они не могут двигаться к обоим отверстиям одновременно…». Кроме того, «они стремятся точно по прямой линии к B и к A, несмотря на то что они не могут перемещаться строго по прямой линии из-за гроздей, находящихся между ними. Следовательно, ввиду того, что это не столько движение, сколько действие светящихся тел, которое надлежит воспринимать как свет, излучаемый ими (ce n’est pas tant le mouvement, comme l’action des corps lumineus qu’il faut prendre pour leur lumiere), вы должны прийти к выводу, что лучи света суть не что иное, как линии, вдоль которых стремится это действие. Таким образом, существует бесконечное число лучей, идущих от всех точек светящихся тел ко всем точкам, освещаемым ими, точно так же как имеется беспредельное количество прямых линий, вдоль которых действие, распространяющееся от поверхности винограда CDE, стремится к A; существует безмерное множество и других линий, вдоль которых действие, идущее от тех же точек, стремится к B, причем эти действия, или стремления, не мешают друг другу». Замечу, что Декарт постоянно использует такие термины, как tendre (в значении: иметь склонность, тенденцию, стремиться к чему-либо), inclination и т.п., которые, строго говоря, нельзя признать удачными для философа, поставившего себе целью изгнать из мира протяженных сущностей всякие «стремления», «склонности», «тенденции» и прочие «тени мысли».
Между тем метафизическую идею бесконечной скорости света следовало далее конкретизировать в некой, как бы мы сейчас сказали, модели, что Декарт и делает.
Напомню, что в картезианской натурфилософии частицы второго элемента имеют шарообразную форму. Кроме того, всякая составная часть вихря «отбрасывается» вихревым движением от центра вихря к периферии, подобно камню в праще. Давление центрального ядра вихря, состоящего из первого элемента, распространяется по всему вихрю прямолинейно к его периферии, действуя также и на соседние вихри. Вещество первого элемента, поступающее из соседнего вихря, оказывает давление на периферию данного вихря, наполненную шарообразными частицами второго элемента. Свет распространяется мгновенно от одного «шарика» к другому в виде давления. Это давление ощущается глазом в форме света, а световые лучи, по Декарту, как уже было сказано, есть не что иное, как линии, по которым распространяется действие. Каждое светящееся тело действует подобным образом, потому что оно вследствие быстрого движения своих продолговатых мельчайших частиц постоянно давит и толкает окружающие его шарики второго элемента. Нельзя сказать, что эта картезианская модель отличается «ясностью и отчетливостью», но самое любопытное начинается далее, когда философ переходит к рассмотрению конкретного явления, скажем, преломления света. Его рассуждения при этом совершенно меняют свой характер.
Прежде всего Декарт, не исследуя никаких реальных оптических явлений, обращается к аналогии движения света с движением теннисного мяча. При этом он исходит из следующих идеализаций: во-первых, следует допустить, что плоская поверхность, о которую ударяется мяч, абсолютно гладкая и твердая; во-вторых, следует абстрагироваться от таких параметров мяча, как вес (в данном контексте этот термин используется как синоним термина «масса»), размер и форма, поскольку эти характеристики могут играть важную роль в движении мяча, но не света. Таким образом, Декарт идет по «скользкому пути абстракций (slippery path of abstraction)», как выразился У. Шей, несколько дальше, чем основоположники классической механики от Галилея до Эйлера, ибо последние, оперируя идеализированным объектом, называемым ныне «материальной точкой», допускали, что этот объект массу, а потому и вес, все-таки имеет, тогда как Декарт, желая «подогнать» свойства моделирующего объекта под свойства изучаемого, от этой характеристики отвлекается.
И наконец, еще об одном важном допущении, сделанном Декартом, необходимо упомянуть. Обсуждая столкновение мяча с твердой и гладкой плоской поверхностью, он полагает:
…Стремление к движению по некоторому направлению, подобно самому движению и, вообще говоря, любой другой величине, может быть разбито на все составляющие, какие только можно вообразить; нетрудно представить себе, что скорость мяча, летящего из A в B [рис. 3.8], делится на две составляющие, одна из которых заставляет его спускаться с линии AF к линии CE, а другая одновременно вынуждает мяч переместиться от левой стороны AC к правой FE таким образом, что обе они (то есть обе указанные составляющие. – И.Д.), соединенные вместе, направляют мяч в B по прямой линии AB. Далее легко понять, что встреча мяча с поверхностью земли может изменить лишь одну из этих скоростей (то есть только одну из компонент скорости. – И.Д.), но никак не другую; так как встреча должна помешать скорости, заставляющей мяч спускаться с AF к CE вследствие того, что земля занимает все пространство, находящееся под CE, то как же она могла бы препятствовать другой скорости (то есть горизонтальной компоненте скорости. – И.Д.), побуждающей мяч перемещаться вправо, ведь она никоим образом не противостоит ему в этом направлении?
По сути, Декарт говорит здесь о двух допущениях. Первое сводится к тому, что при ударе мяча о землю изменяется только вертикальная компонента его скорости. Второе допущение более существенно: когда Декарт говорит, что «стремление к движению по некоторому направлению, подобно самому движению <…> может быть разбито на <…> составляющие», он имеет в виду мысль, сформулированную им в предыдущей главе «La Dioptrique»: «легко поверить, что действие или стремление к движению, о которых я сказал, что их следует принимать за свет, должны следовать тем же законам, что и движение». «Нет, месье Декарт, – мог бы возразить внимательный читатель, – не легко и очень даже не легко поверить, что нечто (как вы там его ни называйте – действием или стремлением к движению), способное распространяться с бесконечной и только с бесконечной скоростью, что утверждалось всего абзацем выше, вдруг, как выясняется, следует законам движения с конечными скоростями и, как выяснится в следующей главе, может менять свою скорость». Но в тексте «La Dioptrique», как и в переписке Декарта, нет ничего, что могло бы рассеять сомнения и сделать картезианскую мысль «ясной и отчетливой». Поэтому читателю остается только продолжить знакомство с «La Dioptrique».
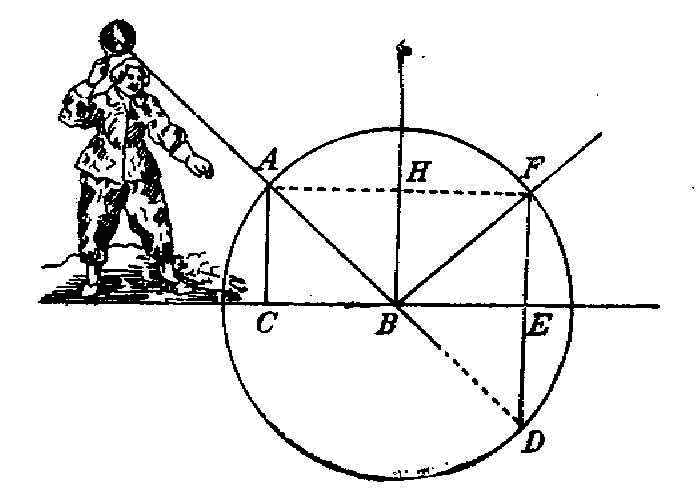
Рис. 3.8. К рассмотрению Декартом столкновения мяча с твердой и гладкой плоской поверхностью
Обращаясь к явлению преломления света, Декарт вносит в принятую им ранее аналогию с теннисным мячом новые нюансы.
Прежде всего предположим, – пишет он, – что мяч, выброшенный из A [рис. 3.9] по направлению в B, встречает в точке B не поверхность земли, а кусок материи CBE, которая настолько слаба и редка, что он может прорвать ее и пройти насквозь, теряя только часть скорости, например, половину. Если это так, то для того, чтобы знать, каким путем мяч должен следовать, примем опять во внимание, что его движение совершенно отличается от стремления к движению скорее в одну сторону, чем в другую, откуда вытекает, что их значение должно рассматриваться отдельно; учтем также, что из двух составляющих этого стремления лишь та из них, которая вынуждает мяч спуститься сверху вниз, может быть сколько-нибудь изменена при встрече с материей <…>. Далее, описав из центра B окружность AFD и начертив под прямыми углами к CBE три прямых линии AC, HB, FE таким образом, чтобы расстояние между FE и HB было в два раза больше, чем между HB и AC, мы увидим, что мяч должен стремиться к точке I; поскольку мяч, проходя через кусок материи CBE, теряет половину своей скорости, постольку он должен употребить, чтобы опуститься вниз от точки B до какой-нибудь точки окружности AFD, в два раза больше времени, чем то, которое ему понадобилось для прохождения от A к B; а так как мяч ничего не теряет из своего стремления продвигаться к правой стороне, то за удвоенное время [по сравнению с тем, которое ему потребовалось, чтобы переместиться от линии AC до линии HB] он должен проделать в эту сторону путь в два раза больший и, следовательно, достичь некоторой точки прямой FE в то же самое мгновение, когда он приближается к какой-либо точке окружности AFD; это возможно только при условии, если мяч направляется к точке I, ибо она является единственной под куском полотна CBE, где окружность AFD и прямая линия FE пересекаются.
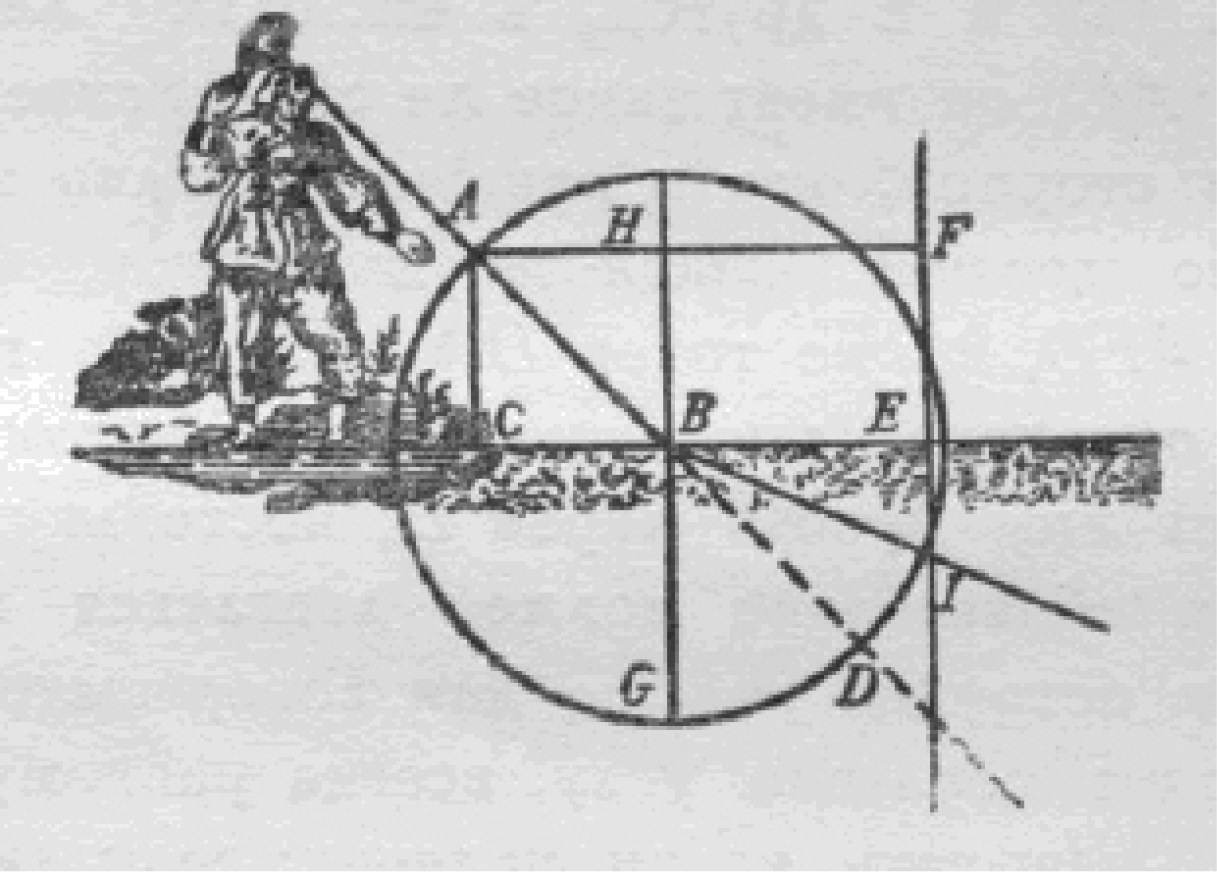
Рис. 3.9. К рассмотрению Декартом столкновения мяча с куском материи
Теперь, предлагает Декарт, заменим кусок полотна поверхностью воды, которая «отнимет у мяча» тоже половину скорости (как и в предыдущем случае). Все приведенные рассуждения при этом останутся в силе и «мяч неизбежно направится из точки B по прямой линии не к D, а к I» [рис. 3.10]. Часть воды, «заполняющей все пространство от B до I, сопротивляется то больше, то меньше по сравнению с воздухом, наличие которого мы ранее предполагали; однако это не означает, что вода должна в большей или в меньшей степени отклонить мяч, ибо она легко раздается (car il se peut ouvrir), с одинаковой легкостью открывая ему путь как в одну сторону, так и в другую, по крайней мере, если, как и ранее, исходить из предположения, что ни тяжесть или легкость мяча, ни его величина или форма, ни какая-нибудь иная причина не меняют его направления».
Описав движения мяча в разных ситуациях, Декарт обращается в анализу движения света, который, переходя из воздуха в воду (то есть из менее плотной в более плотную среду), отклоняется, но, как показывают наблюдения, в направлении, противоположном отклонению мяча, в сторону отрезка HG [рис. 3.11]. Чтобы объяснить этот факт, Декарт допустил, что мяч, «брошенный из A в B, отбрасывается снова, находясь в точке B, поверхностью CBE, увеличивающей силу его движения, например, на одну треть, таким образом, чтобы он мог потом совершить за двойной промежуток времени такой же путь, какой он проделывал за тройной; подобное действие следует рассматривать так, как если бы мяч встречал в точке B тело такого характера, что он мог бы пройти через его поверхность CBE на одну треть легче, чем через воздух. Из приведенного доказательства (sic! – И.Д.) с очевидностью вытекает, что если описать окружность AD [рис. 3.11], как было сделано ранее, и провести линии AC, HB и FE таким образом, чтобы между FE и HB было бы расстояние на треть меньшее, чем между HB и AC, то точка I, где прямая линия FE и окружность AD пересекаются, укажет место, к которому мяч, находясь в точке B, должен отклониться». Таким образом, расстояние BI определяется соотношением BE = GI = 2BC/3, и перпендикуляр FE, будучи продолжен вниз до пересечения с окружностью, пересечет ее в точке I. В итоге Декарт делает следующий вывод: «поскольку мяч, идущий по прямой линии из A в B, отклоняется в точке B и отсюда направляется к точке I, постольку это означает, что сила, или легкость, с какой он входит в тело CBEI, относится к той, с которой он покидает тело ACBE, как расстояние, отделяющее AC от HB, относится к расстоянию между HB и FI, то есть как отрезок CB относится к отрезку ВE». Последнее утверждение эквивалентно так называемому закону синусов, или, другое название, закон Снелия. Действительно, если угол ABH – это угол падения (i), а угол IBG – угол преломления (r), то поскольку sin i = AH/AB, sin r = GI/BI и AB = BI = 1, то sin i = AH = CB и sin r = GI = BE. Следовательно, CB/BE = sin i / sin r.
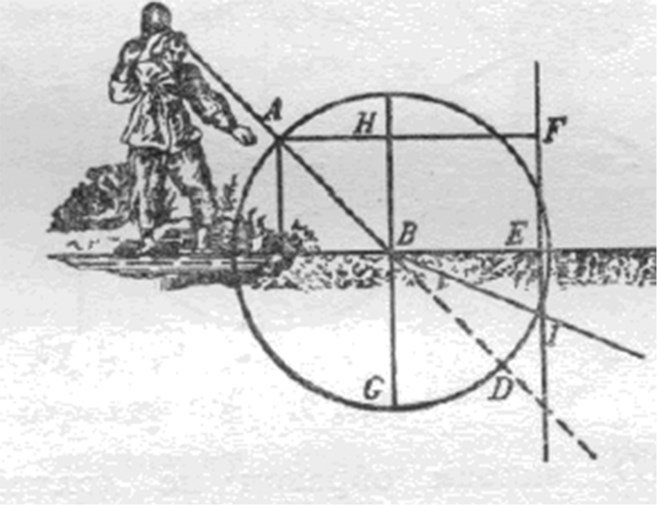
Рис.3.10. К рассмотрению Декартом столкновения мяча с поверхностью воды
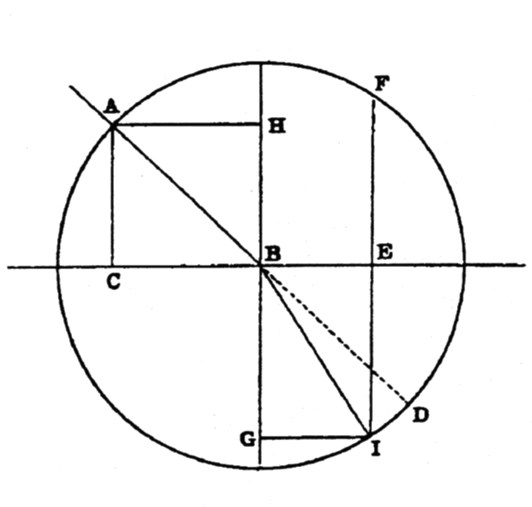
Рис. 3.11. К анализу Декартом прохождения света из воздуха в воду
А теперь вдумаемся в то, что Декарт в одной из приведенных выше цитат назвал роскошным словом «доказательство». Начну с того, что если, как это имеет место в случае преломления, скорость света при переходе из одной среды в другую изменяется, то и радиус окружности, который в построениях Декарта пропорционален скорости света (или мяча), также должен изменяться, а вместе с ним и длина отрезка CBE. В результате все построения усложняются, а при углах падения больше 30° становятся вообще бессмыcленными, поскольку в этом случае отрезок FE оказывается вне окружности, что означает отсутствие преломления света, хотя Декарт нигде не оговаривает, что при таких углах свет не преломляется. Кстати, на рисунке в «La Dioptrique», иллюстрирующем «доказательство» закона преломления, угол падения равен 44°. Но об этом рисунке речь впереди.
Утверждение Декарта, что перпендикуляр FE, будучи продолженным вниз до пересечения с окружностью (даже если забыть, что это должна быть уже другая окружность), пересечется с ней именно в точке I, следует вообще отнести к тому, что англичане называют sleight-of-hand.
Далее, – и это самое, мягко говоря, неубедительное место в его рассуждениях – Декарт полагает, будто через более плотную среду свет проходит быстрее (в его терминологии – «легче»). А аналогичное утверждение касательно мяча – ударившись о поверхность воды, мяч далее будет двигаться (в более плотной среде!) с большей скоростью, чем ранее он двигался в воздухе, поскольку-де при ударе он получит дополнительный толчок, – даже как-то неприлично комментировать (вряд ли Декарт когда-либо наблюдал ускорение камня, попавшего в песок). Ах да, совсем забыл – он же строит «новый мир», исключительно рациональный! И рассуждает при этом следующим образом: давайте, дорогой читатель, для начала вспомним «ту природу, которую я приписываю свету». Нелегкое, заметим, упражнение для читательской памяти, потому как в разных абзацах своего трактата автор приписывал свету, как мы видели, разную природу. Но Декарт приходит на помощь, напоминая, о чем именно идет речь: свет есть не что иное, как некое движение или некое действие, оказываемое на очень тонкую материю («une matière très subtile»), заполняющую поры материальных тел. Далее, автор настоятельно рекомендует читателю поверить не только в то, что мяч (покинуть теннисный корт с прудом по соседству месье де Перон не желает категорически, ведь ему обязательно нужна механическая модель, доступная средним интеллектам) теряет больше своего движения («perd advantage de son agitation»), ударяясь о мягкое (или рыхлое) тело («un cors mou»), чем сталкиваясь с твердой (или по крайней мере с более плотной) поверхностью (эта мысль сама по себе справедлива), но и в то, что, ударившись о твердую поверхность, мяч будет двигаться быстрее. Действительно, рассуждает Декарт, поры воздуха расположены неупорядоченно, постоянно меняют свою форму, размеры и местоположение, что крайне затрудняет продвижение света через заполняющую их тонкую материю, свет как бы «вязнет» в воздухе. Иное дело более плотные тела, там поры расположены упорядоченней, их размеры и форма постоянней, поэтому свету в них двигаться легче. Таким образом, скорость («легкость») распространения света в среде зависит от свойств этой среды.
У. Шей дополнил приведенные рассуждения Декарта современной аналогией:
[…Сидя за рулем автомобиля], я до отказа жму на газ, однако по мягкому грунту машина движется еле-еле, но как только колеса касаются твердого покрытия, я начинаю ехать с бешеной скоростью.
Все это остроумно и замечательно, но… теннисный мяч, попав в воду, будет там двигаться с меньшей скростью, чем в воздухе. И, конечно, следует еще раз сказать о несоответствии картезианских физических и метафизических представлений о природе света. На метафизическом уровне анализа скорость света, по Декарту, бесконечна, но когда речь заходит о физике и метафизический свет сменяется реальным, меняется и теория.
Теперь о рисунке, иллюстрирующем картезианский «вывод» закона преломления света [рис. 3.9]. Напомню, что в сопровождающем этот рисунок тексте сказано: поскольку мяч, проходя сквозь кусок материи, теряет половину своей скорости (причем изменяется только ее «вертикальная» компонента), то HF = 2AH. Однако на рисунке в «La Dioptrique» AH = 10,5 мм и HF = 14 мм вместо 21 (при AB = 15 мм). На первый взгляд пустяк. Подумаешь, гравер ошибся, немножко укоротил сторону AF. Бывает. Декарт-то здесь при чем? Кстати, сам Декарт, когда этот зануда Т. Гоббс начал замерять углы да отрезки на чертежах в «La Dioptrique», так тому (через Мерсенна) и ответил, что, мол, он, Рене Декарт, не стал исправлять эту «ошибку печатника (la faute de l’imprimeur)» потому, что уверен – «не найдется читателя настолько тупоумного (si stupide), который будет не в состоянии понять, что один отрезок должен быть вдвое больше другого».
Декарт лгал. Он был слишком хороший математик, хотя и не такого масштаба, как Пьер Ферма или Исаак Ньютон, чтобы не понять, что не в ошибке печатника тут дело (кстати, рисунки делались не типографом, а Франсом ван Схотеном под неусыпным авторским контролем). Дело в том, что если угол ABH оказывается больше 30°, то, как я уже отмечал, отрезок FE выходит за пределы окружности. Это, повторяю, означает, что при углах падения, превышающих 30°, преломление света невозможно. Декарт же признать это никак не мог, поскольку такой вывод противоречил бы опыту, и такое несоответствие с данными наблюдений было бы уже непреодолимо никакой демаго… простите, никакой метафизикой. Поэтому он в свое оправдание, свалив вину на типографа, заявил в письме Мерсенну от 20 октября 1642 года:
…Я использовал отношение 2 :1 (то есть HF = 2AH. – И.Д.)… потому, что оно простейшее и я хотел выразиться ясно, однако я отдал в печать рисунок с наименьшим [отношением], чтобы показать, что то же самое рассуждение должно распространяться на все возможные отношения (le mesme discours se doit entendre de toutes sortes de proportions), а также для того, чтобы оно (наименьшее отношение) не казалось не соответствующим опыту.
Увы, все это не имеет никакого отношения к реальности.
Таким образом, Декарт не дал никакого вывода «закона синусов», то есть закона преломления, а то, что было им предложено, – это конгломерат спорных, противоречивых, а порою и просто ошибочных умозаключений, которые «подгонялись» под известный ему заранее (оставляю в стороне вопрос «откуда?») результат.
По мнению У. Шея, Декарт был близок к открытию явления полного внутреннего отражения. Не думаю. Для этого он должен был бы в принципе изменить свой подход к рассмотрению явлений природы, я бы даже сказал жестче – для этого нужна была иная культура построения математических моделей природных явлений, у истоков которой стоял Галилей. Культура, основанная на продуманных идеализациях, а не на поверхностных аналогиях (чан с виноградом, теннисный мяч, слепец с тростью и т.д.) и риторике. У Декарта же мы видим поразительное несоответствие рационалистических методологических установок и реальной практики рассмотрения природных явлений, несоответствие, которое не бросалось в глаза только потому, что труды французского мыслителя традиционно становились предметом исследовательского внимания историков философии и философов, и лишь изредка – историков науки, не поленившихся внимательно, что называется, в карандашом в руках, шаг за шагом изучить Декартовы научные труды и высказывания.
Между тем современники Декарта, не знавшие, что имеют дело с основоположником европейского рационализма, относились к его рассуждениям и выводам весьма критически. В первую очередь следует назвать Ферма, Гоббса и Гассенди. Иезуит отец Антуан Ватье, преподаватель в коллегии Ла-Флеш с 1618 по 1642 год, прочитав «Discours de la Méthode» c приложенной к ним «La Dioptrique» и другими сочинениями, выразил изумление по поводу того, что картезианский метод обещал торжество рациональной интуиции, а на деле дал только набор эмпирических моделей. Декарт ответил, что он привел (в «La Dioptrique») доказательства a posteriori, поскольку доказательства a priori потребовали бы от него полного изложения всей его физики. Разумеется, он мог бы вывести все свои утверждения из первых принципов метафизики, но вместо этого он позволил истине самой заявить о себе. «Я хотел выяснить, – писал Декарт Ватье 22 февраля 1638 года, – достаточно ли просто провозгласить истину, чтобы быть убедительным». Однако спустя несколько дней Декарт написал Мерсенну (сообщать которому что-либо было все равно что в наши дни делать заявление по телевидению), что доказал-таки «рефракцию геометрически и a priori». Обрадованный Мерсенн, естественно, ждал подробностей, весьма неделикатно напомнив Декарту, что до сих пор тот использовал лишь модели да аналогии. Но Картезиус тут же вернулся на прежние позиции. «Требовать от меня геометрических доказательств в вопросе, касающемся физики, – писал он с возмущенным удивлением, – значит требовать от меня невозможного». Как заметил У. Шей, «Мерсенну оставалось молча восхищаться (Mersenne was left to marvel in silence…)».
Назад: ПРЕВРАТНОСТИ МЕТОДА
Дальше: РАЦИОНАЛИЗОВАННЫЙ ГЕЛИОЦЕНТРИЗМ

